Flageolet tone

Fundamental oscillation and harmonics of a string

A flageolet tone [ ˌflaʒoˈlɛttoːn ], also called flageolet for short , English (string) harmonic (abbreviation: Harm. ), Spanish armónico , is a tone or overtone usually generated on a stringed instrument , which is created by the excitation of a harmonic of the string and its frequency thus corresponds to an integer multiple of the fundamental frequency of the string. The name comes from the flageolet- like sound of these notes on the violin .

With stringed instruments such as violins or guitars, the finger is placed lightly on the string division points 1: 2, 1: 3, etc. in order to generate flageolet tones, so that only those harmonics can arise that have a vibration node at the relevant point . In contrast to firm gripping (shortening of the swinging length of the string), the string vibrates as a whole, ie also "behind" the finger (see → figures below ).

As already indicated above, flageolet tones occur mainly as “special effects” in stringed or bowed and plucked instruments (violin, viola, cello, double bass, acoustic and electronic guitar). Flageolets are also possible on other instruments, such as the piano, but they are much less common in practice.

Regarding the feasibility: the higher the flageolet, the worse it responds and the more difficult it is to produce.

Physically, flageolet tones correspond to the natural tones of wind instruments that are generated by overblowing .

Differentiation in terms of type of generation

Natural flageolet

The starting point is the open string . The sound is usually noted here , as there is usually only one possible version, or in the case of several possible versions, the choice can be left to the player. A circle is placed above it, which indicates that the corresponding tone can be produced by (natural) harmonics. If you want to note the fingering, you may have to specify the string on which the natural flageolet is to be performed. The tone of the slightly placed finger is noted as a diamond-shaped notehead.

Artificial Flageolet

The starting point is the firmly gripped string. The firmly gripped finger is noted as a normal notehead and the loosely attached finger as a diamond-shaped notehead. Often times, the actual sound is added in brackets. Artificial flageolets require a great deal of care and are more difficult to produce than natural flageolet tones due to the complex handles.

Plectrum harmonics on the guitar

This flageolet, in contrast to the natural flageolet, is mainly performed with the touch hand. If a string is played with a pick, it is immediately dampened again with the striking hand (for example with the knuckle of the thumb or the middle finger). In this way, very high flageolets can also be created. The required keynote is picked up with the other hand.

In 1962 guitarist Roy Buchanan experimented with pinchharmonics for the first time in this way .

Differentiation with regard to the interval used

Depending on the interval between the initial tone and the tone that would sound with firm grasping instead of loosely laying the finger on, the height of the flageolet tone produced at this point varies:

Octave harmonics: The harmonics in the octave (1/2 string length) produce the same pitch as if you were gripping the high note.
Fifth harmonics: If the harmonica is played a fifth above the (empty or fingered) starting note (1/3 string length), the result sounds a duodecime (= octave plus fifth) above the starting note.
Quart flageolet: If the flageolet is played a fourth above the (empty or fingered) starting note (1/4 string length), the result sounds a double octave above the starting note.
Third or sixth flageolet (large): If the harmonics are played a major third or major sixth above the (empty or fingered) starting note (1/5 or 2/5 string length), the result sounds a double octave plus a major third above the starting note.
Third flageolet (small): If the harmonics are performed a minor third above the (empty or fingered) starting note (1/6 string length), the result sounds a double octave plus a fifth above the starting note.

Special applications

Technical relief

Natural harmonics with a distance of more than an octave to the open string do not sound like the firmly gripped notes in all, but in many cases. However, since the flageolet tones “jump in” better and still sound correct even if the fingering is slightly imprecise, they are often used in difficult string passages in high registers to facilitate the playing technique.

Representation of pure intervals for fret instruments

Since the sounding pitches are part of the natural tone series , they deviate more or less from the usual equal temperament . A third positionolet, for example, sounds 14 cents lower than the firmly gripped major third . With flageolet tones, fret instruments ( guitar or viol ) can also be played in pure tuning .

Flageolet glissando

A special effect is the flageolet glissando , in which - unlike the firmly gripped glissando - not all notes, but only the overtones of the respective open string are made to sound.

A particularly impressive application of this effect can be found in Stravinski's ballet The Firebird , where it is used in the introduction to the atmospheric portrayal of the magic forest.

Tuning aid

Flageolet tones can be used well for tuning (especially lower) stringed instruments such as guitar, electric bass , cello and double bass . For this purpose, a suitable natural harmonics tone is played and compared with the fundamental tone of another, higher, open string. A deviation between the pitches is then clearly audible through beats .

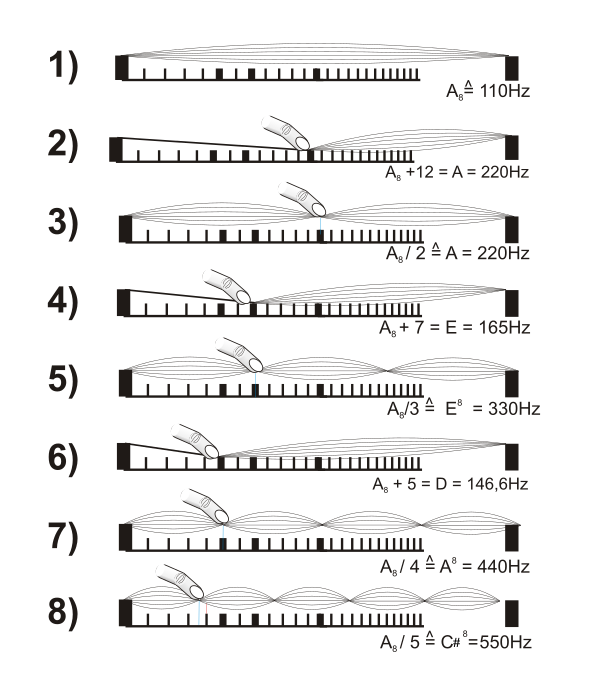
Representation of harmonics on the guitar

The following drawing shows different natural harmonics on the A string of the guitar compared to simply fingered strings.

The "calculations" are not formally correctly written down, but are simply a simplified shorthand. Additions here refer to the frets and divisions to the division ratio of the string. The numbers ₈ and ⁸ indicate octave leaps.

Web links

Wikibooks: Guitar: Voices with Flageolet - Learning and teaching materials

Flageolet excursus in Die Ärzte

Individual evidence

↑ Hermann von Helmholtz : The theory of tone sensations as a physiological basis for the theory of music . VDM Müller, Saarbrücken 2007, page 87, ISBN 978-3-8364-0606-2 (unchanged reprint of the edition F. Vieweg, Braunschweig 1870, online ).
↑ Adolf Bernhard Marx : The theory of musical composition, practically theoretical, Vol. 4 . Breitkopf & Härtel Verlag, Leipzig 1860, page 269 ( online ).
^ Hannes Fricke: Myth guitar: history, interpreters, great hours. Reclam, Stuttgart 2013, ISBN 978-3-15-020279-1 , p. 39.

[1] Hermann von Helmholtz : The theory of tone sensations as a physiological basis for the theory of music . VDM Müller, Saarbrücken 2007, page 87, ISBN 978-3-8364-0606-2 (unchanged reprint of the edition F. Vieweg, Braunschweig 1870, online ).

[2] Adolf Bernhard Marx : The theory of musical composition, practically theoretical, Vol. 4 . Breitkopf & Härtel Verlag, Leipzig 1860, page 269 ( online ).

[3] Hannes Fricke: Myth guitar: history, interpreters, great hours. Reclam, Stuttgart 2013, ISBN 978-3-15-020279-1 , p. 39.