Vibrating membrane

This article or section needs to be revised. Details should be given on the talk page. Please help to improve it , and then remove this flag.

This article or the following section is not adequately provided with supporting documents ( e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

Membrane of a subwoofer

Two-dimensional standing harmonics in a rectangular frame

Steinitz cross-flow microphone (1927)

A vibration membrane or oscillation membrane ( membrane , from Middle High German membrane "(piece) parchment "; from Latin membrana " skin " or membrum "limb") is a thin skin or film that is supposed to generate or modify vibrations .

The membrane can be used to generate, amplify, absorb, dampen or measure the vibration. The stimulation of membrane vibrations presupposes that there is a continuously acting external force , which is given by the tensile stress through an edge restraint.

Each membrane has several natural resonances ( partial vibrations ), but these are often heavily dampened . In their vicinity, the amplitudes can reach particularly high values.

meaning

Vibrating membranes play an important role in acoustics in numerous areas:

• mainly with the electroacoustic converters , where they
  • serve to convert mechanical sound energy into electrical energy , e.g. B. with the microphone , or
  • conversely to the conversion of electrical energy into sound energy, e.g. B. with speakers or headphones ,
• during the listening process
• with certain musical instruments, e.g. B. the membranophones .

Classifications

The membrane can

• be clamped in a solid frame like a drum ,
• however, its edge can also vibrate freely like a loudspeaker.

Both variants differ significantly in terms of possible modes and frequencies .

The excitation of vibrations can take place in different ways, for example

• by the impact of airborne sound , e.g. B. the eardrum ,
• by striking with a mallet , for example in the case of membranophones , or
• by electrical means, for example by stimulating a loudspeaker membrane.

A membrane is also built into the chest piece of the stethoscope .

Technical vibration diaphragms are used, for example, in pressure measuring devices , diaphragm pumps and musical instruments . The eardrum is an example of a biological vibration membrane.

Mathematical description

Oscillation of the undamped circular membrane

The oscillation of the undamped circular membrane can be described with the d'Alembert oscillation equation in polar coordinates . The rule here is that the diaphragm is clamped at the radius and thus the deflection is zero. In terms of the theory of partial differential equations , this corresponds to the homogeneous Dirichlet boundary condition . This problem can be described as follows: ${\displaystyle a}$ ${\displaystyle u}$

${\displaystyle {\frac {\partial ^{2}u}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial u}{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}u}{\partial \varphi ^{2}}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}=0\quad {\text{mit}}\quad u(a,\varphi ,t)=0\quad {\text{und}}\quad u(r,0,t)=u(r,2\pi ,t)}$

The approach to such a problem is usually a separation approach , which states that the function sought is composed of separate functions . Since the membrane is clamped at the edge, primarily only certain forms of oscillation are possible, the natural oscillations (also called modes). However, by superposing these natural oscillations, other oscillation forms can also be represented. ${\displaystyle u(r,\varphi ,t)}$ ${\displaystyle f(r),g(\varphi ),h(t)}$

In the case of cylinder or circle geometries, the solution is composed on the one hand of complex exponential functions (or trigonometric functions ) and on the other hand of the cylinder functions (also called Bessel functions ). The following is a possible representation of the solution:

${\displaystyle u(r,\varphi ,t)=\sum _{\nu =-\infty }^{\infty }\sum _{n=0}^{\infty }\left({\underline {A}}_{\nu ,n}\cdot J_{\nu }(k_{n}\cdot r)\cdot \operatorname {e} ^{\operatorname {j} (\omega _{n}t-\nu \varphi )}\right)\quad {\text{mit}}\quad k_{n}={\frac {\omega _{n}}{c}}\quad {\text{und}}\quad J_{\nu }\left({\frac {\omega _{n}}{c}}\cdot a\right){\stackrel {!}{=}}0}$

Here, the zero point problem is the condition that a waveform with the angular frequency is a possible solution. We are looking for the zeros of the Bessel function used. ${\displaystyle \omega _{n}}$

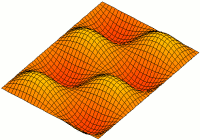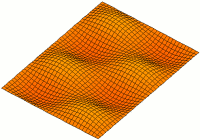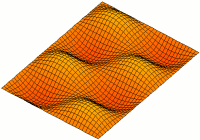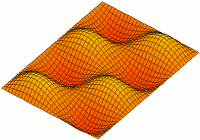
Oscillation of the undamped rectangular membrane

Two-dimensional standing wave in a rectangular frame with the largest possible wavelength

When describing an undamped rectangular membrane, the d'Alembert oscillation equation is used in Cartesian coordinates . The homogeneous Dirichlet boundary condition also applies here as boundary condition . So the differential equation looks like this:

${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}=0\quad {\text{mit}}\quad u(a,y,t)=u(x,b,t)=u(0,y,t)=u(x,0,t)=0}$

In this case the solution consists exclusively of trigonometric functions, which can be represented as a series as follows :

${\displaystyle u(x,y,t)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }\left(A_{n,m}\cdot \sin \left(k_{n}x\right)\cdot \sin(k_{m}y)\cdot \cos(\omega _{nm}t-\phi )\right)\quad {\text{mit}}\quad k_{n}={\frac {\pi n}{a}}\quad k_{m}={\frac {\pi m}{b}}\quad \omega _{nm}=c\cdot {\sqrt {k_{n}^{2}+k_{m}^{2}}}}$

The sub-functions for different n, m are called modes or natural oscillations . By defining the respective amplitude values, all possible waveforms can be represented. B. are not sinusoidal. ${\displaystyle A_{n,m}}$