This article or the following section is not adequately provided with
supporting documents (
e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and
including good evidence.
Zeros of functions are arguments ("x-values") which, when used, return the function value ("y-value") zero. The word component "position" indicates that these are elements of the domain of definition . In real functions exactly the points are the axis on which the graph of a function , the affected axis or cuts. Polynomial zeros are also called roots .



Zeroing real-valued functions
definition
Verbal definition
An element of the definition set of a function is called the zero of if holds. One then also says: has a zero at , or disappears at that point








example

The values 3 and −3 are zeros of the function , because
and
.




The value 0 is not a zero, because
.


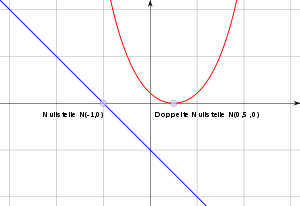
Multiple zeros
Definitions

Polynomial with zeros of order 1, 2 and 3
If a polynomial function is or at least continuous and differentiable at the zero , the zero can be “split out”. More precisely: there is a continuous function so that for everyone .







There are then two cases:
-
 . In this case it is called a simple zero .
. In this case it is called a simple zero .
-
 , ie also has in a zero. In other words, even after the root of it has been divided, is still a zero. In this case one calls a multiple zero of .
, ie also has in a zero. In other words, even after the root of it has been divided, is still a zero. In this case one calls a multiple zero of .






To determine whether it is a single or a multiple zero, one uses the fact that the value is equal to the derivative of at that point . The following criterion is obtained for a differentiable function :





- A zero of is a multiple zero if and only if is.



If it is more often differentiable, then this process can be repeated. One defines:

Let it be a natural number . A (at least) times differentiable function on an open subset has a (minimum) - multiple zero or a zero of order (at least) when itself and the first derivatives of at the site assume the value zero:












Be now at least once differentiable. Is a -fold zero, but not a -fold, so






this is what the order or multiplicity of the zero is called.

example

with the derivatives
-
 .
.
It is true that there is a zero of . Further applies



-
 but .
but .
Thus 1 is a triple, but not a quadruple zero of , i.e. a zero of the multiplicity 3.

Other properties
- A function has a -fold zero at if and only if has a zero and a -fold zero at .







- A -time continuously differentiable function has an at least -fold zero at if and only if there is a continuous function such that





-
 and
and 
- applies.
- A -time continuously differentiable function has a zero of the multiplicity if and only if there is a continuous function such that





-
 and
and 
- applies.

has a zero of the order infinite at 0, see also analytical function .
Existence and calculation of zeros
The existence of a zero can often be deduced indirectly from the intermediate value theorem: If of two function values , a continuous function, one is positive and one is negative, then there is at least one zero between and . (To put it clearly, the function graph that connects the two points and must intersect the -axis.)








Depending on the function, it can be difficult or impossible to explicitly determine the zeros, i.e. the equation

after dissolving. In this case, approximate values for zeros can be calculated using various numerical methods , for example bisection (interval halving method ), Regula falsi or a suitable fixed point iteration for continuous functions, the Newton method or Halley method for differentiable functions, the Weierstraß (Durand-Kerner) -Verfahrens or Bairstow method for polynomials determined.

In the list of numerical methods you can find the zero point search under the chapter Nonlinear Systems of Equations.
Zeroing of polynomial functions
If a ring and a polynomial are over , then an element is called the zero of , if the substitution of in zero results in:

![p \ in R [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec996b40aaba66391622fa52b5bfa7e65f2914e)






If a ring homomorphism, then zeros of in can be defined analogously .



With the help of the polynomial division one can show that there is a zero of if and only if is divisible by , ie if there is a polynomial such that






applies. This statement is sometimes called the zero set ; However, there is a risk of confusion with Hilbert's zero set .
A - multiple zero or zero of the order is an element , so that is divisible by . One also calls the multiplicity or multiplicity of the zero.






Determination of the zeros of small degree polynomials
For polynomials over a body whose degree is at most four, there are general solution formulas with radicals to determine the zeros directly:
Polynomials with integer coefficients
If a polynomial with integer coefficients, then every integer zero is a factor of .


From Gauss's lemma it follows: If a normalized polynomial with integer coefficients, then every rational zero is an integer and thus a divisor of .


Example:
The divisors of the absolute term of are not zeros, so they have no rational zeros. Since every factorization of would have to contain a linear factor, it follows that over is irreducible .






Polynomials with real coefficients
Polynomials of odd degree over the real numbers always have at least one real zero; this follows from the interim value theorem . Another reason (provided the fundamental theorem of algebra is already available) is the following: Genuinely complex zeros of real polynomials always appear as pairs of complex conjugate numbers. Polynomials of even or odd degrees always have an even or odd number of real zeros if you count every zero according to its multiplicity. One application of the latter principle is the numerical Bairstow method .
Example:
The polynomial has the zero , which can easily be guessed as a divisor of the absolute term. This gives by polynomial division


from which the two complex conjugate zeros and result.


Polynomials with only real zeros
If a polynomial whose zeros are all real, then these lie in the interval with the end points


Example:
The polynomial has the four real zeros -3, -2, -1 and 1. Using the interval formula results

-
 .
.
The interval is rounded
- I = [-3.812; 1,312].
The zeros are therefore in the found interval.
For the formula changes into the well-known pq formula .

Polynomials with complex coefficients
The fundamental theorem of algebra says: Every non-constant polynomial over the complex numbers has at least one zero. By repeatedly splitting off linear factors to zeros, one obtains the statement that every polynomial

about the complex numbers in the form

lets write. Here are the different zeros of and their respective multiples.



Polynomials over fully evaluated bodies
Let it be a fully evaluated field with evaluation ring and remainder class field , and let it be a normalized polynomial. From Hensel's lemma it follows: If the reduction has a simple zero in , then it has a zero in .



![p \ in A [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/72f36d9d096bd6082804a67d3a6066bf3efd6c29)
![{\ bar p} \ in k [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2f2736c879aa5c45b2c871d0d9b5350c7f17d5)



Example:
Let it be the field of p -adic numbers for a prime number . Then is and . The polynomial breaks down into various linear factors, so it also has exactly zeros, ie contains -th roots of unity .




![X ^ {{p-1}} - 1 \ in {\ mathbb Z} _ {p} [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5dd0517edd6e3dcb9cc64029e1efc0d3d89b4a4)





Web links
 Wiktionary: Zero
Wiktionary: Zero - explanations of meanings, word origins, synonyms, translations
Individual evidence
-
^ Walz, Guido: Lexikon der Mathematik . Spektrum, Akad. Verl, Heidelberg, ISBN 3-8274-0433-9 ( Spektrum.de [accessed on March 19, 2020]).














































![p \ in R [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec996b40aaba66391622fa52b5bfa7e65f2914e)

































![p \ in A [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/72f36d9d096bd6082804a67d3a6066bf3efd6c29)
![{\ bar p} \ in k [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2f2736c879aa5c45b2c871d0d9b5350c7f17d5)



![X ^ {{p-1}} - 1 \ in {\ mathbb Z} _ {p} [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5dd0517edd6e3dcb9cc64029e1efc0d3d89b4a4)



