Regula falsi

The regula falsi procedure ( Latin regula falsi , rule of the wrong one ), also: Regula duarum falsarum positionum ( Latin regula duarum falsarum positionum , rule of the two-fold wrong approach ' ), falsy invoice rsp. Falsi calculation or linear input , is a method for the numerical calculation of zeros of real functions . It combines methods from the secant procedure and bisection .

The procedure (primitive form)

The first two iterations of the regula falsi method; The function f is shown in red , the secants in blue

Visualization of the Regula falsi as animation

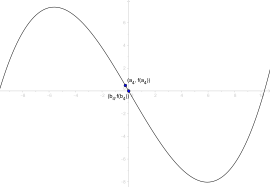
The Regula-falsi method starts with two digits (near zero) and whose function evaluations , various signs have. In the interval there is therefore a zero after the intermediate value theorem (for continuous ). Now you reduce the interval in several iteration steps and thus get an ever more precise approximation for the zero point. ${\displaystyle a_{0}}$ ${\displaystyle b_{0}}$ ${\displaystyle f(a_{0})}$ ${\displaystyle f(b_{0})}$ ${\displaystyle [a,b]}$ ${\displaystyle f}$

Iteration rule

In step one calculates: ${\displaystyle k}$

${\displaystyle \!\,c_{k}=a_{k-1}-{\frac {b_{k-1}-a_{k-1}}{f(b_{k-1})-f(a_{k-1})}}f(a_{k-1})}$  ${\displaystyle \!\,={\frac {a_{k-1}{f(b_{k-1})}-b_{k-1}{f(a_{k-1})}}{f(b_{k-1})-f(a_{k-1})}}}$.

If , the process is ended, because a zero is found with. Otherwise you select , as follows: ${\displaystyle f(c_{k})=0}$ ${\displaystyle c_{k}}$ ${\displaystyle a_{k}}$ ${\displaystyle b_{k}}$

• ${\displaystyle a_{k}=c_{k},\ b_{k}=b_{k-1}}$if and have the same sign and ${\displaystyle f(a_{k-1})}$ ${\displaystyle f(c_{k})}$
• ${\displaystyle a_{k}=a_{k-1},\ b_{k}=c_{k}}$if and have the same sign, ${\displaystyle f(b_{k-1})}$ ${\displaystyle f(c_{k})}$

and thus goes to the next iteration step.

Remarks

• The calculation of the corresponds to the application of the secant method with an iteration in the -th interval. In contrast to the secant method, there is always a zero in this interval. ${\displaystyle c_{k}}$ ${\displaystyle (k-1)}$
• Geometric can be interpreted as the zero of the secant and . ${\displaystyle c_{k}}$ ${\displaystyle \left(a_{k-1},f(a_{k-1})\right)}$ ${\displaystyle \left(b_{k-1},f(b_{k-1})\right)}$
• ${\displaystyle c_{k}}$is of course always in the interval . ${\displaystyle \left[a_{k-1},b_{k-1}\right]}$
• Convergence: As long as the -th interval is not strictly concave or convex, i.e. there is a change in sign of the second derivative in the interval , there is superlinear convergence . ${\displaystyle f}$ ${\displaystyle k}$

• Visualization of the Regula falsi
• 
• 
• 
• 
• 

Improvement of the procedure

If the interval is concave or convex, i.e. if the second derivative has the same sign everywhere in the interval, then one of the interval limits remains for all further iterations, because the secant is always below or above the function. The other interval limit now only converges linearly to the solution. ${\displaystyle f}$ ${\displaystyle [a_{k},b_{k}]}$

The following procedures can help.

Illinois, Pegasus, and Anderson / Björck procedures

Idea of ​​the procedure

The improved method is based on the following idea. If the "left" interval limit does not change in the current step - that means that the actual zero point lies between the "left" limit and the approximated zero point - one multiplies by a factor and brings the function value at the point closer to zero. ${\displaystyle x_{1}}$ ${\displaystyle f(x_{1})}$ ${\displaystyle 0<m<1}$ ${\displaystyle x_{1}}$

Either the distance of the approximation to the zero point is shortened in the next step or the zero point is approximated in the next step between the actual zero point and the "right" interval limit.

In the second case "right" and "left" are simply swapped for the next step. Since the second case always occurs at some point - even in convex intervals - it is certain that neither of the two interval limits will remain until the termination. Thus the convergence is guaranteed to be super linear.

algorithm

These methods have the following algorithm in common:

${\displaystyle \!\,{\begin{array}{l}{\mathsf {solange}}~\circledast (|x_{2}-x_{1}|\geq \varepsilon _{x},|f_{z}|\geq \varepsilon _{f}):\\~~\left[{\begin{array}{l}z:=x_{1}-{\frac {f_{1}}{s}}~\mathrm {mit} ~s={\frac {f_{2}-f_{1}}{x_{2}-x_{1}}}\\f_{z}:=f(z)\\{\mathsf {falls}}~f_{z}\cdot f_{2}<0:\\~~\left[x_{1}:=x_{2},~f_{1}:=f_{2},~x_{2}:=z,~f_{2}:=f_{z}\right.\\{\mathsf {falls}}~f_{z}\cdot f_{2}>0:\\~~\left[f_{1}:=m\cdot f_{1},~x_{2}:=z,~f_{2}:=f_{z},~x_{1}~{\text{bleibt}}\right.\\{\mathsf {sonst}}:\\~~\left[x_{1}:=z,~f_{1}:=f_{z},~x_{2}:=z,~f_{2}:=f_{z}\right.\\\end{array}}\right.\\~\\{\text{nimm }}z{\text{ als Näherung für }}x^{*}\end{array}}}$

Here, the interval boundaries in th step, and the function values at the points and . are the termination limits and the shortening factor. stands for an unspecified, two-digit Boolean function . Useful functions here would be the disjunction , the conjunction , the identity of the first and the identity of the second operand. In the first case, one of the two termination limits, in the second case both, in the third case only and in the fourth case must be fallen below, so that it becomes incorrect and the procedure is terminated. ${\displaystyle x_{1},x_{2}}$ ${\displaystyle k}$ ${\displaystyle f_{1},f_{2}}$ ${\displaystyle f_{z}}$ ${\displaystyle x_{1},x_{2}}$ ${\displaystyle z}$ ${\displaystyle \varepsilon _{x},\varepsilon _{f}}$ ${\displaystyle m}$ ${\displaystyle \circledast (\cdot ,\cdot )}$ ${\displaystyle \varepsilon _{x}}$ ${\displaystyle \varepsilon _{f}}$ ${\displaystyle \circledast (|x_{2}-x_{1}|\geq \varepsilon _{x},|f_{z}|\geq \varepsilon _{f})}$

The different procedures only differ in the reduction factor . ${\displaystyle m}$

Illinois proceedings

${\displaystyle m_{I}=0{,}5}$

Pegasus procedure

${\displaystyle m_{P}={\frac {f_{2}}{f_{2}+f_{z}}}}$

Anderson / Björck method

${\displaystyle m_{A/B}={\begin{cases}1-{\frac {f_{z}}{f_{2}}}&{\text{falls}}~1-{\frac {f_{z}}{f_{2}}}>0\\0{,}5&{\text{sonst}}\end{cases}}}$

Recursive implementation of the Pegasus method

The function to be examined and the termination criteria:

epsx, epsf seien definiert
f(x) sei definiert

The shortening factor for the Pegasus procedure:

m(f2, fz): return f2 ÷ (f2 + fz)

The actual, recursive algorithm:

betterFalsePosition(x1, x2, f1, f2):
  z := x1 − f1 · (x2 − x1) ÷ (f2 − f1) // Näherung für die Nullstelle berechnen
  fz := f(z)

  // Abbruchgrenze unterschritten?: z als Näherung zurückgeben
  if |x2 − x1| < epsx or |fz| < epsf then return z

  // ansonsten, Nullstelle in [f(xz), f(x2)]?: „Links und Rechts“ vertauschen, Nullstelle in [f(xz), f(x2)] suchen
  if fz · f2 < 0 then return betterFalsePosition(x2, z, f2, fz)

  // ansonsten: „verkürzen“ und Nullstelle in [x1, z] suchen
  return betterFalsePosition(x1, z, m(f2, fz) · f1, fz)

The method by which the procedure is started for the interval to be examined:

betterFalsePosition(x1, x2): return betterFalsePosition(x1, x2, f(x1), f(x2))

Remarks

• The convergence of the methods is super-linear and comparable to that of the secant method.
• Due to the superlinear, guaranteed convergence and the relatively low computational effort per iteration, these methods are usually preferable to other methods (such as Newton's method ) for one-dimensional problems .

history

The first manifestations of the Regula falsi can already be found in very old mathematical texts. For example, in the Rhind Papyrus (approx. 1550 BC), this method can be used to solve linear systems of equations .

The Indo-mathematical script “ Vaishali Ganit ” (approx. 3rd century BC) is among the oldest surviving documents that testify to the knowledge of the method of the double incorrect approach . The ancient Chinese mathematical text The Nine Chapters of the Mathematical Art (200 BC - 100 AD) also mentions the algorithm. In this text, however, the method was only applied to linear equations in examples , so that the solutions were achieved in just one iteration. Leonardo da Pisa (Fibonacci) described the procedure of the double wrong approach in his book “Liber Abaci” (1202 AD), based on a method he had learned from Arabic sources.

Even Adam Ries knew the regula falsi and described the method as follows:

“Is added with two wrong numbers, which should be checked thoroughly according to the task to the extent required by the number sought. If they lead to a higher result than is actually correct, denote it with the sign + plus, but if the result is too small, describe it with the sign -, called minus. Then subtract one shortfall from the other. What remains as the rest, keep for your divider. Then cross-multiply one wrong number by the shortfall of the other. Subtract one from the other, and what remains as the remainder, divide by the previously calculated divisor. So the solution to the problem comes out. But if one wrong number leads to a result that is too large and the other to a result that is too small, add the two shortfalls. What comes out of this is your divider. Then multiply crosswise, add and divide. This is how the solution to the task comes out. "

Web links

Commons : Regula falsi  - collection of images, videos and audio files

Individual evidence

1. ↑ ^{a b} Leonardo da Pisa : Liber abbaci . 1202, chapter 13. De regula elcataym qualiter per ipsam fere omnes erratice questiones soluantur.
2. ↑ ^{a b} Adam Ries : Calculation on the lines and springs . 1522 (see Matroids Matheplanet: Die regula falsi - Adam Ries' most important arithmetic rule ).
3. ^ Arnold Buffum Chase: "The Rhind Mathematical Papyrus", Free Translation and Commentary with Selected Photographs Transcriptions, Transliterations and Literal Translations by Arnold Buffum Chase, Editors: Phillip S. Jones, Bruce E. Meserve, The National Council of Teachers of Mathematics, Classics in Mathematics Education A Series, 1979