Disjunction
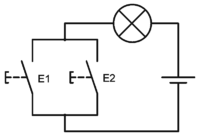
When button E1 or E2 is pressed, the lamp lights up.
This logical or also includes the case that both are pressed at the same time.
Disjunction (“Or-connection”, from Latin disiungere “separate, distinguish, not mix”) and adjunction (from Latin adiungere , “add, connect”) are the names in logic for two types of statements , each of which two declarative sentences by an exclusive or , or by a non-exclusive or are connected:
- The non-exclusive disjunction ( alternative , adjunction , inclusive or , OR ) “A or B (or both)” says that at least one of the two statements involved is true . So it is only wrong if both A and B are wrong.
- The exclusive disjunction ( contravalence , exclusive or , XOR ) "(either) A or B (but not both)" says that exactly one of the two statements involved is true (if the disjunction is true). The exclusive disjunction is therefore false if either both statements involved are false or if both statements involved are true. The exclusive disjunction is also called contravalence and is dealt with in more detail under this keyword.
- Only occasionally is the non-exclusive disjunction of the negations of the statements involved referred to as the disjunction of A and B, that is, the statement "not A or not B (or both)" or equivalently "not (A and B)". This connection is u. a. Sheffer's line , NAND or exclusion (in the sense of logic) called. It corresponds to the set-theoretic term disjoint .
Seldom used terms for the disjunction are alternative , contrajunction , bisubtraction and alternation . The ambiguous use of “disjunction” etc. can be traced back to the different roles of natural language or language . The partial statements of a disjunction (adjunct) are called disjuncts (adjuncts), the word linking the partial statements ("or") is called disjunctor ( adjunct ).
Non-exclusive disjunction
The non-exclusive disjunction (alternative, adjunction) is a compound statement of the type “A or B (or both)”; it says that at least one of the two statements involved is true.
- Notation
In Polish notation , the capital letter A is used for disjunction :
- Aab
In the notation of a link between statements, the symbol ( Unicode : U + 2228, ∨) stands for the non-exclusive disjunction as a propositional join . It is similar to the symbol for the union and is reminiscent of the letter “v”, with which the Latin word “vel” begins, which stands for such a non-exclusive or.
The truth table for the vel function ( OR function of a gate ) as a truth value function of the non-exclusive disjunction is thus:
| true | true | true |
| true | not correct | true |
| not correct | true | true |
| not correct | not correct | not correct |
A disjunction is a Boolean expression , it is associative and commutative .
From what has been said follows:
- If A is false and B is false, the disjunction is false; in any other case it is true.
- If the disjunction is false, then both A and B are false.
- If the disjunction is true, one of the following must exist:
- both disjoints are true
- A is false and B is true or
- A is true and B is false
example
The statement "Tom helps paint or Anna helps paint" consists of the following parts:
- the partial statement / the disjoint A: "Tom helps with deleting"
- the disjunctor “or” is not understood here as being exclusive
- the partial statement / the disjoint B: "Anna helps with painting"
Neither of the two partial statements excludes the other here. The statement is false if neither Tom nor Anna help with painting, otherwise true. It is especially true when both Tom and Anna help with the painting.
Exclusive disjunction
The exclusive disjunction (contravalence, XOR) is a compound statement in which two statements are linked with the phrase “either - or (but not both)”, for example the statement “Anna either studies French or she studies Spanish (but not both) ). ”This excludes the case that both partial statements are true - in the example, the case that Anna studies both French and Spanish - this is where the difference to the non-exclusive disjunction lies. The Latin expression for the exclusive or is "aut - aut".
The truth table for the aut function ( XOR function of a gate ) as a truth value function of the exclusive disjunction is thus:
| true | true | not correct |
| true | not correct | true |
| not correct | true | true |
| not correct | not correct | not correct |
Derivations in the calculus of natural inference
From a statement A disjunction can A or B are closed.
For the statement B added by the disjunction to the already given statement A , no previous prerequisites have to be met, as the following example deduction shows.
| row | statement | rule |
|---|---|---|
| 1 | premise | |
| 2 | 1 (introduction of disjunction) |
To resolve a disjunction, the same statement must be derived from both parts of the disjunction.
| row | statement | rule |
|---|---|---|
| 1 | premise | |
| 2 | adoption | |
| 3 | (And elimination) | |
| 4th | 2,3 (implication insertion) | |
| 5 | adoption | |
| 6th | 5 (and elimination) | |
| 7th | 5.6 (implication insertion) | |
| 8th | 1,4,7 (disjunction elimination) |
(The symbol ∧ in the table denotes the conjunction .)
See also
Web links
- Ray Jennings: Disjunction. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
Individual evidence
- ↑ Kuno Lorenz : "Disjunction", in: Jürgen Mittelstraß (Ed.): Encyclopedia Philosophy and Philosophy of Science. Volume 1. Stuttgart: Metzler 1995, ISBN 3-476-02012-6 , p. 491
- ↑ cf. Principia Mathematica 1.3
- ↑ Esther Ramharter, Georg Riekh: The Principia Mathematica in a nutshell. ÖBV hpt, Vienna 2006, p. 20
- ^ A b Niko Strobach : Introduction to logic. WBG Darmstadt, Darmstadt 2011, 2nd edition, p. 58