Logic gate
| Gate types | |
|---|---|
| NOT | |
| AND | NAND |
| OR | NOR |
| XOR | XNOR |
A logic gate , only gate , ( Engl. (Logic) gate ) is an assembly (nowadays virtually always an electronic circuit ) for implementing a Boolean function , the binary input signals are processed to produce a binary output signal. The input signals are generated through the implementation of logical operators such as conjunction ( AND gate ), disjunction ( OR gate ), contravalence ( exclusive or gate ) or negation ( non-gate) is converted into a single logical result and mapped onto the output signal . In addition to the gate functions mentioned, the equivalents with a negated output should also be mentioned: NAND gate (not-and), NOR-gate (not-or), XNOR-gate (non-exclusive-or); German names of the latter gates are unusual.
In principle, all logical links can be implemented as gates. Several logic gates can be interconnected to form a flip-flop , latch or multiplexer , data memories and counters can be created from several flip-flops , and a microprocessor can be assembled from several of these circuits . Individual logic gates are offered as an integrated circuit (IC); in more complex circuits they sometimes occur tens of millions of times within an IC. However, they can also be constructed from discrete electronic components , using switches or relays, or even represented using fluidic components. There are also mechanical structures in historical calculating machines.
The so-called switching algebra is used to implement and simplify a complex logical function .
The number of gate equivalents is used as a measure of the logical complexity of a circuit.
technology
There are different options for the technical implementation despite the same operation. Nowadays, circuits for logic gates consist entirely of transistors , with a few exceptions . The signal represents the logical states through two voltage values, which are commonly referred to as “0” or “1”, “low” or “high” (“L” or “H” for short); the former also allow an interpretation as binary digits . Limits are defined for the voltage value within which the transistors - which are subject to production tolerances - either switch safely to conducting or safely to blocking. The output signal representing the result of the operation can in turn be connected to the inputs of other gates; this allows more complex, versatile circuits to be created.
Electronic gates are available as TTL , CMOS or BiCMOS components in the form of individual integrated circuits for a few cents. They are basically based on the two transistor families of the bipolar transistors (TTL) and the field effect transistors , more precisely the MOSFETs (CMOS), as well as on the combination of both families (BiCMOS). They form the core of microprocessors , or thousands of them can be programmed using software in FPGA or PLD ICs. The NAND and NOR gates are of particular importance here, since all binary functions according to Quine / McCluskey can be traced back to the three basic elements AND, OR and NOT. Again, OR and NOT can be represented using NAND gates, or AND and NOT using NOR gates. You can therefore implement any logic circuit using NAND or NOR components alone if you can accept the gate throughput times and the signal edge times.
history
The binary system was first described mathematically exactly by Gottfried Wilhelm Leibniz (published in 1705), whereby Leibniz also explained how the principles of arithmetic and logic can be combined using this system.
The first logic gates were realized mechanically. In 1837, the English inventor Charles Babbage designed the Analytical Engine, a calculating machine that is now an important step in the history of the computer . His "logic gates" worked on the basis of mechanical reactions, while electromagnetic relays were used later.
In 1891, the American Almon Strowger applied for a patent for a "unit that contains a logic gate switch circuit", but this did not establish itself until the 1920s. In 1898, the inventor Nikola Tesla began archiving and refining such units and enforced the use of electron tubes instead of relays. Lee De Forest finally changed the circuit concept of the Fleming electron tube in 1907 so that it could be used as an AND gate.
The Austrian philosopher Ludwig Wittgenstein introduced the first truth table in Theorem 5.101 of his treatise Tractatus Logico-Philosophicus in 1921 , but without naming it that way. Walther Bothe , the inventor of the coincidence circuit , received the Nobel Prize (1954) in part for the first modern electronic AND gate from 1924. Konrad Zuse designed and built electromechanical logic gates for his computer Z1 (from 1935 to 1938).
The American mathematician Claude Elwood Shannon founded Wittgenstein's ideas in 1937 with the introduction of Boolean algebra in the evaluation and design of electrical circuits.
Helmut Schreyer , who had obtained his doctorate in circuit technology in 1941, built an electronic computer system with 100 tubes on a trial basis in 1942 and an electronic translator from decimal to binary numbers in 1944.
The first integrated logic gate goes back to Jack Kilby in 1958 and comprised around ten components. Ten years later made Texas Instruments circuits in transistor-transistor logic (TTL circuits series 74xx ) in large series. They quickly became the basis of industrial automation.
Current research projects deal with molecular logic gates.
Truth table
The possible output states of a logic gate can be displayed in a truth table depending on the input states. It lists all possible combinations of the input signals and provides the associated output signals. From this one can read out logical formulas relatively easily. With the disjunctive normal form (1 as result), the individual lines with the same output values are linked with logical or and the individual inputs with logical and . The reverse is true for the conjunctive normal form (0 as the result). A KV diagram (see below) can be used to obtain a compact formula.
KV diagram
The Karnaugh-Veitch diagram is a simple way of building a logical formula that is as compact as possible from the disjunctive or conjunctive normal form. This compact form is created through the sensible combination of zeros or ones and “favorable” interpretation of the redundant fields (“empty” fields that have no influence on the function).
Types of logic gates and symbolism
Logic gates are designated with circuit symbols that are defined according to different, more or less parallel standards.
| Surname | function | Symbol in circuit diagram | Truth table |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
IEC 60617-12: 1997 & ANSI / IEEE Std 91 / 91a-1991 |
ANSI / IEEE Std 91 / 91a-1991 | DIN 40700 (before 1976) | ||||||||||||||||||
|
AND gate (AND) |
|

|
|

|
|
|||||||||||||||
|
OR gate (OR) |
|

|
|

|
|
|||||||||||||||
|
Not gate (NOT) |
|

|
|

|
|
|||||||||||||||
|
NAND gate (NOT AND) (NOT AND) |
|

|
|

|
|
|||||||||||||||
|
NOR gate (NOT OR ) |
|

|
|

|
|
|||||||||||||||
|
XOR gate (exclusive OR, non-equivalence) (EXCLUSIVE OR) |
|

|
|
 or 
|
|
|||||||||||||||
|
XNOR gate (Exclusive- NOT -OR, equivalence) (EXCLUSIVE NOT OR) |
|
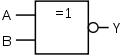
|
|
 or 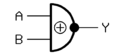
|
|
|||||||||||||||
The German symbols (right column) used to be common on the European continent; In the English-speaking world, the American symbols (middle column) were and are common. The IEC symbols have met with limited acceptance internationally and are (almost) completely ignored in American literature.
See also
literature
- Ulrich Tietze, Christoph Schenk: Semiconductor circuit technology . 12th edition. Springer, 2002, ISBN 3-540-42849-6 .
Web links
Individual evidence
- ↑ Helmut Schreyer. Retrieved January 16, 2020 . , Institute for Telecommunication Systems, Technical University Berlin .






















