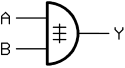
Exclusive-or gate
| Gate types | |
|---|---|
| NOT | |
| AND | NAND |
| OR | NOR |
| XOR | XNOR |
An exclusive-or-gate , also XOR-gate (from English e X clusive OR ' exclusive or ' , "either or") is a gate with two inputs and one output, where the output is logical "1" when on only one input is “1” and the other “0”. The exclusive-or link is also referred to as anti- or contravalence .
This means that the inputs have to be wired differently in order to get a "1" at the output. "1" must be present either at one or the other input. In contrast to a simple OR link, the condition is considered not fulfilled if a "1" is present at both inputs. In the case of an exclusive or, the result is a "0" in this case.
symbolism
In the literature, the exclusive or is marked with different symbols. It is common to spell out the operator as “XOR” or “EOR”, e.g. B. with the expression " A XOR B ". When using the symbol "+" for the logical or , the symbol " " is used for the exclusive or. When using “∨” for the logical or, however, “⊻” is used for the exclusive or. The character is used as a bitwise operator in C (and programming languages derived from it) .
^
| function | Circuit symbol | Truth table | Relay logic | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IEC 60617-12 | US ANSI 91-1984 | DIN 40700 (before 1976) | ||||||||||||||||||
|
|
or 
|
|
||||||||||||||||||
The equals sign = makes it clear with the circuit symbol currently valid in Germany that the output is only "1" if there is a "1" at the inputs (high level, logical "1").
synthesis
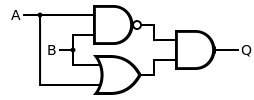
| Structure of an exclusive-OR gate from four NAND gates |
Structure of an exclusive-or gate from AND, OR and NOT gates (the latter for the negation of one of the AND gate inputs) |
Structure of an exclusive-or gate from AND, OR and NAND gates |
The figure on the left shows the structure of an exclusive-OR gate from four NAND modules according to the logical non-equivalence
The figure in the middle shows the structure of an exclusive-or-gate from not- , and- and or-blocks . Due to the large number of different components, however, it is only relevant for implementation in hardware in exceptional cases:
The illustration on the right shows the structure of an exclusive-or gate from a NAND , an AND and an OR gate .
programming
The exclusive-or link can also be calculated by adding two bits modulo 2. To do this, calculate the simple sum of the input signals, divide the sum by 2 and then consider the remainder of the division. If the sum is an even number, the remainder is equal to zero, if it is odd, the remainder is equal to one. Furthermore, the simple exclusive-OR link between two input signals can also be viewed as an indication of the inequality of the input bits. This also applies to any even number of input signals.
application
Addition of binary numbers
An exclusive-or gate can be used to add binary numbers. In addition, a so-called carry is formed here, for example with the help of an AND gate, when the state x = 1 and y = 1 . This carry must be taken into account when adding the next higher bit as "1". The adder of the Von Neumann adder uses this logic.
Cryptography
The one-time-pad encryption process that has been proven to be secure is usually implemented with the aid of an exclusive-or link. The message to be encrypted ( plain text ) is first encoded as a bit sequence. A second random bit sequence that is the same length as the message is used as the key . The ciphertext is created by exclusively-or-associating the first bit of the message with the first bit of the key, the second bit with the second and so on. If you then carry out the same exclusive-or link with the ciphertext and the key, you will get the original message again.
safety
- If an attacker gets the clear text and the ciphertext, he can very easily find out the key by means of an exclusive-or link and try it out with other ciphertexts. It is hardly possible to obtain the key with other methods (e.g. AES ). However, this does not play a role in the one-time-pad procedure, since completely independent keys are used for each message.
- Attack on exclusive-or-encrypted data if the key length is shorter than the ciphertext:
- With exclusive-OR operations of the cipher text is with ciphertext n processes, wherein ciphertext n corresponds to n bits to the right-shifted ciphertext. How many bits remain the same after the exclusive-or operation? The key length corresponds to the shift n at which the result of ciphertext XOR ciphertext n most closely resembles the ciphertext.
- The key length n has now been found. The operation ciphertext XOR ciphertext n gives the same result as plaintext XOR plaintext n . Because it applies:
-
There is usually enough plain text to completely decipher the message. Because it applies:
- Decryption is much easier if the key is n bits long and the same bits are repeated m times in plain text , where m represents a multiple of n . Here as an example a repetition of zeros; the key is
1010. Since the sequence is1010repeated in the encrypted text , the attacker can assume that the plaintext at this point consisted of zeros and was the key1010(or the ciphertext made of ones and the key was0101):
Plain text XOR key → ciphertext 11111001 000000000000 XOR 10101010101010101010 → 01010011 101010101010
Exclusive-or encryption can, however, be significantly improved by generating a sufficiently long key from a short password. One example of this is encryption using RC4 , which is now considered unsafe. Encryption with Spritz is more secure, but a little slower .
Checksum generation
0101 XOR 1011 = 1110
1011 XOR 1110 = 0101
0101 XOR 1110 = 1011
The parity is formed from two bit sequences, assumed 0101and 1011, using the exclusive-or link : (first line in the example on the right). This parity must be transmitted or saved together with the two bit sequences. If the first bit sequence ( ) is now lost, it can be restored in that the second bit sequence ( ) is exclusively-or-linked with the parity (second line). The second bit sequence could be restored analogously (third line).
111001011011
Frequency doubling
A very simple frequency doubling of square waves in the frequency range up to a few 100 MHz can be achieved with an exclusive-OR gate if one input is immediate and the other with a slightly delayed signal (shown in the drawing by an RC element, but is conceivable also circuits, for example with gate delay times , such as two inverters) is fed. The exclusive-or gate switches on a rising and falling edge; the resulting needle pulses are phase-bound and about as short as the signal delay used. Since this method does not use a resonance filter, the input signal can have almost any pulse duty factor or be heavily frequency-modulated , but in general a pulse duty factor of 50% cannot be achieved.
Switchable inverter
A signal is present at one input, the other serves as a control input. If the control input is at logic "0", the signal is allowed through without change. If the control input is at logic "1", the gate behaves like an inverter.
CMOS implementation
The implementation shown above using AND and OR gates requires 16 transistors in CMOS technology. A direct implementation (right) only requires 12 transistors and with tricks, with a loss of speed, six transistors or four transistors. To understand: T1 + T2 and T3 + T4 invert the input signals. With high potential at both inputs (A + B), T7 + T8 conduct and pull output Y to low potential. If both inputs are at low potential, T11 + T12 conduct, as there is an inverter in front of both that reverses the input signal.
There are also implementations that provide both XOR and NXOR as a result.
A full adder optimized in this way only requires 26 transistors (2 × 4 transistors for the exclusive or the sum, 3 × 4 transistors for the 2-way NAND and 1 × 6 transistors for the 3-way NAND for the carry ). A 64 × 64-bit multiplier can be implemented as a switching network with almost 140,000 transistors.
literature
- Ulrich Tietze, Christoph Schenk: Semiconductor circuit technology . 12th edition. Springer, 2002, ISBN 3-540-42849-6 .
- Klaus Beuth: Digital technology . 10th edition. Vogel, 1998, ISBN 3-8023-1755-6 .
- Manfred Seifart, Helmut Beikirch: Digital circuits . 5th edition. Technology, 1998, ISBN 3-341-01198-6 .
Individual evidence
- ↑ Bruce Schneier: Applied Cryptography. 2006.
- ^ A b Jürgen Schmidt: KRACK - this is how the attack on WPA2 works. In: heise Security. Heise Medien GmbH & Co. KG, October 19, 2017, accessed on October 24, 2017 .