Bitwise operator
In computer science , a bitwise operator is an operator that is applied to one or two bit sequences or binary numbers at the level of individual bits . On many computers, bitwise operations are slightly faster than addition and subtraction operations and significantly faster than multiplication and division operations.
Bitwise operators
NOT
A bitwise NOT or complement is a one- digit combination that performs a logical negation of each bit and thus forms the one's complement of a binary number. Each 0is 1exchanged for one and vice versa. Example:
NICHT 0111
= 1000
In many programming languages of the C family, this is NOT represented bit by bit as ~( tilde ). In contrast to this, with the logical operator ! (exclamation mark) for logical NOT the entire value is interpreted as a Boolean expression trueor false. The logical NOT is not a bitwise operation.
NICHT (Logisch): !1d = 0d; !5d = 0d NICHT (Bitweise): ~1d = 0d; ~5d = ~0101b = 1010b = 10d
OR
A bitwise OR is applied to two bit sequences of the same length and returns a bit sequence of the same length by combining bits in the same place (the first bit, the second bit, etc.) with a logical OR (logical disjunction ). For each pair, the result 1bit 1is if the bit of the first bit sequence is OR the bit of the second bit sequence 1, otherwise the result bit is 0. Example:
0101 ODER 0011 = 0111
In the programming languages related to C, the bitwise OR is represented by |( vertical line ). The Boolean counterpart to this, the logical OR , which interprets its operands as Boolean values, is shown as ||(two vertical lines).
The bitwise OR is used when multiple bits are used as flags ; the bits of a single binary number can each represent their own Boolean variable. If you apply the bitwise OR to such a binary value and a "mask" that 1contains one at certain points , you get a new bit sequence in which these bits are set in addition to the originally available ones. Example:
0010
can be viewed as a list of four flags. The first, second and fourth flags are not set ( 0), the third flag is set ( 1). The first flag can be set by linking this bit sequence with a bit sequence that only has one in the first position 1:
0010 ODER 1000 = 1010
This technique is used to save memory space when programs have to manage a large number of Boolean values.
XOR
A bitwise exclusive OR is applied to two bit strings of the same length and performs the logical XOR operation on each pair of corresponding bits. The result 1bit is if the two bits are different and 0if they are the same. Example:
0101 XOR 0011 = 0110
In the programming languages related to C, the bitwise XOR is represented as ^( circumflex ).
In assembly language , bitwise XOR is sometimes used to set the value of a processor register to 0. If you apply XOR to two identical operands, you always get 0. In many architectures, this operation requires less computing time than is required for loading 0and storing in the register.
The bitwise XOR can also be used to switch flags in bit sequences. Example:
0010
The first and third bits can be switched simultaneously by XORing this bit sequence with a mask that has set bits 1 and 3:
0010 XOR 1010 = 1000
This technique can be used to manipulate bit strings that represent multiple Boolean variables.
AND
A bit-wise AND is applied to two bit sequences of the same length and performs the logical AND operation ( logical conjunction ) on every pair of corresponding bits. The result 1bit is if both bits 1are, otherwise 0. Example:
0101 UND 0011 = 0001
In the related C programming the bitwise AND is by &( ampersand , Eng. Ampersand ), respectively. The Boolean counterpart to this, the logical AND , interprets its operands as Boolean values and is represented as &&(two ampersand).
The bitwise AND can be used to mask a bit sequence . This allows parts of a bit string to be isolated and to determine whether a particular bit is set or not. Example:
0011
To find out whether the third bit is set or not, a bitwise AND is applied to it with a mask that 1contains one in the third position :
0011 UND 0010 = 0010
Since the result is not zero, the third bit in the original bit sequence must 1have been one. This application of bitwise AND is called bitwise masking because parts that should not be changed or are not important for the calculation are masked out.
The bitwise AND can be combined with the bitwise NOT to clear bits. For example, in the bit sequence
0110
the third bit from the right can be cleared (i.e. 0set to) so that the result 0010comes out.
This is done by applying an inverted mask (the zero must be set in the place of the digit to be changed) on our bit sequence. We can invert with the NOT operator.
NICHT 0100
= 1011
Then the bit sequence and the mask are linked using the AND operator:
0110
UND 1011
= 0010
With the bitwise AND it is also possible to calculate an n -bit number modulo 2 k by ANDing it with 2 k -1. This sets all bits from the k plus first bit to 0, which then corresponds exactly to the result of the modulo calculation.
Example: 17 corresponds to mod 8 = 1
10001 (17)
UND 00111 (7 = 8-1)
= 00001
Bitwise shifts
In the bitwise shifts (engl. Bitwise shift ) the bits as a single character at a specific be construed bit position - and not as pairs of corresponding bits as in the above operations. Here, the joint of the bits in the means arithmetic shift a binary number or in the - more elementary bit - logical shift a bit string (. Resp an unsigned (engl. Unsigned ) binary number). The main difference lies in the treatment of the possible sign bit. In terms of circuitry, bit-by-bit shifts and rotations by any number of digits can be implemented in the form of barrel shifters .
In these operations, the binary characters are shifted to the left or right by a specified number of bit positions . The directional information is always understood in the (big-endian) standard convention of the dual system , regardless of the computer architecture (and its endianness ) : left means multiplication and right means division with a power of two. Registers of the processors and data types of the programming accommodate a defined finite number of bits, which is why the specified number of bits at one end from the register or data "pushed", while the same number at the other end "pushed" ( "pulled in") is.
In this way, the bit-wise shift operations induce addressing of the bits within a byte.
- example
Symbolism:
- "<<" (in some languages "shl") Shift to the left by the value given after it
- ">>" (in some languages "shr") Shift to the right by the value given after it
In languages like C, shifts to the right are padded with zeros (unsigned or non-negative) or ones (signed and less than zero), depending on the data type and, if applicable, the sign . Other programming languages (such as Java) use their own operator instead >>>, which is always padded with zeros:
00111100 << 1 = 01111000 00111100 << 2 = 11110000 (signed erzeugt einen arithmetischen Überlauf) 11111100 << 2 = 11110000 (signed ohne arithmetischen Überlauf) 01001111 >> 1 = 00100111 11110000 >> 2 = 11111100 (signed) 11110000 >> 2 = 00111100 (unsigned) 11110000 >>> 2 = 00111100 (signed und unsigned) 01001111 >>> 1 = 00100111 (signed und unsigned)
A logical (or arithmetic) shift by (bit positions) to the left is equivalent to a multiplication by , provided that no 1 bits are shifted out (or into the sign position). An arithmetic shift by (bit positions) to the right is equivalent to a division by ; 1 bits that are shifted out are lost.
00001100 << 2 = 00110000
This method is an alternative to multiplication or division by powers of two. Division results are cut off. It is also possible to calculate an n -bit number modulo 2 k by shifting it by n – k to the left and then to the right again. The modulo calculation can be carried out a little faster using the bitwise AND with 2 k -1.
A shift by 0 bit positions does not change the value ("identical mapping"). If the shift by bit positions is defined, then the following applies to both (both) logical and (both times) arithmetic shifts:
((xyz) >> m) >> n = (xyz) >> (m+n) (signed und unsigned) ((xyz) << m) << n = (xyz) << (m+n) (signed und unsigned)
In other words: Apart from the restriction on the maximum number of shift positions, from which the behavior (implementation-dependent and) can be undefined, it is sufficient to define the behavior of the shift operations for a (single) shift position.
Logical shift
In a logical shift (engl. Logic shift ), the bit shifted out are discarded and zeroes tightened, irrespective of the sliding direction and sign. Therefore, logical and arithmetic shifts to the left (except for the possible setting of flags) are identical operations. However, the logical right shift inserts zeros instead of copies of the sign bit. Therefore, the logical shift is used for bit strings or unsigned binary numbers, while arithmetic shifts are used for signed two's complement numbers.
Arithmetic shift
In contrast to the logical shift in has arithmetic (sometimes called algebraic ) displacement (engl. Arithmetic shift ) the role of the most significant bit of the sign (as shown as a two's complement ). The underlying data type is the signed ( signed) binary integer for which the compiler generates the arithmetic shift. Bits pushed out are lost. With a shift to the right, copies of the sign bit are inserted at the sign position ( sign propagation ); with a shift to the left, zeros are traced on the right side. Example (4-bit register):
1100 RECHTS-SHIFT um 1 = 1110
0110 LINKS-SHIFT um 1 = 1100
When shifting to the right, the least significant bit ( the one that is furthest “right” in conventional binary representation, the one) bit is shifted out and the most significant bit (MSB), the “sign bit”, is reinserted at the high value (“left”) end the sign of the number is retained. When shifting to the left, a new one is 0inserted at the lower ("right") end and the most significant bit is shifted out of the register. If the new sign bit is different from the one that was last postponed (that is, the sign changes during the last shift process), the overflow or carry flag is set in many computer families , otherwise it is deleted.
An arithmetic shift by (bit positions) to the left is equivalent to a multiplication by (provided that no overflow occurs). An arithmetic shift of a signed ( ) binary number ( two's complement number ) to the right corresponds to an integer division by with rounding to the next lower number - examples: and .
signed1>>1 == 1>>31 == 0(-1)>>1 == (-1)>>31 == -1
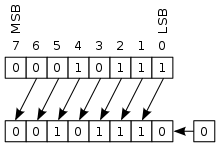
Cyclical shift
Cyclical shift without carry bit
Another form of the bitwise shift is the cyclic shift (engl. Circular shift ) or bitwise rotation . In this operation, the bits “rotate” as if the left and right ends were connected. The bit that is shifted in has the same value as the bit that is shifted out of the register. This operation preserves all existing bits and is used in some digital cryptography processes, for example the AES process , also called "Rijndael" by and after its developers. It is used in the shift cipher in its elementary form, but not at the bit level but on the basis of an alphabet .
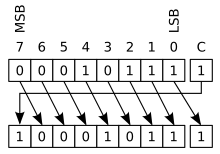
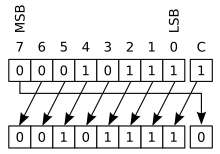
Cyclical shift with carry bit
Cyclic shift with carry bit (Eng. Rotate through carry ) works similarly to cyclic shift without carry bit , but the two ends of the register are treated as if they were separated by the carry bit. The carry bit is shifted into the register, the bit shifted out of the register becomes the new carry bit.
A single cyclic shift with a carry bit can simulate a logical or arithmetic shift by one place if the carry bit is set accordingly beforehand. For example 0, if the carry bit contains one , the shift to the right corresponds to an arithmetic shift to the right. For this reason, some microprocessors such as the PICmicro only implement commands for the two cyclic shift operations; there are no special commands for arithmetic or logical shifts.
Cyclic shifting with carry bits is particularly useful when shifting numbers that are larger than the word length of the processor, because the number is then stored in two registers and the bit shifted out of one register must be shifted into the other register. In the case of cyclical shifting with a carry bit, this bit is "stored" in the carry bit with the first shift and passed on with the next shift, without the need for additional instructions.
Shift operators in programming languages
C and C ++
In C, C ++, and related languages, the displacement operators are represented by <<and >>. The number of shifts is transferred as the second operand. Example:
x = y << 2;
assigns xthe result of the bit-wise shift of ytwo places to the left to the variable . This leads to the same result as x = y * 4.
In C and C ++, unsigned value calculations use logical shifts; Calculations with signed values behave depending on the implementation ( implementation-defined behavior ), provided the right operand is negative, the sign changes due to a left shift or a negative value is subjected to a right shift.
The result is also undefined according to the C and C ++ language standard if the number of bit shifts is greater than or equal to the bit width of the arithmetic architecture. For example, if you are working on a 32-bit architecture of Intel processors (IA32), a shift by 32 digits often does not change the result at all. H. for x = y << 32results x == y. The reason is in the way the compilers translate the shift operation into machine code. Most processors have direct instructions for shifting bits, with the number of shifts being encoded in the machine instruction only to a limited extent. For IA32 are e.g. B. 5 bit positions are provided to store the number of shifts. Therefore, only shifts in the range 0 to 31 can be performed correctly. Corresponding restrictions may also exist for other architectures and data types.
Java
In Java , all integer data types are signed, and the <<and operators >>perform arithmetic shifts. In Java there is also the operator >>>that performs a logical right shift. Since logical and arithmetic left shifts are identical, there is no <<<operator.
ARM assembler
In ARM assembler that displacement by operators are LSL( L ogical S hift L eft) LSR( L ogical S hift R ight) and ASR( A rithmetic S hift R ight), respectively. For the cyclic shifts, there are two commands ROR( RO tate R ight without carry) and RRX( R Otate R ight e X tended, with carry).
Applications
Although computers often have built-in efficient instructions for performing arithmetic and logical operations, all of these operations can also be performed by combinations of bitwise operators and zero comparisons. The following pseudocode shows, for example, as any two integers aand busing only shifts and adds can be multiplied:
c := 0
solange b ≠ 0
falls (b und 1) ≠ 0
c := c + a
schiebe a um 1 nach links
schiebe b um 1 nach rechts
return c
The code performs a written multiplication in the binary system, but in the unusual order from back to front (starting with the last digit of b).
See also: Written multiplication in the binary system
See also
Web links
- Division by bitwise shift (English)
Individual evidence
- ↑ ISO / IEC standard "C programming language" , Section 6.5.7 # 5 (English)
- ↑ A7.8 Shift Operators, Appendix A. Reference Manual, The C Programming Language
- ↑ SAL, SAR, SHL, SHR - Shift, Chapter 4. Instruction Set Reference, IA-32 Intel Architecture Software Developer's Manual