Flip-flop
A flip-flop (also flip-flop ), often bistable flip-flop or bistable flip-flop called, is an electronic circuit has the two stable states of the output signal. The current status depends not only on the currently available input signals, but also on the status that existed before the point in time considered. There is no dependence on time, only on events.
Due to the bistability , the multivibrator can store a data volume of one bit for an unlimited time. For this, unlike with non-volatile data memories , the power supply must be guaranteed at all times. As a basic component of sequential circuits, the flip-flop is an indispensable component of digital technology and therefore a fundamental component of many electronic circuits from quartz clocks to microprocessors . In particular, as an elementary one-bit memory, it is the basic element of static memory modules for computers.
history
The flip-flop circuit was discovered by the Englishmen William Henry Eccles and Frank W. Jordan on feedback tube amplifiers in search of counting circuits; on June 21, 1918 patent GB 148,582 was applied for. It was originally called the Eccles-Jordan circuit.
Characteristic
Flip-flops differ among other things
- in the number and the logical function of their inputs (described by their characteristic equation or function table ),
- in the time response to the input signals (data and control signals), in particular to the clock signals ( timing ),
- in the permeability of data signals to the output (transparency or instantaneous release)
- and in the structural design (simple internal positive feedback (single store flip-flop) or master-slave principle (two-store flip-flop)).


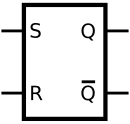
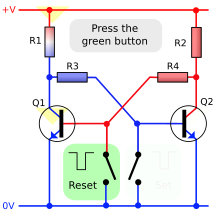
What they all have in common, however, is that they have two stable states that can be determined at an output. These states are "set" ( set ) and "reset" ( reset ) called. Signals at the inputs can be used to switch between these states. In addition to output Q, there is usually another output Q at which the negated value of Q is present. The switch-on state is not defined for a simple flip-flop consisting of two symmetrically arranged bipolar transistors (as in the picture on the right). This can be set using a capacitor at one of the two inputs.
For a flip-flop in standard TTL technology with 5 V operating voltage, a voltage to “ground” of 2.4 to 5 V (H level, HIGH ) at output Q means the status “set”. A voltage of 0 to 0.4 V (L level, LOW ) is then applied to the negated output Q. When using positive logic , this state is interpreted as Q = 1 and Q = 0. In the "reset" state, the voltages and logic values are interchanged at the outputs (Q = 0 and Q = 1). The L level can just as well be viewed as “set”, which stands out from an initial state with an H level - this is called negative logic . What is used is a matter of definition; Depending on the situation, one or the other of the stipulations may be appropriate. However, the negative logic is not emphasized within this article.
The simplest flip-flop is the non-clocked RS flip-flop; it has two entrances called S and R. The output of the flip-flop can switch to the "set" state via input S (or remain in this state if it is already "set"). The flip-flop can switch to the "reset" state via input R. The characteristics of the RS flip-flop and other types of flip-flops are discussed in more detail below.
By interconnecting several flip-flops, powerful systems such as registers , counters ( asynchronous or synchronous ), data memories ( semiconductor memories ) and microprocessors are created . Flip-flops are basic building blocks for all digital technology and microelectronics including the computer .
Classification based on cycle dependency
Non-clocked flip-flops
The state of the unclocked RS flip-flop introduced above is determined directly by the levels of the input signals S and R. Such flip-flops are called asynchronous level-triggered (Engl. Level triggered ) flip-flops. But there is also the possibility that a flip-flop changes its state only during a level change of the input signals and the level of the input signal itself has no further influence. Such flip-flops are called asynchronous edge-triggered flip-flops. Differentiators were previously used for practical implementation . Nowadays, the signal edges are usually converted internally into short needle pulses with the help of time differences, or they are evaluated directly by volatile internal states.
Clock controlled flip-flops
Since the input signals are stable only in certain time segments, it is often desirable that a flip-flop only reacts to the input signals at certain times. This behavior can be implemented by using a clock signal that enables the control inputs of the flip-flop for certain events. Taking a clock signal into account enables synchronization with other circuit parts and the formation of synchronous circuits . A distinction must be made here between how a flip-flop takes clock signals into account. The following figure shows how different types of flip-flops depend on each other.
Clock status and clock edge controlled flip-flops
Clock-controlled flip-flops are used as storage elements in synchronous switching mechanisms. They take their data and control signals through a (within the respective switching mechanism) standardized clock synchronization and can be in clock-state-controlled and edge-controlled divided flip-flops.
- Simple clock state controlled flip-flops react to the input signals from the beginning edge of a clock pulse up to its end edge. They are passed on to the exit, including their changes. Such modules controlled by 1-level or 0-level are transparent and do not tolerate any reaction of the output on its own input. The status at the end of the clock pulse is "caught" and stored. This is what gives the flip-flop, especially in English-language literature, the name latch (which translates as "bolt" or "door catch").
- If the status of this transparent “master flip-flop” is transferred to another, the “slave flip-flop”, with the end edge of the clock pulse, the status is separated from the inputs. Only the slave is connected to the output; its state is therefore not transparent. This creates a “classic” master-slave flip-flop with feedback capability , which can be used as a counting flip-flop .
- Edge-triggered flip-flops can only change their state during a specified clock edge. Pulses that contain such edges can change from the 0 level to the 1 level and return to the 0 level, that is, start with a rising edge; In other cases, they can go from the 1 level to the 0 level and back to the 1 level again, that is to say they can start with a falling edge (as in the figure "Bistable transistor multivibrator"). The clock edge-controlled flip-flop only reacts to the signals that are present at the inputs for a very short time after the specified clock edge. For the rest of the time until the next edge in the same direction, the previously set state is saved and - in contrast to state-controlled flip-flops - does not change even if the input signals change. A distinction is made between single - edge - controlled flip-flops that change on a rising (positive) clock edge or on a falling (negative) clock edge, as well as two- edge- controlled (acceptance at the input with one clock edge, output with the other clock edge).
Flip-flop types
RS flip-flop
An RS flip-flop (reset-set flip-flop), also called an SR flip-flop, is the simplest type of flip-flop. The basic element of this circuit is a bistable multivibrator without clock control, as shown in the first line of the table below. It has two inputs, commonly referred to as R and S. With suitable additional circuitry, both clock level-controlled RS flip-flops and clock-edge-controlled RS flip-flops can be generated from this. Then there is a third input, typically labeled C (clock), to which a clock signal can be applied. These RS flip-flops serve as basic circuits for building larger flip-flops.
Let the basic element of two logic gates (as shown above) have an idle state with R = S = 0. With a signal S = 1 at the “set” input and at the same time R = 0, the output Q of the flip-flop is set to “logical 1”. With the withdrawal of this request by S = 0 and at the same time R = 0, the flip-flop remains in the previously set state as a result of the feedback of the output to the input gate; so it is saved. Only when the “reset” input is activated with R = 1 and S = 0, the flip-flop is reset: Q = 0 arises at the output. Again, the status does not change when the request is withdrawn. The output signal in the case of R = S = 0 is uncertain if the previous course is not known.
The characteristic equation is (based on the circuit with NOR gates)
This equation cannot be resolved for Q with the means of formal logic, which characterizes the storage behavior: The output signal depends on its previous history.
The case of contradiction is critical if “set” and “reset” are requested at the same time with R = S = 1 or R = S = 0. This contradicting (therefore often referred to as “forbidden”) state leads to A 0 is created at the two outputs Q and Q for the RS flip-flop made of NOR gates, whereas a 1 at Q and Q for the RS flip-flop made of NAND gates. With industrial control systems , precautions must be taken in the event that the contradiction occurs in the event of operational disruptions. To do this, it must be considered which of the two requirements “set” and “reset” leads the system to a safe state, i.e. who should have priority. The output Q is set to Q = 1 in the circuit with NAND gates; this output has priority. In the circuit with NOR gates, Q = 0 is established; this output has reset priority.
It is often said that the state R = S = 1 is unstable or indeterminate; in fact, this state is completely stable. Only the successor state is indeterminate when the (almost) simultaneous switch to the memory state with R = 0 and S = 0. Then a metastable state can occur, the maximum duration of which cannot be guaranteed. When implementing RS flip-flops in software in programmable logic controllers , the order in which the commands are entered must be observed. The command executed last becomes the dominant one in program processing. Within multitasking systems, the processing of setting and resetting must therefore be encapsulated and must not be interrupted. Dominant RS flip-flops as individual hardware components were not available. Dominance was only used indirectly when a complex module was equipped with reset and set inputs.
The mode of operation of an RS tipping stage can be compared to that of a mechanical rocker, the center of gravity of which is higher than the pivot point. This structure creates positive feedback as in the gate circuit; the rocker then takes one of two possible stable end positions without it being clear beforehand which it will be. However, it can be brought into one or the other desired end position indefinitely by pushing it. A central position is not possible in a binary system. (Remaining in unstable equilibrium - as can be achieved with difficulty with the coupled rocker due to friction - is not necessary with the flip-flop.)
In the following compilation, the upper section is designed with negated characters S and R at the entrance. This means that the idle state of the input signals is formed by the 1 level and the active, switching state by the 0 level of the inputs. This is due to the construction of the flip-flop from NAND gates and is quite common in practice. This applies in particular to TTL modules, where an open input behaves as if it were set to 1 level. In the lower section, the inputs are negated by the release level, so that here the non-negated characters are used again. The signal-time diagrams are drawn for positive logic: A 1 level is represented by the upper state (HIGH), a 0 level by the lower (LOW).
| Name and symbols | Signal-time diagram | circuit diagram | Function table | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Asynchronous RS flip-flop
|
Standard behavior when equipped with negated inputs
|
Logic circuit of an RS flip-flop made up of two NAND gates
|
|
||||||||||||||||||||||||||||
RS flip-flop with clock level control
|
Behavior when R and S are enabled by 1 level at E or C with clock
|
Logic circuit of a clocked RS flip-flop made up of four NAND gates
|
|
||||||||||||||||||||||||||||
D flip-flop
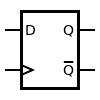
Edge-triggered D flip-flop
The D flip-flop (abbreviated for data or delay flip-flop) is used to delay the signal at the data input until it is enabled, synchronously with a clock edge. It has a data input D and a dynamic input C (clock), which is marked with in the circuit symbol if it reacts to a rising edge. (If a falling edge is the active one, a negation character is placed in front of it outside the symbol contour.) This D flip-flop realizes the elementary characteristic function of the clock-controlled direct transfer of the data input to the output
Here, D applies to the state up to the triggering and Q 'after the triggering. The current status is held ("delayed") until the next active clock edge. The opposite flank has no influence.
This behavior leads to two important uses:
- Storage of a data bit until the clock input triggers a new storage and
- Synchronization of parallel, simultaneously started processes that are subject to different delay times depending on the number and type of components run through .
Because all changes to D that occur after the active edge only have an effect on the next active edge, it is non-transparent and, as an elementary flip-flop, has direct feedback . For example, a connection from output Q to input D of the same flip-flop is permitted, through which the output signal changes to its opposite, but always only on the next active clock edge. This makes the D flip-flop suitable as a basic component in counting circuits. By combining several such flip-flops and external circuitry, extensive circuits such as synchronous counters , frequency dividers or shift registers can be implemented - as with other clock edge-controlled flip-flops .
With a clock enable input CE (in German-speaking countries “preparation input” V), the clock input can be enabled in its function ( enable = release); without enabling, the status remains unchanged until a later clock edge. In this configuration, the flip -flop is referred to as a DV flip-flop .
Clock level controlled D flip-flop
Alternatively, in addition to the data input D, D flip-flops can contain a static input E that reacts to levels. This flip-flop is a typical latch . The specified function table applies for this. Here, X means any logic level and Q 0 means the last D level before E = 0.
The D-Latch consists of an RS flip-flop and an unbalanced input circuit in front of it. With this the "forbidden" state R = S = 1 is avoided. As long as the release input (usually connected to the clock) is set to E = 1, the data at input D appear directly at output Q. In this state, the D-latch is transparent . The data bit remains available for the remainder of a clock period, while the input signal can already change.
| Name and symbols | Signal-time diagram | circuit diagram | Function table | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Level controlled D flip-flop 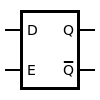
|
Acceptance of the input information as long as 1 level at E
|
D-Latch in NAND implementation
|
|
|||||||||||||||
JK flip-flop
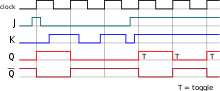
JK flip-flops were likely named after Jack Kilby ; occasionally they are called jump / kill flip-flops. They are based on the asynchronous RS flip-flop, but are edge-controlled or designed as master-slave flip-flops. With the clock signal and the input assignment J = 1 and K = 0, a 1 is generated and stored at the output, alternatively a 0 for K = 1 and J = 0. The state J = K = 1 is permitted; in this case the output level changes with every effective edge of the clock signal. This behavior allows the designation as a toggle flip-flop. For J = K = 0 the last initial state is retained. The characteristic equation is (with J, K, Q up to the edge and Q 'after the edge)
When the JK flip-flop is implemented as a master-slave flip-flop controlled by the clock state, the main restriction that must be observed is that the states of the two inputs J and K may no longer change during the transparency phase of the master . This means that there is no purely state-controlled flip-flop. This disadvantage is one reason why they are rarely used as master-slave flip-flops in more complex digital circuits and are replaced by edge-triggered flip-flops, which do not have this disadvantage.
When the JK flip-flop is implemented as an edge-controlled flip-flop, input C can be designed for rising edges (change from 0 to 1) or for falling edges (change from 1 to 0).
| Name and symbols | Signal-time diagram | circuit diagram | Function table | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Edge-triggered JK flip-flop |
Acceptance of the input information by a rising edge at C (clock) |
S = 0 or R = 0 can only be achieved as long as an edge that occurred at C runs through the 3 non-gates |
|
|||||||||||||||||||||
T flip-flop
Synchronous T flip-flop
In addition to the dynamic C clock input, the synchronous T flip-flop has a T input. T stands for toggle - switching back and forth. It shows an alternating behavior synchronous to the active edge whenever and only when T = 1. It can be formed from an edge-triggered JK flip-flop by connecting the J and K inputs and acting together as a T input. The synchronous T flip-flop is used in synchronous counters, for example . Its behavior is described by the table provided. Q n means the state of the flip-flop at output Q after the nth active clock edge.
| Name and symbols | Signal-time diagram | circuit diagram | Function table | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Synchronous T flip-flop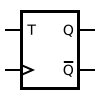
|
|
Like edge-triggered JK flip-flop with J = K = T |
|
||||||||||
Asynchronous T flip-flop
If the T input is permanently set to "1", the previous clock input C takes on the function of a signal input. Since there is no connection to a clock, this version is referred to as an asynchronous T flip-flop. Although the input signal does not have to occur periodically, it is sometimes also called a clock signal.
The first implementation of a toggle flip-flop in electromechanical module form was introduced as an impulse switch for the push button circuit (staircase switching without time switch function) and is still widely used in new installations. The asynchronous T-flip-flop can be formed by a clock edge-controlled D-flip-flop if its output Q is fed back to the input D. A clock state-controlled version shows the next picture in which the master (left RS-FF) is assigned the returned output signal while C = 1; as long as the input of the slave (right RS-FF) is blocked. With C = 0 the input of the master is blocked and the slave is assigned the status of the master. The signal at Q changes with a falling edge.
With a periodic input signal, the output signal is halved by switching back and forth (frequency division by 2); accordingly, these flip-flops are primarily used as a basic element in asynchronous binary counters and in decimal frequency dividers and frequency counters . They are also used when a square wave signal with a duty cycle of exactly 50% is to be obtained, when only an asymmetrical signal, but at twice the frequency, is available.
Additional asynchronous control inputs for flip-flops
Depending on the design, the clocked flip-flops (clock status and clock edge-controlled flip-flops) have additional inputs for asynchronous control signals. These influence the flip-flop independently of the clock signal. Depending on the design, these components have an additional reset input R, a set input S or both. The reset is sometimes referred to as “ Clear ”, the setting as a “Preset”. Frequently, the two additional inputs to LOW-active control can be designed and then with S and R , respectively.
The asynchronous reset input can be used to bring the flip-flop to the initial state Q = 0 (reset state). This function is used, for example, when switching on the supply voltage or when the circuit has to be brought back to the initial state during operation. The behavior of the set input corresponds to the reset input, but brings the flip-flop into the set state Q = 1. Simultaneous actuation of the asynchronous set and reset inputs is referred to as a "prohibited" state .
Timing the flip flops
In the case of time-critical applications of the flip-flop components in electronic circuits, various specifications must be observed. A clock-edge-triggered D flip-flop with single-edge triggering is considered here as an example. The active switching edge of the clock (Clk) is used as a reference for each individual switching process.
The input signal (data) of the flip-flop must not change for a defined minimum duration before the active switching edge of the clock signal. This time is a setup time (Engl. Setup-time ), respectively. Accordingly, the logic state at the D input must also not change for a defined minimum duration after the active switching edge of the clock signal. This time is referred to as the hold-time. Until after the edge, the output signal has set, the signal propagation time (engl. Through the device propagation delay time ) to be observed.
The guaranteed frequency of the clock signal must not be exceeded. Furthermore, the minimum pulse width of the clock signal must not be undershot. This is counted from the active clock edge to the opposite clock edge of the pulse. In the case of flip-flops with additional asynchronous control inputs, the control signals must not change for a defined minimum time before the active clock edge of the clock signal and for a defined minimum duration afterwards. If the timing requirements are not adhered to, it can be assumed that the flip-flops will malfunction.
All other flip-flops with clock input basically have the same behavior as the D flip-flop. With the JK flip-flop, the setup and hold times for the J and K input must also be observed. Time specifications also apply to the RS flip-flop.
Use of flip flops
In the applications listed above and for the individual types, flip-flops are typically part of a larger electronic component. In professional circuit development, flip-flops are rarely used as individual components. Typically, components are used which, in addition to flip-flops, consist of other circuit functions in a common component. This includes FPGA , PLD and ASIC components. These components typically contain D-type flip-flops.
Discrete circuits
In addition to the flip-flops and monoflops, the following table also contains the function-related latches and bus interfaces.
| Type | FF art | Logic family / series | description | PINs | Voltage range |
|---|---|---|---|---|---|
| 74ACT74 | 74xx | ||||
| 74HCT73 | 74xx | 4.5-5.5V | |||
| 74HC374 | D. | 74xx | 8 × D flip-flops | 2-6 V | |
| 74HC377 | D. | 74xx | 8 × D flip-flops | 2-6 V | |
| 74HCT377 | D. | 74xx | 8 × D flip-flops | 4.5-5.5V | |
| 74AC74 | D. | 74xx | 2 × D flip-flops | 2-6 V | |
| 4027 | JK | CMOS : 4000 | 2 × JK flip-flops | 3-18 V | |
| 7429 | TTL | ||||
| 4095 | JK | CMOS : 4000 | JK master-slave flip-flop | ||
| 4096 | JK | CMOS : 4000 | JK master-slave flip-flop | ||
| 4003 | D. | CMOS : 1/4000? | 8-bit addressable latch | ||
| 4013 | D. | CMOS : 4000 | 2 × D flip-flops | 3-18 V | |
| 4042 | D. | CMOS : 4000 | 4 × latch | ||
| 4043 | D-latch | CMOS : 4000 | 4 × NOR-RS latch | ||
| 4044 | D-latch | CMOS : 4000 | 4 × NAND-RS latch | ||
| 4076 | D-latch | CMOS : 4000 | 4 × D-Latch | ||
| 4099 | D-latch | CMOS : 4000 | 8-bit addressable latch | 3-15V | |
| 4508 | D-latch | CMOS : 4000 | 2 × 4-bit latch | ||
| 4047 | Monoflop | CMOS : 1/4000? | monostable / astable multivibrator | ||
| 4098 | Monoflop | CMOS : 1/4000? | 2 × monostable multivibrator | ||
| 4099 | D. | CMOS : 4000 | 2 × monostable multivibrator | 3-15V | |
| 4528 | Monoflop | CMOS : 4000 | 2 × monostable multivibrator | ||
| 4538 | Monoflop | CMOS : 4000 | 2 × monostable multivibrator (precision type) | ||
| 4723 | D-latch | CMOS : 4000 | 2 × addressable 4-bit latch | ||
| 4724 | D-latch | CMOS : 4000 | addressable 8-bit latch | ||
| 40174 | D. | CMOS : 4000 | 6 × D flip-flop with master reset | 3-15V | |
| 40175 | D. | CMOS : 4000 | 4 × D flip-flop with master reset | 3-15V | |
| 40373 | D-latch | CMOS : 4000 | 8 × latch | ||
| 40374 | D. | CMOS : 4000 | 8 × D flip-flops | ||
| 4548 | Monoflop | CMOS : 4000 | 2 × monoflop | ||
| 74107 | JK | CMOS : 7400 | 2 × JK flip-flop with clear, edge-triggered / pulse-triggered | ||
| 74109 | JK | CMOS : 7400 | 2 × JK flip-flop with clear and preset, edge triggered | ||
| 74112 | JK | CMOS : 7400 | 2 × JK flip-flop with clear and preset, edge triggered | ||
| 74113 | JK | CMOS : 7400 | 2 × JK flip-flop with preset, edge triggered | ||
| 74114 | JK | CMOS : 7400 | 2 × JK flip-flop with clear and preset, edge triggered | ||
| 7473 | JK | CMOS : 7400 | 2 × JK flip-flop with clear, edge-triggered / pulse-triggered | ||
| 7476 | JK | CMOS : 7400 | 2 × JK flip-flop with clear and preset, edge-triggered / pulse-triggered | ||
| 7478 | JK | CMOS : 7400 | 2 × JK flip-flop with clear and preset, edge-triggered / pulse-triggered | ||
| 74279 | RS latch | CMOS : 7400 | 4 × latch | ||
| 7477 | D-latch | CMOS : 7400 | 4 × latch, not inverting | ||
| 74373 | D-latch | CMOS : 7400 | 8 × latch, not inverting | ||
| 74573 | D-latch | CMOS : 7400 | 8-bit bus interface, not inverting | ||
| 74841 | D-latch | CMOS : 7400 | 10-bit bus interface, not inverting | ||
| 74843 | D-latch | CMOS : 7400 | 9-bit bus interface, not inverting | ||
| 74845 | D-latch | CMOS : 7400 | 8-bit bus interface, not inverting | ||
| 74533 | D-latch | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74533 | D-latch | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74563 | D-latch | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74846 | D-latch | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74844 | D-latch | CMOS : 7400 | 9-bit bus interface, inverting | ||
| 74842 | D-latch | CMOS : 7400 | 10-bit bus interface, inverting | ||
| 74563 | D-latch | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 7475 | D-latch | CMOS : 7400 | 4 × D-Latch with complementary outputs | ||
| 74375 | D-latch | CMOS : 7400 | 4 × D-Latch with complementary outputs | ||
| 74173 | D. | CMOS : 7400 | 4 × D flip-flop, non-inverting | ||
| 74174 | D. | CMOS : 7400 | 6 × D flip-flop, non-inverting | 3-15V | |
| 74378 | D. | CMOS : 7400 | 6 × D flip-flop, non-inverting | ||
| 74273 | D. | CMOS : 7400 | 8 × D flip-flop, non-inverting | ||
| 74374 | D. | CMOS : 7400 | 8 × D flip-flop, non-inverting | ||
| 74377 | D. | CMOS : 7400 | 8 × D flip-flop, non-inverting | ||
| 74534 | D. | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74564 | D. | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74576 | D. | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74821 | D. | CMOS : 7400 | 10-bit bus interface, not inverting | ||
| 74822 | D. | CMOS : 7400 | 10-bit bus interface, inverting | ||
| 74823 | D. | CMOS : 7400 | 9-bit bus interface, not inverting | ||
| 74824 | D. | CMOS : 7400 | 9-bit bus interface, inverting | ||
| 74825 | D. | CMOS : 7400 | 8-bit bus interface, not inverting | ||
| 74826 | D. | CMOS : 7400 | 8-bit bus interface, inverting | ||
| 74173 | D. | CMOS : 7400 | 4 × D flip-flop, non-inverting | ||
| 74175 | D. | CMOS : 7400 | 4 × D flip-flop, complementary outputs | ||
| 74379 | D. | CMOS : 7400 | 4 × D flip-flop, complementary outputs | ||
| 7474 | D. | CMOS : 7400 | 2 × D flip-flop, complementary outputs | ||
| 74221 | Monoflop | CMOS : 7400 | Monoflop with Schmitt trigger input | ||
| 74123 | Monoflop | CMOS : 7400 | 2 × triggerable monoflop | ||
| 74423 | Monoflop | CMOS : 7400 | 2 × triggerable monoflop | ||
| D172 (SN7472) -DDR- | JK | TTL | JK master-slave flip-flop with 3 J and 3 K inputs each | ||
| D174 (SN7474) -DDR- | D. | TTL | 2 × D flip-flop, positive edge triggered | ||
| D175 (SN7475) -DDR- | D. | TTL | 4 × D flip-flops (catch flip-flops) | ||
| D274 (SN74 H 74) -DDR- | D. | TTL | 2 × D flip-flop, positive edge triggered, high-speed TTL version | ||
| D L 112D (SN74 LS 112N) -DDR- | JK | LS-TTL (lower operating voltage and level than TTL) | 2 × JK flip-flop, edge-triggered, S- u. R input, max. Clock frequency 30MHz | ||
| U103D -DDR- | "RST" | "P-MOS" | "RST flip-flop" (?) | ||
| U108D -DDR- | JK | "P-MOS" | 2 × JK flip-flops | ||
| V4013D (CD4013) -DDR- | D. | CMOS | 2 × master-slave D flip-flop, max. Clock frequency> 3.5 / 8 / 12MHz at 5/10 / 15V | 3-18 V | |
| V4027D (CD4027) -DDR- | JK | CMOS | 2 × JK flip-flop, max. Clock frequency like V4013D | ||
| V4044D (CD4044) -DDR- | RS flip-flop (latch) | CMOS | 2 × RS flip-flop (latch), delay time to the output 300/140 / 100ns at U = 5/10 / 15V | ||
| SN74LS74 | D. | 74xx | 2 × D flip-flops | 4.75-5.25V | |
| LS76 | JK | LS-TTL (lower operating voltage and level than TTL) | 2 × JK flip-flops | 4.75-5.25V | |
| LS112 | JK | LS-TTL (lower operating voltage and level than TTL) | 2 × JK flip-flops | 4.75-5.25V | |
| LS273 | D. | LS-TTL (lower operating voltage and level than TTL) | 8 bit | 4.75-5.25V |
literature
- Manfred Seifart, Helmut Beikirch: Digital circuits . Verlag Technik, Berlin 1998, ISBN 3-341-01198-6 .
- Gerd Scarbata: Synthesis and Analysis of Digital Circuits . Oldenbourg Wissenschaftsverlag GmbH, Munich 2001, ISBN 3-486-25814-1 .
- Manfred Seifart: Digital circuits . Verlag Technik, Berlin (GDR) 1986, ISBN 3-341-00148-4 (Chapter: 5.3 Flip-flop stages, p.126 / 5.3.1 Working principle, basic flip-flop, p.126 / 5.3.2 Clocked flip-flops, p.128 / 5.3 .3 Counting flip-flops (buffer storage flip-flops) p.128 / 5.3.4 Systematics of the flip-flop stages p.129 / 5.3.4.1 Differentiation with regard to the mode of operation of the clock pulse (inputs p.129 / clock control p.129 / clock edge-controlled counting flip-flops S.130, edge-triggered flip-flops, master-slave flip-flops S.131, frequent flip-flop types and their logic behavior (Table 5.5 S.132-133) /5.3.4.2 Differentiation with regard to the logical behavior S.134 (including conversion a flip-flop type into another type by connecting logic elements or returning the outputs to the inputs: / univibrators (monoflops) p.135-142 / table5.6 on p.136 / table 5.4 p.126 some GDR flip-flop circuits )).
- Gerhard Ruder: "cmos1 digital` 84/85, data dictionary and comparison table for integrated circuits ". ECA GmbH Munich, 1985, ISBN 3-88109-025-8 ( inter alia, functional table of contents flip-flops pp. "1-3").
- Edgar Gaßner, Max Reidl: "cmos4000, data dictionary and comparison table for integrated circuits". ECA GmbH Munich, 1990, ISBN 3-88109-040-1 (including functional table of contents flip-flops, pp. "1-4").
- Edgar Gaßner, Max Reidl: "cmos7400, data dictionary and comparison table for integrated circuits". ECA GmbH Munich, 1991, ISBN 3-88109-050-9 (including a functional table of contents for flip-flops, pp. "1-13" to "1-14").
Web links
- Wikibooks - digital circuit technology on the subject of flip flops
- Interactive flip-flops (Java required)
- Interactive simulation of different flipflop types with the Hades simulation framework (English)
- Interactive LogiFlash animations (Chapter 5, requires Flash)
- More information on RS and JK flip-flops (homepage German / English)
Individual evidence
- ↑ DIN EN 60617–12 Graphic symbols for circuit diagrams - Part 12: Binary elements. April 1999, German translation of the international standard IEC 60617–12: 1997
- ^ The Radio Review. Dec. 1919 , p. 143 ff.
- ↑ On the history: Robert Dennhardt: The flip-flop legend and the digital: a history of the digital computer from break contact to tube electronics 1837–1945 . Kulturverlag Kadmos, Berlin 2009, Simultaneously: Diss. Humboldt University, Berlin 2007, ISBN 978-3-86599-074-7 .
- ↑ Wolfram Schiffmann, Robert Schmitz: Technical Computer Science 1: Fundamentals of digital electronics . Springer-Verlag, 2013, ISBN 978-3-642-18894-7 , pp. 240 .
- ↑ F. Dokter, J. Steinhauer: Digital electronics in measurement technology and data processing - Volume II. 3rd edition Philips reference books, 1973, ISBN 978-3-87145-273-4 , p. 21
- ↑ Erwin Böhmer: Elements of Applied Electronics. 9th ed. Vieweg, 1994, ISBN 978-3-528-94090-4 , p. 251.