Asynchronous counter

A ripple ( English Ripple Counter ) is an electrical component of the digital technology , which is one of a series of events. Each resulting number is saved until the next event. In the simplest case, the counter reading is represented in numbers of the dual system . In this case, the possible numbers are limited to the number of binary storage elements present . One then speaks of n-bit asynchronous counters . With suitable switching, counters such as frequency dividers in the decimal system are also possible and widely used. The input signal to be counted is also referred to as a clock signal in the case of a periodic sequence . ${\ displaystyle n}$ ${\ displaystyle \ left [0; \, 2 ^ {n} -1 \ right]}$

Asynchronous counters belong to the group of asynchronous circuits because only the first storage element changes at the time of a fixed (rising or falling) edge of an input signal; any changes that may be required in other storage elements follow with delay times in the logic and storage elements. With conventional electronic counters for visual display of the counter reading, the delay time is insignificant compared to the human reaction time.

construction

Asynchronous 4-bit up-counter from T-flip-flops

An asynchronous counter can be constructed from T flip-flops , for example in the diagram opposite. A T flip-flop changes its output state from the current state exactly when an active edge occurs at its input. The circuit is drawn for flip-flops that react to a falling clock edge, i.e. H. every flip-flop is negative edge triggered. At all other times it retains the current initial state.

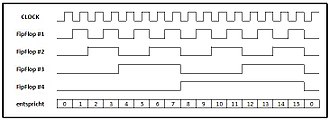
In the asynchronous counter, the input of the first flip-flop is connected to the signal of the event to be counted. If the edge that is active for the flip-flop occurs in this signal, the level at output Q _{0 changes} , i.e. from low to high or from high to low. After every two active edges at the input, a rectified edge occurs at the output. For each flip-flop, the number of level changes at the output is 2: 1 less than at the input. When several T-flip-flops are connected in series ( cascading ), this division ratio becomes exponentially greater, in the case of flip-flops. ${\ displaystyle 2 ^ {n}: 1}$ ${\ displaystyle n}$

Due to the wiring shown of the inputs of the flip-flops, their output signals can be understood as a sequence of digits. In the example, each output represents the digit of a four-digit binary number, with Q ₀ in the least significant place. The following table shows the counting process. With each active edge, the count increases in the order of the natural numbers. If the inverted outputs are combined, the circuit counts down. With other circuits, for example, four flip-flops can be used to represent the 8-4-2-1 code of a decimal digit, see frequency divider . This group of four shares a ratio of 10: 1. Multi-digit decimal numbers can be formed with several groups in a row. A decimal number is always required for the visual output of a meter reading to humans.

Instead of T flip-flops, JK flip -flops can basically also be used if these are set to the toggle state by J = 1 and K = 1.

Signal-time diagram of an up-counter with 4 flip-flops (without gate delay times) when triggered on a falling edge

Q ₃	Q ₂	Q ₁	Q ₀	Binary value	Decimal value
0	0	0	0	0000	0
0	0	0	1	0001	1
0	0	1	0	0010	2
0	0	1	1	0011	3
0	1	0	0	0100	4th
0	1	0	1	0101	5
0	1	1	0	0110	6th
0	1	1	1	0111	7th
1	0	0	0	1000	8th
1	0	0	1	1001	9
1	0	1	0	1010	10
1	0	1	1	1011	11
1	1	0	0	1100	12
1	1	0	1	1101	13
1	1	1	0	1110	14th
1	1	1	1	1111	15th
0	0	0	0	0000	0

properties

Asynchronous counters are often simpler in structure than synchronous counters, on the other hand slower. They are particularly suitable for processes that are subject to observation. The human eye and conscious processing cannot follow faster processes.

In the synchronous counter, the flip-flops are supplied with the same clock signal in parallel; In the asynchronous counter, the signal is passed on serially through the flip-flops. Due to the internal running time of the components, there are delays in the asynchronous counter that add up component by component. When flip-flops are connected in series , the signal is delayed until the last flip-flop ${\ displaystyle t _ {\ mathrm {P}}}$ ${\ displaystyle n}$

{\ displaystyle t_ {n} = n \ cdot t _ {\ mathrm {P}}}

.

Example: If you start (guideline value for TTL blocks) and a 12-bit counter that is filled to the point of overflow in 2 s, the mean interval between two counting pulses is only about 0.05%. ${\ displaystyle t _ {\ mathrm {P}} = 20 {\ text {ns}}}$ ${\ displaystyle t_ {n}}$

At high frequencies, on the other hand, it may become impossible to read out a single counter reading at all. Because in the same counter, with an input frequency greater than 4 MHz, the cycle time is greater than the interval between two counting pulses. ${\ displaystyle t_ {n}}$

Applications

For applications in measurement technology and additional equipment, see frequency counters and universal counters .

literature

Tietze, Ulrich; Schenk, Christoph: Semiconductor circuit technology . 12th edition. Springer, 2002, ISBN 3-540-42849-6 .
Beuth, Klaus: Digital technology . 10th edition. Vogel, 1998, ISBN 3-8023-1755-6 .
Seifart, Manfred; Beikirch, Helmut: Digital circuits . 5th edition. Technology, 1998, ISBN 3-341-01198-6 .