Intermediate value theorem

Intermediate value theorem : Let there be a continuous function with defined on , then there is at least one with ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle f(a)<s<f(b)}$ ${\displaystyle x}$ ${\displaystyle f(x)=s}$

In real analysis , the intermediate value theorem is an important theorem about the range of values of continuous functions .

The intermediate value theorem states that a real function that is continuous on a closed interval takes any value between and . If in particular and have different signs , the intermediate value theorem guarantees the existence of at least one zero of in the open interval . This special case is known as the Bolzano zero set and named after Bernard Bolzano . On the other hand, the intermediate value record can also be derived from the zero position record. The two formulations are therefore equivalent. ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle f(a)}$ ${\displaystyle f(b)}$ ${\displaystyle f(a)}$ ${\displaystyle f(b)}$ ${\displaystyle f}$ ${\displaystyle (a,b)}$

sentence

Play media file

Formulation and intuition behind the intermediate value theorem

Let it be a continuous real function that is defined on a closed interval. Then for each (if ) or (if ) there is a with . In other words, with and means that . ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ ${\displaystyle u\in [f(a),f(b)]}$ ${\displaystyle f(a)\leq f(b)}$ ${\displaystyle u\in [f(b),f(a)]}$ ${\displaystyle f(b)<f(a)}$ ${\displaystyle c\in [a,b]}$ ${\displaystyle f\left(c\right)=u}$ ${\displaystyle m:=\min\{f(a),f(b)\}}$ ${\displaystyle M:=\max\{f(a),f(b)\}}$ ${\displaystyle [m,M]\,\subseteq \,f([a,b])}$

proof

The proof assumes that the boundaries of the closed interval considered are finite (equivalent: is also bounded and therefore compact .). In fact, the interim value theorem also applies to unlimited closed intervals; the assertions then to be proven can be found in the generalization section of this article. ${\displaystyle [a,b]}$ ${\displaystyle [a,b]}$

Without loss of generality applies , and it is . - The function ${\displaystyle f(a)<f(b)}$ ${\displaystyle u\in [f(a),f(b)]}$

${\displaystyle g\colon [a,b]\to \mathbb {R} ,\quad x\mapsto g(x)=f(x)-u}$

is (as a composition of second continuous functions) continuously on . ${\displaystyle [a,\,b]}$

Because of is because of is , in total ${\displaystyle f(a)\leq u}$ ${\displaystyle g(a)\leq 0}$ ${\displaystyle u\leq f(b)}$ ${\displaystyle 0\leq g(b)}$ ${\displaystyle g(a)\leq 0\leq g(b).\mathbf {(1)} }$

To prove the claim, it is sufficient to show that has a zero , because . ${\displaystyle g}$ ${\displaystyle c\in [a,\,b]}$ ${\displaystyle g(c)=0\Leftrightarrow f(c)=u}$

A sequence of intervals with the following properties (to be proven) is used to prove the existence of : ${\displaystyle c}$ ${\displaystyle ([a_{k},\,b_{k}]),\;k\in \mathbb {N} }$

• All links respect the chain of inequalities (1) (and therefore include ). ${\displaystyle [a_{k},b_{k}]}$ ${\displaystyle c}$ ${\displaystyle \mathbf {(i)} }$
• ${\displaystyle ([a_{k},\,b_{k}])}$is an interval nesting (and defines exactly one ). ${\displaystyle c\in [a,b]}$ ${\displaystyle \mathbf {(ii)} }$
• ${\displaystyle c}$is a zero of . ${\displaystyle g(x)}$ ${\displaystyle \mathbf {(iii)} }$

Let a sequence of intervals be defined recursively with for the first interval. ${\displaystyle ([a_{k},\,b_{k}]),\;k\in \mathbb {N} }$ ${\displaystyle a_{1}=a,\;b_{1}=b}$

${\displaystyle c_{k}={\frac {a_{k}+b_{k}}{2}}}$is the midpoint of the -th interval ${\displaystyle k}$ .

Let the limits of the following interval be ${\displaystyle [a_{k+1},\,b_{k+1}]}$

for : and ${\displaystyle g(c_{k})<0}$ ${\displaystyle a_{k+1}=c_{k},b_{k+1}=b_{k}}$

for : . ${\displaystyle g(c_{k})\geq 0}$ ${\displaystyle a_{k+1}=a_{k},b_{k+1}=c_{k}}$

to (i): With (1) is not positive, not negative. ${\displaystyle g(a_{1})}$ ${\displaystyle g(b_{1})}$

When changing from to , exactly one of the interval limits (or ) is replaced by a new limit if and only if it is not positive (or not negative). ${\displaystyle [a_{k},b_{k}]}$ ${\displaystyle [a_{k+1},b_{k+1}]}$ ${\displaystyle a_{k}}$ ${\displaystyle b_{k}}$ ${\displaystyle c_{k}}$ ${\displaystyle g(c_{k})}$

So for or , qed ${\displaystyle g(a_{k})\leq 0\leq g(b_{k})}$ ${\displaystyle {\boldsymbol {alle}}}$ ${\displaystyle a_{k}}$ ${\displaystyle b_{k}}$

to (ii): In the following interval the replacing limit is greater than a replaced lower limit , but smaller than a replaced upper limit , in that the center of the interval is from . Since the transition from to the interval diameter is halved, the interval diameter of almost all subsequent members is smaller than any given one. ( is a null sequence .) ${\displaystyle [a_{k},b_{k}]}$ ${\displaystyle [a_{k+1},b_{k+1}]}$ ${\displaystyle c_{k}}$ ${\displaystyle a_{k}}$ ${\displaystyle b_{k}}$ ${\displaystyle c_{k}}$ ${\displaystyle [a_{k},b_{k}]}$ ${\displaystyle [a_{k},b_{k}]}$ ${\displaystyle [a_{k+1},b_{k+1}]}$ ${\displaystyle d_{k}=b_{k}-a_{k}}$ ${\displaystyle \Leftrightarrow (d_{k})}$

Assertion : is monotonically increasing . ${\displaystyle (a_{k})}$ ${\displaystyle \Leftrightarrow \forall k:a_{k+1}\geq a_{k}.\mathbf {(2)} }$

Proof : There is nothing to prove for. For follows : . ${\displaystyle a_{k+1}=a_{k}}$ ${\displaystyle a_{k+1}=c_{k}}$ ${\displaystyle b_{k}>a_{k}}$ ${\displaystyle a_{k+1}={\frac {a_{k}+b_{k}}{2}}>{\frac {a_{k}+a_{k}}{2}}=a_{k}}$

Claim : is monotonically decreasing . ${\displaystyle (b_{k})}$ ${\displaystyle \Leftrightarrow \forall k:b_{k+1}\leq b_{k}.\mathbf {(3)} }$

Proof : There is nothing to prove for. For follows : . ${\displaystyle b_{k+1}=b_{k}}$ ${\displaystyle b_{k+1}=c_{k}}$ ${\displaystyle a_{k}<b_{k}}$ ${\displaystyle b_{k+1}={\frac {a_{k}+b_{k}}{2}}<{\frac {b_{k}+b_{k}}{2}}=b_{k}}$

Assertion : , is a null sequence. - Proof : The diameter of the interval is ${\displaystyle (d_{k})}$ ${\displaystyle d_{k}=b_{k}-a_{k}}$ ${\displaystyle \mathbf {(4)} }$ ${\displaystyle [a_{k+1},b_{k+1}]}$

for : ; ${\displaystyle g(c_{k})<0}$ ${\displaystyle d_{k+1}=b_{k+1}-a_{k+1}=b_{k}-c_{k}={\frac {2b_{k}}{2}}-{\frac {a_{k}+b_{k}}{2}}={\frac {b_{k}-a_{k}}{2}}={\frac {d_{k}}{2}}}$

for : . ${\displaystyle g(c_{k})\geq 0}$ ${\displaystyle d_{k+1}=b_{k+1}-a_{k+1}=c_{k}-a_{k}={\frac {a_{k}+b_{k}}{2}}-{\frac {2a_{k}}{2}}={\frac {b_{k}-a_{k}}{2}}={\frac {d_{k}}{2}}}$

All in all, all of them can also be written, and because of a (geometric) zero sequence. ${\displaystyle d_{k}}$ ${\displaystyle d_{k}=d_{1}\cdot \left({\frac {1}{2}}\right)^{k-1}}$ ${\displaystyle (d_{k})}$ ${\displaystyle \left|{\frac {1}{2}}\right|<1}$

With (2), (3) and (4) there is an interval nesting that defines exactly one number . ${\displaystyle ([a_{k},\,b_{k}])}$ ${\displaystyle c\in \mathbb {R} }$

With lies in the interval of the assumption, q. e. d. ${\displaystyle \forall k:[a_{k},b_{k}]\subset [a,b]\Rightarrow \{c\}=\bigcap _{k\in \mathbb {N} }[a_{k},b_{k}]\subset [a,b]}$ ${\displaystyle c}$

Comment : The numerical procedure bisection is based on a finite number of intervals of an interval nesting as constructed . ${\displaystyle ([a_{k},b_{k}])}$

to (iii): is the common limit of the sequences and ; because of continuity of is the common limit of the sequences and . The limitation of the consequences and causes that is neither positive nor negative. ${\displaystyle c}$ ${\displaystyle (a_{k})}$ ${\displaystyle (b_{k})}$ ${\displaystyle g(x)}$ ${\displaystyle g(c)}$ ${\displaystyle (g(a_{k}))}$ ${\displaystyle (g(b_{k}))}$ ${\displaystyle (g(a_{k}))}$ ${\displaystyle (g(b_{k}))}$ ${\displaystyle g(c)}$

From (ii) follows

${\displaystyle \lim _{k\to \infty }a_{k}=c=\lim _{k\to \infty }b_{k}}$,

therefrom with the result criterion by virtue of the continuity of at : ${\displaystyle g(x)}$ ${\displaystyle x=c}$

${\displaystyle \lim _{k\to \infty }g(a_{k})=g(c)=\lim _{k\to \infty }g(b_{k})}$.

With (i) the consequences or have an upper or lower limit, which continues to the respective limit value: ${\displaystyle (g(a_{k}))}$ ${\displaystyle (g(b_{k}))}$

${\displaystyle g(a_{k})\leq 0\Rightarrow g(c)\leq 0}$, likewise , in total thus , q. e. d. ${\displaystyle g(b_{k})\geq 0\Rightarrow g(c)\geq 0}$ ${\displaystyle g(c)=0}$

example

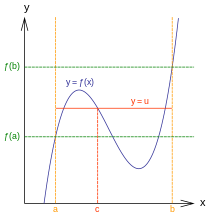
The function f takes the value u with f (a) <u <f (b) at the point c.

The cosine function is continuous in the interval , it is and . The intermediate value theorem then states that the cosine has at least one zero in the interval . In fact there is exactly one zero in the interval . ${\displaystyle \cos \left(x\right)}$ ${\displaystyle [0,2]}$ ${\displaystyle \cos \left(0\right)=1}$ ${\displaystyle \cos \left(2\right)\approx -0{,}4161<0}$ ${\displaystyle ]0,2[}$ ${\displaystyle {\tfrac {\pi }{2}}}$

generalization

The intermediate value theorem is a special case of the following theorem from topology : The image of a connected subset of a topological space with respect to a continuous mapping is again connected.

From this the intermediate value theorem can be obtained again because continuity of a function in the topological sense includes that required in the intermediate value theorem for real functions, and because a subset of the real numbers is connected if and only if it is an interval. Unlike here in the "Proof" section, the observed interval need not be restricted in this structure.

Intermediate value theorem for derivatives (Darboux theorem)

A statement analogous to the above intermediate value theorem applies to derivative functions :

If there is a differentiable function defined on the interval with , the derivative function assumes every value between and . ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ ${\displaystyle [a,b]\subseteq \mathbb {R} }$ ${\displaystyle f'(a)\neq f'(b)}$ ${\displaystyle f'}$ ${\displaystyle f'(a)}$ ${\displaystyle f'(b)}$

Note that this also applies if the derivative function is not continuous. The theorem follows from the mean value theorem of differential calculus .

Web links

Wikibooks: Math for Non-Freaks: Intermediate  Value Theorem - Learning and teaching materials

literature

• GM spruce : Calculus I . 8th edition. German Science Publishing House , Berlin 1973.
• Günter Köhler: Analysis . Heldermann Verlag , Lemgo (ua) 2006, ISBN 3-88538-114-1 .
• Konrad Königsberger : Analysis 1 . Springer, Berlin 2004, ISBN 3-540-41282-4
• Otto Forster : Analysis 1. Differential and integral calculus of a variable. Vieweg-Verlag, 8th edition 2006, ISBN 3-528-67224-2

Individual evidence

1. ↑ The train of thought corresponds to a complete induction .
2. ↑ More on the convergence of geometric sequences here .
3. ↑ because of the convergence of the boundary consequences of an interval nesting
4. ↑ cf. Statement on the limit value of a bounded convergent sequence
5. ↑ spruce wood, p. 206
6. ↑ Köhler, p. 196