Bisection
The bisection , also called continued bisection or interval halving method , is a method of mathematics and computer science . Bisection creates a finite number of links in an interval nesting , i.e. a sequence of intervals that defines exactly one real number. One interval arises from the previous one by dividing it into two halves; this is represented by the Latin components bi ("two") and sectio ("cut") of the word "bisection".
In principle, bisection processes are always used when a problem can be solved by breaking it down into two sub-problems of roughly equal size, which can then be dealt with individually.
example
A simple example is the following task: We are looking for a number between 1 and 1000 that a player should guess. He always only receives “larger” or “smaller” or “hit” as a hint.
Assuming the number is 512. If the player uses the bisection method of the binary search for guessing, the following dialog results:
- 500 - bigger
- 750 - smaller
- 625 - smaller
- 562 - smaller
- 531 - smaller
- 515 - smaller
- 507 - bigger
- 511 - larger
- 513 - smaller
- 512 - hits
If the player had searched linearly instead and started at 1, the dialogue would have taken the following course:
- 1. 1 - bigger
- 2. 2 - bigger
- ...
- 511.511 - bigger
- 512. 512 - hits
Instead of ten questions, he would have needed 512 questions; the bisection is therefore much more efficient here.
Term and Convergence
Discreet case
In the discrete case, i.e. if the underlying problem only has a finite number of solutions to be tested, such a problem can always be viewed as a search: an element with the property is to be found from a finite set . should have a function here
be, and should be considered accurate if the desired property is satisfied, that is . To solve this problem using bisection, the following should still apply:
- if
- if
The function not only indicates the hit (at ), but in the other case also indicates the direction in which the search must continue. It is of course implicitly assumed that a relation <is used to order .
is divided into two halves of the same size as possible, by first evaluating for an element as close as possible to the middle of . The case that due to an uneven number of elements can only be divided into two parts that are only approximately equal in size can be omitted, it has almost no effect with large numbers of elements. After each step, half of the last examined amount can be discarded, the amount halves with each evaluation of . The process ends at the latest when the set contains only one element; this must be the one searched for, if it was included in the initial set at all. So in order to reduce a lot of the size to 1 by continuously halving it, steps are necessary with:
Thus, the method has a running time of O .
Continuous fall
In the continuous case, the solution is usually an interval that is a sub-interval of another given finite interval. An important application is to find a small interval that contains a root of a given function:
We are looking for the zero of a continuous, strictly monotonically increasing function in the interval . This should be specified with an accuracy ; a subinterval of is searched for that contains the zero and has a maximum length of . Since there are an infinite number of such intervals, they cannot simply be tried out all. However, the following applies:
- A steady, strictly monotonically increasing function has a zero in an interval if and only if and is.
This leads to the following algorithm:
- Put and .
- Test if it contains a zero. If not: abort.
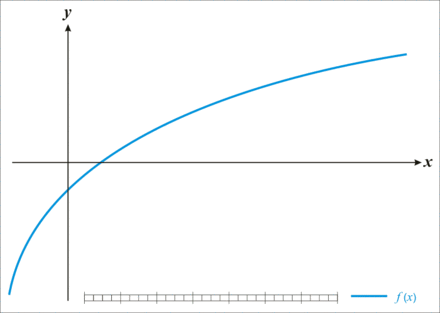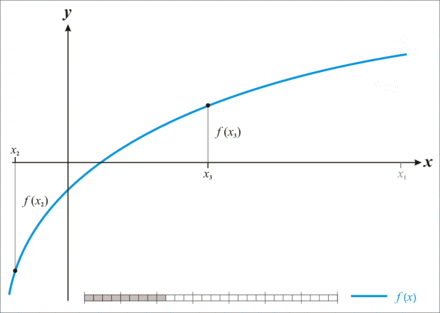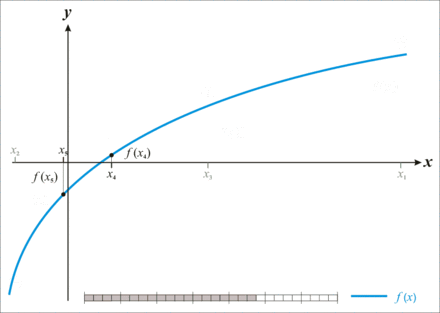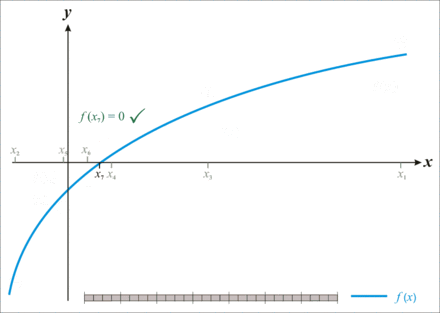
- Test if is. If so, the solution interval has been found.
- Otherwise divide in the middle and continue the process recursively from 2 with both partial intervals.
Similar to the discrete case, the algorithm ends at the latest when the interval falls below the length . So:
This results in a logarithmic run time depending on the ratio of the interval length to the desired accuracy.
The monotony of the function is not absolutely necessary. A continuous function already has at least one zero in the interval after the intermediate value theorem if . The algorithm is very similar to the one above and then looks like this:
- Put and .
- Test if . If not: abort.
- Set .
- If set else set
- Test if is. If so, the solution interval has been found.
Advantages and disadvantages of the procedure
The bisection is suitable for the following cases:
- There is a sign change in the given interval and the function is continuous
- The starting values of the classical methods ( Newton method , Regula falsi ) are not sufficiently close enough to the zero point so that no local convergence occurs there
- Multiple zeros reduce the speed of convergence of the classic methods
Disadvantages of bisection:
- In simple cases (strictly monotonic function) it is slower than a quadratically convergent method
- If there is no sign change in the given interval, additional tests are necessary to distinguish a local minimum from a zero
Bisection and binary trees
There is a close connection between bisection and binary trees . During a bisection, a decision is made in each step whether to continue with the left or right subset, and when traversing a binary tree from the root it must be decided in each node whether the left or right edge is to be followed. For a given quantity and a bisection process, there is exactly one assigned binary tree that describes all potential courses of the bisection. The tree has just as many leaves as the given problem can produce possible results. Since with every decision in a node the number of possible results is halved, he has approximately
Levels. This corresponds to the runtime of the bisection, since the number of levels determines the path length from top to bottom, which in turn is equal to the runtime. The tree resulting from this assignment corresponds to a balanced binary search tree .
Bisection and binary numbers
Bisection can also be used, for example, to determine the binary representation of a number. A number between and can be identified by a sequence of “greater than or equal to” and “less than” decisions. If a power of 2 is chosen, the element "right of the middle" can always be tapped, since the quantity is even. For example, there is the amount - the search for the 2 would now run as follows:
- 4 - smaller
- 2 - greater than or equal to (no "hit" is used)
- 3 - smaller
This describes the 2 exactly. If we now set 0 for “smaller” and 1 for “greater than or equal to”, the result is 010. This is precisely the binary representation of 2 .
















![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\ displaystyle [l, r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be45874f852a2b7bfa2df52888aaec6919238623)















