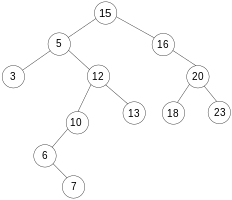
Binary tree
Binary trees are the most common subspecies of trees in computer science . In contrast to other types of trees, the nodes of a binary tree can only have at most two direct descendants.
It is usually required that the child nodes can be clearly divided into left and right child. An illustrative example of such a binary tree is the pedigree , in which, however, the parents have to be modeled by the child nodes.
A binary tree is either empty or it consists of a root with a left and right subtree, which in turn are binary trees. If a subtree is empty, the corresponding child node is called missing.
Most of the time the root is placed at the top and the leaves at the bottom in graphical representations (like the one on the right) . Correspondingly, a path from the root towards the leaf is one from top to bottom.
Terms
The terms node and edge are taken from the graphs. The edge is directed by definition (also: bow or arrow ). If it is clear enough from the context, we will only speak of an edge.
In the case of directed graphs , a node can be assigned both an output degree and an input degree. Binary trees are usually viewed as out-trees . In such a rooted tree there is exactly one node with the degree of entry 0. It is called the root . All other nodes have the entry level 1. The exit level is the number of child nodes and is limited to a maximum of two in the binary tree. Its order as an out-tree is therefore ≤ 2 .
Nodes with degree ≥ 1 are called inner nodes , those with degree 0 are called leaves or outer nodes . In the case of binary trees - and only there - the term half-leaf is occasionally used for a node with degree 1 (sometimes English: non-branching node ). Then a leaf is a double half leaf.
A binary tree is called ordered if every inner node has a left and possibly also a right child (and not just a right child), and the left node is “smaller” and the right node is “larger” than the node under consideration. It is called full if every node is either a leaf (i.e. has no child) or has two children (i.e. both a left and a right) - i.e. there is no half-leaf . The terms saturated or strict are occasionally used for the property full . Full binary trees are said to be complete when all leaves are the same depth , where the depth of a node is defined as the number of arcs to the root.
The height of a rooted tree is the maximum occurring depth. However, many authors set it one higher because the empty tree can be given the height 0 and the tree consisting only of the root can be given the height 1, which allows certain recursive definitions to be shortened. (And since depth is an attribute of a knot, but height is an attribute of the whole tree, there need not necessarily be any confusion.)
- Please note
In this article, the latter view is maintained :
- All nodes including the root and leaves carry information ("node-oriented storage").
- The height of the tree is the maximum number of node levels.
The binary tree is called degenerate when each node is either a leaf (number of children is 0) or a half-leaf (number of children is 1). In this case the tree represents a list. Special forms are the ordered lists, in which a tree consists only of left or right children.
properties
- Just as a tree with knots has edges , a binary tree with knots has edges.
- A binary tree with nodes has (immediate) insertion points .
- A binary tree with leaves and half leaves has one insertion point on each half leaf and two (immediate) insertion points on each leaf .
- If the number of inner nodes is then calculated .
Combinatorics
The number of binary trees with nodes corresponds to the number of possibilities to completely enclose a string of symbols that are separated by mathematical operators for a two-digit combination , for example addition , subtraction , multiplication or division , in brackets . Each node corresponds to a two-digit link and for each node the left subtree corresponds to the left expression and the right subtree corresponds to the right expression of the link.
For example, you have to put in brackets for a string , which can be done in five different ways:
Adding redundant parentheses around a parenthesized expression or the entire expression is not allowed.
There is a binary tree with 0 nodes and every other binary tree is characterized by the combination of its left and right subtree . If these have subtrees or nodes , the entire tree has the nodes. Hence, the number of binary trees with nodes has the following recursive description and for any positive integer . It follows that the Catalan number is with an index . It applies
| Number of binary trees | |
|---|---|
| n | C n |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| 4th | 14th |
| 5 | 42 |
| 6th | 132 |
| 7th | 429 |
| 8th | 1430 |
Applications
Binary search tree
The most important application of the binary trees in practice are the binary search trees , including the AVL trees , red-black trees and splay trees . In search trees there are “keys” in each node, according to which the nodes are arranged “linearly” in the tree. The most efficient search possible is based on this order .
Partially ordered tree
A partially ordered tree T is a special tree,
- whose nodes are marked
- whose markings come from an ordered range of values
- in which the following applies for every subtree U with the root x : All nodes from U are marked greater than x or equal to x .
Intuitively, this means: The root of each subtree represents a minimum for this subtree. The values of the subtree increase in the direction of the leaves or remain the same.
Such trees are often used in heaps .
Full binary tree and fully balanced binary tree
A full binary tree is a full binary tree (all nodes have either 2 or 0 children) in which all leaves have the same depth. Inductively, it can be shown that a complete binary tree of height , which is often referred to as being accurate
- Node,
- inner nodes (not leaf, but possibly root),
- Knots in depth for , especially so
- leaves
owns.
A fully balanced binary tree is a full binary tree in which the distances from the root to any two leaves differ by no more than 1. A complete binary tree is a fully balanced binary tree. (Compare balanced tree and AVL tree .)
More binary trees
A representation of a binary tree in which the nodes are represented by right triangles and the arcs by rectangles is called a Pythagorean binary tree .
Even Fibonacci trees and binary heaps are based on binary trees.
Representation and Access
The figure shows an obvious type of storage. It roughly corresponds to the C structures:
struct knoten { // 1 Objekt = 1 Knoten
char schlüssel;
struct knoten * links; // linkes Kind
struct knoten * rechts; // rechtes Kind
} object;
struct knoten * anker; // Zeiger auf die Wurzel
To better differentiate between the objects, they are given the keys "F", "G", "J" and "P". These keys are also used as reference targets for simplicity (instead of real memory addresses ). As usual, a pointer value 0 should express that no object is referenced, i.e. that there is no child at this point.
The big advantage of the tree compared to the array lies in the more flexible memory management: With the creation or disappearance of an object, the memory that represents it can also arise or disappear, whereas the individual entries in the array are permanently connected to it.
In-order index
If the number of elements of the associated subtree is kept in each node, the search for an element using its in-order index can be done in a very similar way to the search with a key in the binary search tree . However, this has the disadvantageous implication that insert and delete operations always require corrections right up to the root, which then also changes the in-order indices of nodes. The procedure should therefore be of questionable value with non-static binary trees, and with static binary trees the ordinary array index is superior in terms of runtime.
The effort is where is the height of the tree.
Left / right index
Each node can be precisely specified by a variable length chain of binary digits. The requirement could be as follows:
- A "0" at the beginning (at the same time the end) corresponds to the empty binary tree.
- A "1" at the beginning allows access to the root.
- A subsequent “0” or “1” allows access to the left or right child.
A binary chain can thus be clearly assigned to each node in a binary tree.
In the case of height- balanced trees, the length of the binary string is limited by, so that it can fit into an unsigned integer . A conceivable coding of the variable length in a word of fixed length allows the binary chain to begin after the first "1".
The maximum effort for an access is .
Representation by an array
A binary tree can be represented by an array , the length of which essentially corresponds to the number of nodes in the tree, more precisely: with than the height of the tree. An arrangement can be found in the binary search in the array .
Another type of representation starts with indexing at 1 with reference to the root. Then it continues “line by line”: all nodes of the same depth are numbered consecutively from left to right. That means: reading out the array from the left corresponds to a level-order-traversal (or breadth-first-traversal) of the tree. If the binary tree is not fully occupied, omitted nodes must be filled with placeholders, so that memory cells are wasted.
This numbering has the pleasant property that one can easily calculate the indices of the connected nodes. In the array A, let A i be a node, then A 2 i is its left child and A 2 i +1 its right child; the rounded half refers to parent A j .
In genealogy , this indexing scheme is also known as Kekule numbering .
Since no explicit pointers to children or parent nodes are required when mapping a binary tree into an array, this data structure is also referred to as an implicit data structure.
One application of this representation is the binary heap , which is used for sorting items.
Traversal
Traversing refers to the systematic examination of the nodes of the tree in a certain order.
There are several ways to iterate through the nodes of binary trees. A distinction is made between the following variants: (Here, "traversing the subtrees" l and r is to be understood as a recursive call.)
-
depth-first ( depth-first search ):
-
pre-order or main order ( N – l – r ):
First the root N is considered and then the left l , and finally the right subtree r . -
post-order or secondary order ( l – r – N ):
First the left l , then the right subtree r is traversed and finally the root N is considered. -
in-order or symmetrical order ( l – N – r ):
First the left subtree l is traversed, then the root N is considered and finally the right subtree r is traversed. This order corresponds to the order of the keys in binary search trees and is the given for most applications. -
reverse in-order or anti-symmetrical order ( r – N – l ):
First the right subtree r is traversed, then the root N is considered and finally the left subtree l is traversed.
-
pre-order or main order ( N – l – r ):
-
breadth-first ( breadth-first search ) or level-order :
starting at the tree root, the levels are traversed from left to right.
Recursive implementations
The action to be carried out at a node is done in the subroutine callbackthat is to be supplied by the user. A certain communication with the calling program can be done via the variable if necessary param.
preOrder( knoten, callback, param) {
// Führe die gewünschten Aktionen am Knoten aus:
callback( knoten, param );
if ( knoten.links ≠ null )
preOrder( knoten.links ); // rekursiver Aufruf
if ( knoten.rechts ≠ null )
preOrder( knoten.rechts ); // rekursiver Aufruf
}
postOrder( knoten, callback, param) {
if ( knoten.links ≠ null )
postOrder( knoten.links ); // rekursiver Aufruf
if ( knoten.rechts ≠ null )
postOrder( knoten.rechts ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( knoten, param );
}
inOrder( knoten, callback, param) {
if ( knoten.links ≠ null )
inOrder( knoten.links ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( knoten, param );
if ( knoten.rechts ≠ null )
inOrder( knoten.rechts ); // rekursiver Aufruf
}
revOrder( knoten, callback, param) {
if ( knoten.rechts ≠ null )
revOrder( knoten.rechts ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( knoten, param );
if ( knoten.links ≠ null )
revOrder( knoten.links ); // rekursiver Aufruf
}
A traversal over the whole tree includes exactly one call of one of the recursive traversal functions per node. The effort (for the pure traversal) at nodes is therefore in .
Iterative implementation
An iterative implementation allows a single crossing step, an "iteration", to be carried out from one node to its neighboring node. In the usual way, you can set up a program loop for an interval with a start and an end, search for the nodes in question one after the other and program the desired actions for them.
As an example, only the in-order traversal is shown here, which plays a major role in binary search trees in particular , since this order corresponds to the sorting order.
inOrderNext( knoten, richtung ) {
// richtung = 1 (Rechts = aufwärts = „in-order“)
// oder = 0 (Links = abwärts = „reverse in-order“)
knotenY = knoten.kind[richtung]; // 1 Schritt in die gegebene Richtung
if ( knotenY ≠ null ) {
richtung = 1 - richtung; // spiegele Links <-> Rechts
// Abstieg zu den Blättern über Kinder in der gespiegelten Richtung:
knotenZ = knotenY.kind[richtung];
while ( knotenZ ≠ null ) {
knotenY = knotenZ;
knotenZ = knotenY.kind[richtung];
}
return knotenY; // Blatt oder Halbblatt
}
// Aufstieg zur Wurzel über Vorfahren der gegebenen Richtung:
knotenY = knoten;
do {
knotenZ = knotenY;
knotenY = knotenZ.elter;
if ( knotenY = null )
return null; // knotenZ ist die Wurzel:
// d. h. es gibt kein Element mehr in dieser Richtung
} until ( knotenZ ≠ knotenY.kind[richtung] );
// knotenY ist der erste Vorfahr in der gespiegelten Richtung
return knotenY;
}
A traversal over the whole tree includes one descent (in the direction of the arch) and one ascent (in the opposite direction) per arch. A tree with knots has arcs, so that an overall traversal goes over steps. The effort for a single traverse is on average in and in the worst case in with than the height of the tree.
Descent to the first or last element
Searching for the first or last element works very much like a single traversal .
firstLast( binärBaum, richtung ) {
// richtung = Links (erstes) oder Rechts (letztes)
knotenY = binärBaum.wurzel;
if ( knotenY = null )
return null; // der Baum ist leer
// Abstieg zu den (Halb-)Blättern
do {
knotenZ = knotenY;
knotenY = knotenZ.kind[richtung];
} while ( knotenY ≠ null );
return knotenZ; // Blatt oder Halbblatt
The effort is where the height of the tree is.
Insert, insertion point
It is assumed that the navigation to an insertion point has already taken place. Insertion point means a node and a direction (right or left). An immediate insertion point in a binary tree is always a right (or left) half-leaf, an indirect one is the immediate neighbor in the specified direction and, together with the opposite direction, specifies the same place in the binary tree - for real insertion, however, the insert function must go up to Descend the half sheet, which is the immediate insertion point.
To insert, let the child refer to the new element in the required direction of the node, so that it is inserted correctly. The complexity of the insert operation is thus constant.
Once inserted, the new element is a leaf of the binary tree.
In the following example, a node with the key J is inserted into a binary tree at the (immediate) insertion point ( M , left) - the indirect one would be ( G , right).
S S / \ / \ / \ / \ G W G W / \ / \ / \ ----> / \ D M D M / \ \ / \ / \ B F P B F J P
Repeated insertion in the same place can lead to the tree degenerating into a linear list.
Clear
When deleting you have to distinguish significantly more cases. It is important e.g. B. How many children the knot has.
Case A: The node to be deleted has at most one child.
If the node is a leaf (node without children), the node is simply removed when deleting. If the node to be deleted has exactly one child, this is placed in the place of the node to be deleted.
Case B: The node to be deleted has two children.
In this case, the deletion can be carried out using both the left and the right subtree. In order to maintain the in-order sequence, however, a descent to a half-sheet is inevitable.
One possibility is to set the left subtree to the position where the node to be deleted was and to append the right subtree to the left in its rightmost position, as the example shows ( G is to be deleted):
S S
/ \ / \
/ \ / \
G W D W
/ \ / \
/ \ ----> / \
D M B F
/ \ / \ \
B F J P M
\ / \
K J P
\
K
The changes in the heights are, however, smaller if the node to be deleted is replaced by a (immediate) neighbor in the in-order sequence. In the example, F is the left neighbor of G , so it is on the far right in the left subtree; J is the right neighbor of G , so it is on the far left in the right subtree. The order in-order is F - G - J . The left / right neighbor can have a left / right subtree that has to be attached to the place where the neighbor was.
In the following example, node G to be deleted is replaced by its right neighbor J :
S S
/ \ / \
/ \ / \
G W J W
/ \ / \
/ \ / \
D M ----> D M
/ \ / \ / \ / \
B F J P B F K P
\
K
In order to give the tree as little opportunity as possible to become one-sided, you can systematically alternate between left and right descent. If balance values are available, it makes sense to prefer the descent on the possibly higher side.
Repeated deletion can lead to the tree degenerating into a linear list.
Because of the inevitable descents to the half-leaves, the complexity of the delete operation is at its worst , where the height of the tree is. Since the descent corresponds to a single traversal and the descents in a total traversal are as frequent as the ascents, the mean value of the levels to be descended converges exactly to 1 for the increasing number of nodes.
The illustrations and pseudocode show the removal of an element that has two children and a close grandson from a binary tree.
- Pseudocode
remove( binärBaum, knoten ) {
// Es sei angenommen, dass knoten.links ≠ null, knoten.rechts ≠ null
// und knoten.rechts.links ≠ null
knotenY = knoten.rechts;
while ( knotenY ≠ null ) {
knotenZ = knotenY;
knotenY = knotenZ.links;
}
// knotenZ ist der rechte Nachbar von knoten
if ( knotenZ.rechts ≠ null )
knotenZ.rechts.elter = knotenZ.elter;
knotenZ.elter.links = knotenZ.rechts;
knotenZ.rechts = knoten.rechts;
knoten.rechts.elter = knotenZ;
knotenZ.links = knoten.links;
knoten.links.elter = knotenZ; // knoten.links ≠ null
if ( knoten.elter.links = knoten )
knoten.elter.links = knotenZ;
else
knoten.elter.rechts = knotenZ;
knotenZ.elter = knoten.elter;
}
rotation
With a rotation (вращение ( Russian for rotation ) in Adelson-Velsky and Landis) one can transfer one binary tree to another and thus properties, in particular heights of subtrees (for example in red-black trees and AVL trees ) or search depths of Influence nodes (for example in splay trees ). Since all nodes involved only move “vertically” during a rotation, the in-order sequence does not change, so that the tree remains equivalent with regard to this sequence (which is the sorting sequence in search trees).
A rotation can be specified by the direction of rotation left or right and by the root of the relevant subtree. Instead of the two also a child node can be specified, in this application than the pivot ( pivot point hereinafter) of rotation. The direction of rotation is opposite to that of the child. For example, RotateLeft ( L ) causes node L to be lowered and its right child node to be raised (here as Pivot: R ). However, it is not a continuous rotation, rather a bistable rocker, i.e. the tilting of an edge (here: L ↘ R ) in its other orientation ( L ↙ R ). The requirements
- Reversal of the orientation of a directed edge
- Maintaining the in-order order
- smallest possible change in the tree
cause certain adjustments to the neighboring nodes, namely: (below) the hanging of the child between the two nodes (here: m ) as the inner child at the lower node and (above) the replacement of the previous child with the (grand) parent ( here: P ) through the top knot.
P P
/ /
L RotateLeft(L) R
/ \ --------> / \
l \ <-------- / r
R RotateRight(R) L
/ \ / \
m r l m
- Declaration on RotateLeft ( L )
L becomes R's left child . The original left child tree m of R (the sub-tree in the middle) is the right child tree of L .
- RotateRight ( R ) statement
R becomes L's right child . The original right child tree m of L is to the left child tree R .
complexity
In both cases, the new tree's suspension also changes from above. The suspensions of the outer child trees l and r are retained.
So 3 links have to be adapted, which are shown in the graphics. As a result, a rotation requires a constant running time .
Double rotation
A double rotation consists of two counter-rotating (single) rotations carried out immediately one behind the other. A node is raised by two levels. It is required , for example, when rebalancing AVL trees . The number of links to be adjusted is 5.
Triple rotations can also occur when splitting an AVL tree.
Rotation metric
The rotation distance between 2 binary trees with the same number of nodes is the minimum number of rotations required to transform the first tree into the second. With this metric, the set of binary trees with nodes becomes a metric space , because the metric fulfills definiteness, symmetry and triangular inequality . The space is a contiguous metric space with a diameter . That means: For 2 different binary trees and there is a natural number and binary trees , so that with and for each results from a rotation.
It is unclear whether there is a polynomial algorithm for calculating the rotational distance.
Convert one shape of a binary tree to another
The following conversions do not change the in-order order. Furthermore, let the number of nodes in the tree be.
- A binary tree can be converted into an ordered list with an investment of space and time.
- Since entering a single entry in an ordered list means constant effort, linear effort is easy to create given the complexity of #traversing . It is more difficult to accomplish the entry in-place , i.e. to take the space for the list pointers from the space for the binary tree.
- An ordered list can be converted into a fully balanced binary tree with expenditure of time .
- The shape of a fully balanced binary tree depends only on its number of nodes. If a subtree is to be built with a seamless sequence of nodes, then a seamless sequence of nodes is assigned to the left child tree and one of nodes to the right . This means that the distances between any two leaves from the root deviate from each other by at most 1, as must be.
- In a binary tree, each node can be given the number of nodes in its subtree with the time expenditure .
- When traversing, the number of nodes per subtree can be formed and saved in the node.
- An AVL tree can be colored as a red-black tree without changing its shape .
- The set of AVL trees is a real subset of the set of red-black trees. The evidence there shows, by the way, that you can use the heights that you write down exactly during the in-order run to make the red-black coloring.
See also
literature
- Donald Knuth : The art of computer programming vol 1. Fundamental Algorithms . 3. Edition. Addison-Wesley, 1997, ISBN 0-201-89683-4 , section 2.3, p. 318 ff.
- Horst Wettstein: System programming . 2nd Edition. Carl Hanser Verlag, 1980, ISBN 3-446-13217-1 .
- Lennart Krothaus: The binary tree - a computer science miracle . 3. Edition. MethiVerlag, 1998.
- Robert Sedgewick , Kevin Wayne: Algorithms Fourth Edition. (PDF) Pearson Education, 2011, ISBN 978-0-321-57351-3 .
Web links
- Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees . (PDF; 1675 kB) 2004 (English).
Individual evidence
- ↑ In terms of amount, the height has the same value as Knuth , who in addition to the node carrying the key (called "inner") also knows "outer" nodes , which can be understood as insertion points and which change the height (according to the first definition) Increase 1.
- ↑ The terms can be found, for example, in Knuth .
-
↑ S. a. Pfaff 2004 , p.58 “4.9.3.7 Advancing to the Next Node” with a stack memory , called “Traverser”, for the way back to the root. The solution presented requires a pointer
elterto the parent node. - ↑ Since there cannot be another node between the two nodes, the in-order sequence is not changed. This approach was proposed for the first time in 1962 by T. Hibbard (quoted from #Sedgewick p. 410.)
- ↑ GM Adelson-Velsky , EM Landis : Один алгоритм организации информации . In: Doklady Akademii Nauk SSSR . 146, 1962, pp. 263-266. (Russian)
- ↑ The uniqueness of these adjustments is (only) given for the binary trees. Because if an edge L → R is tilted, must the previously lower nodes R for the new child a "valence" L be freed. The only one in the correct direction is the valence for m . At L a valence (which previously pointed to R ) becomes free, which has the direction of m and m must take over. It is very similar at the top of the edge.
- ^ Daniel D. Sleator, Robert E. Tarjan, William P. Thurston: Rotation distance, triangulations, and hyperbolic geometry. In: Journal of the American Mathematical Society , 1, (3), 1988, pp. 647-681.