Catalan number

The Catalan numbers count, for example, the non-crossing partitions of a set with n elements, here C ₅ = 42 (above), whereby all partitions are given by Bell's numbers, here B ₅ = 52.

The Catalan numbers or Catalan numbers form a sequence of natural numbers that appear in many problems of combinatorics and play a role similar to that of the binomial coefficients or the Fibonacci numbers . They are named after the Belgian mathematician Eugène Charles Catalan .

The sequence of Catalan numbers begins with ${\displaystyle C_{0},C_{1},C_{2},C_{3},\dotsc }$

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, ... (sequence A000108 in OEIS )

The Catalan numbers are given for by ${\displaystyle n\geq 0}$

${\displaystyle C_{n}={\frac {1}{n+1}}{\binom {2n}{n}}={\frac {(2n)!}{(n+1)!\,n!}},}$

where is the mean binomial coefficient . With one gets that the formula is equivalent to ${\displaystyle {\tbinom {2n}{n}}}$ ${\displaystyle {\tbinom {2n}{n+1}}={\tfrac {n}{n+1}}{\tbinom {2n}{n}}}$

${\displaystyle C_{n}={\binom {2n}{n}}-{\binom {2n}{n+1}}}$

and thus actually only delivers whole numbers.

Historical

The Chinese Minggatu was the first to find Catalan numbers in his work on infinite series for trigonometric functions (circulated as a manuscript in the 1730s, but not published as a book until 1839).

The numbers in this series were already described in 1751 by Leonhard Euler in a letter to Christian Goldbach . In 1758 Johann Andreas von Segner found a recursion formula to which Euler gave the solution in the summary of Segner's article. A more general counting problem posed by Johann Friedrich Pfaff was solved by Nikolaus Fuss in 1795 . Gabriel Lamé , Olinde Rodrigues , Jacques Binet and Eugène Catalan took up the question again in 1838 and 1839 . In his textbook on combinatorics published in 1901, Eugen Netto traced the numbers back to Catalan.

properties

Euler was looking for the number of possibilities of dividing a convex n -gon into triangles by diagonals ( triangulation ). This number is . For example, for a pentagon there are five possible triangulations: ${\displaystyle C_{n-2}}$

Euler gave the explicit formula in his letter to Goldbach in 1751 (see history )

${\displaystyle C_{n}={\frac {2\cdot 6\cdot 10\dotsb (4n-2)}{2\cdot 3\cdot 4\dotsb (n+1)}}=\prod _{k=1}^{n}{\frac {4k-2}{k+1}}}$

(*)

and the formula

${\displaystyle \sum _{n=0}^{\infty }C_{n}x^{n}={\frac {1-{\sqrt {1-4x}}}{2x}}={\frac {2}{1+{\sqrt {1-4x}}}}}$

for the generating function , in particular

${\displaystyle \sum _{n=0}^{\infty }{\frac {C_{n}}{4^{n}}}=2}$

also as a description of growth behavior.

With the gamma function : ${\displaystyle \Gamma }$

${\displaystyle C_{n}={\frac {4^{n}\Gamma {\left({\tfrac {1}{2}}+n\right)}}{{\sqrt {\pi }}\Gamma {\left(2+n\right)}}}}$

It follows directly from the formula (*)

${\displaystyle C_{n+1}={\frac {4n+2}{n+2}}\,C_{n}.}$

The recursion formula also applies ( Segner 1758)

${\displaystyle C_{n+1}=\sum _{k=0}^{n}C_{k}\,C_{n-k},}$

for example is . ${\displaystyle C_{3}=C_{0}\,C_{2}+C_{1}\,C_{1}+C_{2}\,C_{0}}$

Another recursion formula is

${\displaystyle C_{n+1}=\sum _{k=0}^{\lfloor n/2\rfloor }{\binom {n}{2k}}2^{n-2k}\,C_{k}.}$

as well as with the Motzkin numbers M (sequence A001006 in OEIS )

${\displaystyle C_{n+1}=\sum _{k=0}^{n}{\binom {n}{k}}\,M_{k}.}$

Since all prime factors of , see formula (*), are less than and for , and are the only Catalan numbers also prime numbers . The formula also shows that every prime number between and is divisible exactly once and is odd if and only if it is a power of 2. ${\displaystyle \textstyle C_{n}=2^{n}\,{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{2\cdot 3\cdot 4\cdots (n+1)}}}$ ${\displaystyle 2n}$ ${\displaystyle C_{n}>2n}$ ${\displaystyle n>3}$ ${\displaystyle C_{2}=2}$ ${\displaystyle C_{3}=5}$ ${\displaystyle C_{n}}$ ${\displaystyle n+1}$ ${\displaystyle 2n}$ ${\displaystyle n+1}$

From the set of Wolstenholme following congruence

${\displaystyle (p\,n+1)\,C_{p\,n}\equiv (n+1)\,C_{n}\ ({\text{mod }}p^{3})}$

for every prime number , for Wolstenholme prime numbers, the congruence (mod p ⁴ ) applies, for the prime numbers 2 and 3 it applies (mod p ² ). ${\displaystyle p>3}$

In particular, is and for every prime and integer . ${\displaystyle C_{p^{k}n}\equiv (n+1)\,C_{n}\ ({\text{mod }}p)}$ ${\displaystyle C_{p^{k}}\equiv 2\ ({\text{mod }}p)}$ ${\displaystyle p}$ ${\displaystyle k>0}$

By inserting the Stirling formula one gets for the asymptotic behavior of the Catalan numbers

Error when parsing (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") From server "/ mathoid / local / v1 /" :): {\ displaystyle C_n \ sim 4 ^ n / \ bigl ((n + 1) \ sqrt {\ pi n} \, \ bigr).}

The sum of the reciprocal values ​​converges:

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{C_{n}}}=2+{\frac {4{\sqrt {3}}\pi }{27}}}$

In addition, the following applies (consequence A013709 in OEIS 2016):

${\displaystyle \sum _{n=0}^{\infty }\left({\frac {C_{n}}{2^{2n+1}}}\right)^{2}(n+1)={\frac {1}{\pi }}}$ such as

${\displaystyle \sum _{n=0}^{\infty }\left({\frac {C_{n}}{2^{2n+1}}}\right)^{2}(4n+3)=1}$

${\displaystyle \sum _{n=0}^{\infty }\left({\frac {C_{n}}{2^{2n}}}\right)^{2}(n+1)={\frac {4}{\pi }}=\sum _{n=-1}^{\infty }\left({\frac {C_{n}}{2^{2n+1}}}\right)^{2}}$ (Wallis-Lambert series) with ${\displaystyle C_{-1}=-{\frac {1}{2}}}$

Using the Cauchy product formula with the Basel problem results from this (sequence A281070 in OEIS 2017):

${\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{n}\left({\frac {C_{k}}{2^{2k+1}}}\right)^{2}{\frac {k+1}{(n-k+1)^{2}}}={\frac {\pi }{6}}}$

Further interpretations

The Catalan numbers appear in numerous enumeration problems, which are graph-theoretical enumerations of trees . So is the number of ${\displaystyle C_{n}}$

• Bracketing of a product in which n multiplications occur, or, equivalent, with n +1 factors, so that only the multiplication of two factors has to be carried out (Catalan 1838). For example, is because all possible brackets are and . ${\displaystyle C_{3}=5}$ ${\displaystyle x_{1}x_{2}x_{3}x_{4}}$ ${\displaystyle (x_{1}x_{2})(x_{3}x_{4}),\ (x_{1}(x_{2}x_{3}))x_{4},\ x_{1}((x_{2}x_{3})x_{4}),\ ((x_{1}x_{2})x_{3})x_{4}}$ ${\displaystyle x_{1}(x_{2}(x_{3}x_{4}))}$

This is, for example, a measure of the number of possible calculation sequences in non-commutative matrix chain multiplication , where the computational effort can be minimized through cleverly optimized brackets.

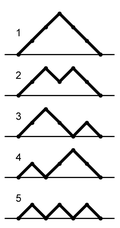
• one-dimensional random walks from 0 to 2 n with start and end point in 0, so that the path is never below the x-axis (so-called Dyck paths according to Walther von Dyck ). For example , because all possible paths are: ${\displaystyle C_{3}=5}$

• ordered full binary trees with 2 n  + 1 nodes or, equivalent, with n  + 1 leaves (= end corners). The following diagram shows one of = 1430 such binary trees for n  = 8: ${\displaystyle C_{8}}$

• possible counting processes in an election in which candidate A is never behind candidate B after each counted vote, if both candidates receive n votes each and the ballot papers are taken from the ballot box and counted one after the other. For example, for n  = 2, the possible drawing sequences that meet the requirement would be ABAB and AABB.
• Ways how 2 n people sitting at a round table can shake hands in pairs across the table without crossing their arms.

literature

• Peter J. Hilton , Jean Pedersen: Catalan numbers and paths in an integer grid. Elements of Mathematics 48, 1993, pp. 45-60.
• Jürgen Schmidthammer: Catalan numbers. ( PDF file; 7.05 MB), admission thesis for the state examination, Erlangen, February 1996.
• Thomas Koshy: Catalan Numbers with Applications. Oxford University Press, New York 2009, ISBN 978-0-19-533454-8 .
• Richard P. Stanley : Enumerative combinatorics. Volume 2, Cambridge University Press, Cambridge 1999, ISBN 0-521-56069-1 (English; Stanley's website for the book with a continuously updated list of interpretations of the Catalan numbers: Information on Enumerative Combinatorics ).

Web links

Commons : Catalan Numbers  - collection of images, videos and audio files

• Eric W. Weisstein : Catalan Number . In: MathWorld (English).
• Lattice Paths: Catalan Numbers in the NIST Digital Library of Mathematical Functions (English)

Individual evidence

1. ↑ ^{a b} Letter ( PDF file; 137 kB) from Euler to Goldbach of September 4, 1751, printed in Paul Heinrich Fuss (ed.): Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle. (Volume 1), St.-Pétersbourg 1843, J & pg = PA549 pp. 549-552.
2. ↑ ^{a b} Ioh. Andr. de Segner : Enumeratio modorum quibus figurae planae rectilineae per diagonal dividuntur in triangula . Novi commentarii academiae scientiarum imperialis petropolitanae 7 pro annis 1758 et 1759, 1761, pp. 203-210 (Latin).
3. ^ Leonhard Euler: Summarium dissertationum . Novi commentarii academiae scientiarum imperialis petropolitanae 7 pro annis 1758 et 1759, 1761, pp. 13-15 (Latin).
4. ↑ Nicolao Fuss : Solutio quaestionis, quot modis polygonum n laterum in polygona m laterum, per diagonales resolvi queat . Nova acta academiae scientiarum imperialis petropolitanae 9, 1795, pp. 243-251 (Latin).
5. ↑ Gabriel Lamé : Extrait d'une lettre de M. Lamé à M. Liouville sur cette question: Un polygone convexe étant donné, de combien de manières peut-on le partager en triangles au moyen de diagonales? Journal de mathématiques pures et appliquées 3, 1838, pp. 505-507 (French).
6. ↑ Olinde Rodrigues : Sur le nombre de manières de décomposer un polygone en triangles au moyen de diagonales and Sur le nombre de manières d'effectuer un produit de n facteurs . Journal de mathématiques pures et appliquées 3, 1838, pp. 547-549 (French).
7. ^ J. Binet : Problems on the polygones . Société philomathique de Paris - Séances de 1838 - Extraits des procès-verbaux, pp. 127–129 (French).
8. ↑ J. Binet: Réflexions sur leproblemème de déterminer le nombre de manières dont une figure rectiligne peut être partagée en triangles au moyen de ses diagonales . Journal de mathématiques pures et appliquées 4, 1839, pp. 79-90 (French).
9. ↑ ^{a b} E. Catalan : Note sur une equation aux différences finies. Journal de mathématiques pures et appliquées 3, 1838, pp. 508-516 , and 4, 1838, pp. 95-99 (French).
10. ↑ E. Catalan: Solution nouvelle de cette question: Un polygone étant donné, de combien de manières peut-on le partager en triangles au moyen de diagonales? Journal de mathématiques pures et appliquées 4, 1839, pp. 91-94 (French).
11. ^ Eugen Netto : Textbook of Combinatorics . BG Teubner, Leipzig 1901 (return of the numbers to Catalan in § 122, pp. 192–194 and § 124, p. 195).
12. ^ Whole sum of the reciprocal Catalan numbers. At: juanmarqz.wordpress.com. July 29, 2009. Retrieved February 18, 2017.
13. ↑ ^{a b} Doina Logofătu: Algorithms and problem solving with C ++. Chapter 8 Catalan Numbers. Vieweg-Verlag, 1st edition 2006, ISBN 978-3-8348-0126-5 , pp. 189-206.