Leonhard Euler
Leonhard Euler ( Latin Leonhardus Eulerus * 15. April 1707 in Basel , † September 7 . Jul / 18th September 1783 greg. In Saint Petersburg ) was a Swiss mathematician , physicist , astronomer , geographer , logician and engineering . He made important and far-reaching discoveries in many branches of mathematics, such as calculus and graph theory . At the same time, Euler made fundamental contributions in other areas such as topology and analytical number theory . He coined large parts of the mathematical terminology and notation used worldwide to this day. For example, Euler introduced the concept of mathematical function to analysis . He is also known for his work in mechanics , fluid dynamics , optics , astronomy and music theory .
Euler, who spent most of his life in Saint Petersburg and Berlin , was one of the most important mathematicians of the 18th century. His outstanding achievements were already recognized by his contemporaries and did not ebb after he went blind in 1771. Today he is considered one of the most brilliant and productive mathematicians of all time. His collected writings, Opera omnia , so far comprise 76 volumes - a mathematical work, the scope of which remains unmatched to this day.
Two mathematical constants were even named after Leonhard Euler: Euler's number (base of the natural logarithm ) and the Euler-Mascheroni constant from number theory, which is sometimes simply called Euler's constant .
Leonhard Euler's work inspired many generations of mathematicians, including Pierre-Simon Laplace , Carl Gustav Jacobi and Carl Friedrich Gauß . Laplace is said to have said to his students: "Read Euler, he is all of us master!"
biography
Childhood, youth and education
Euler was the eldest son of pastor Paul III. Euler (1670–1745) and his wife Margaretha Brucker (1677–1761), a pastor's daughter, were born in Basel. He had two younger sisters, Anna Maria and Maria Magdalena, and a younger brother, Johann Heinrich.
Soon after Leonhard's birth, the Euler family moved from Basel to the neighboring village of Riehen , where Leonhard spent most of his childhood from 1708 onwards. The spiritual climate in the parish household was inspiring: Euler's mother herself came from an educated family, and the father had mathematical interests and not only listened to lectures from Jakob I Bernoulli , but even wrote a mathematical dissertation in 1688. Leonhard Euler attended high school on Münsterplatz in Basel and at the same time received private lessons from theologian Johannes Burckhardt (1691–1743). His father had arranged this for him because math classes at the school had been canceled. It is also well established that the young Euler the book regulate nimbly and pretty bill through the artful Algebre so gemeinicklich the COSS be genennt, by Christoph Rudolff successfully studied (1499-1545). The mathematics-loving father was friends with the Bernoullis and especially Europe's leading mathematician Johann I Bernoulli , who would later have a great influence on the young Leonhard.
In 1720, at the age of 13, he enrolled at the University of Basel . At the request of his father, who had planned a pastoral career for his son, Euler began to study theology as well as the Greek and Hebrew languages. Three years later he received his master's degree . In the dissertation submitted, he compared the philosophies of Descartes and Newton . In the meantime, he had taken weekly lessons from Johann Bernoulli, who recognized and began to promote his new student's extraordinary talent for mathematics. Bernoulli then convinced Paul Euler that Leonhard should turn to mathematics and physics.
In 1726 Euler completed another dissertation entitled De Sono , a work on the propagation of sound . In 1727 he first took part in the competition for the Paris Academy Prize, in which the aim was to solve the problem of the optimal placement of ship masts. Each year the Paris Academy compiled an award report and the reports were then published in its prize books Pièces qui ont remporté le prix de l'académie royale des sciences de Paris (works that won the prize of the Royal Academy of Sciences in Paris) . Euler's submitted work only took third place, but it solved a problem. The competition was won by Pierre Bouguer , who later became known as the "father of shipbuilding". Later on, Euler was able to win the competition in a total of twelve cases. From the first call for tenders in 1720 until most of the eighteenth century, the Prix de Paris was considered the most important scientific award in Europe.
Time in Saint Petersburg
Around this time Johann Bernoulli's two sons, Daniel and Nikolaus , were working at the Imperial Russian Academy of Sciences in Saint Petersburg . On July 31, 1726, Nicholas died of appendicitis. When Daniel took over his brother's position in the mathematics / physics department, he recommended that his friend Euler fill the position he had vacated in physiology . In November 1726 Euler accepted the offer, but delayed the trip to Saint Petersburg while he unsuccessfully applied for a physics professorship at the University of Basel.
Euler arrived in Saint Petersburg on May 17, 1727. He was promoted from his junior position in the Academy's medical department to a position in the math department. During this time he lived with Daniel Bernoulli, with whom he often worked closely. After a short stay, Euler was already fluent in Russian and settled in Saint Petersburg. Some sources (primarily older secondary works) claim that he became a medic in the Russian Navy (based on a Paris Academy award for ship masts and physiology courses ) . However, there is no record of this.
The academy founded by Peter the Great in Saint Petersburg was supposed to improve education in Russia and catch up with Western Europe's scientific lead. To this end, it was made particularly attractive to foreign scientists like Euler. The academy had ample financial resources and an extensive library that came from the private libraries of Peter and the nobility. In order to relieve the faculty's teaching activities, very few students were enrolled at the academy. The academy placed increased emphasis on research and offered its members both the time and the freedom to pursue scientific questions.
Catherine I , who had continued her late husband's progressive policies and supported the Academy, died on the day of Euler's arrival. With the rise of twelve-year-old Peter II , the Russian nobility gained influence. The aristocracy, who opposed the academy's foreign academics, cut funding and caused increasing difficulties for Euler and his colleagues.
After the death of Peter II, the conditions for science improved a little. Thanks to his achievements, Euler rose quickly and was appointed professor of physics in 1731. Two years later, Daniel Bernoulli, who could no longer endure the censorship and hostilities in Saint Petersburg, traveled to Basel. Euler finally took up the professorship for mathematics as his successor in 1733.
On January 7, 1734 he married Katharina Gsell (1707–1773), a daughter of the painter Georg Gsell from his first marriage to Marie Gertrud van Loen. The young couple bought a house on the Neva . Of her 13 children, only five survived childhood. Charlotte Anna Wilhelmine (* 1773; † 1831), the granddaughter of his son Johann Albrecht (* 1734; † 1800), was married to Jakob Bernoulli (* 1759; † 1789) without children.
In Euler's own assessment, the Petersburg years had matured him into a strong scientist. This emerges from various surviving letters from his time in Berlin.
Time in Berlin
Concerned about the ongoing political turmoil and power struggles as a result of the death of Tsarina Anna I in Russia, Euler left Saint Petersburg on June 19, 1741 to take up a position at the Royal Prussian Academy of Sciences in Berlin , which Frederick II had given him . had been offered by Prussia. Euler corresponded there with Christian Goldbach and compared his theories with his own.
In addition, Euler was asked to serve as a tutor to Friederike Charlotte von Brandenburg-Schwedt , Friedrich's second cousin. In the early 1760s, Euler wrote over 200 letters to her, which were later compiled into a book entitled Letters to a German Princess on various subjects from physics and philosophy . This work contained Euler's remarks on various topics in physics and mathematics and offered valuable insights into his personality and religious beliefs. The book became more popular than any of his mathematical works and was published across Europe and the United States . The popularity of the "Letters" testifies to Euler's ability to effectively convey scientific subjects to a lay audience, something that was considered rare among dedicated researchers.

Euler's eyesight deteriorated over the course of his mathematical career. In 1738, three years after he was critically ill in the meantime (it is not possible to tell from the records of Euler's doctor at the time, which illness was present), he became almost completely blind in his right eye. However, Euler blamed the arduous work on cartography for the St. Petersburg Academy for this. His eyesight in this eye deteriorated so much during his stay in Germany that Friedrich soon referred to him as “my Cyclops ”. Euler commented on his loss of vision: “Now I will have less distraction”.

Despite Euler's immense contribution to the reputation of the academy, he got into an argument with Friedrich. The Prussian king had a large circle of intellectuals at his court. However, he found the mathematician to be uncultivated and ill-informed about things beyond numbers and values. In a letter to his brother August Wilhelm , Friedrich wrote:
“Dearest brother! I thought to myself that your conversation with Herr Euler would not edify you. His epigrams consist of calculating new curves, some conic sections or astronomical measurements. Among the scholars there are enormous calculators, commentators, translators, and compilers who are useful in the republic of science, but otherwise anything but brilliant. They are used like the Doric columns in architecture. They belong in the lower floor, as the bearer of the whole building and the Corinthian columns that form its decoration. "
As a simple, pious man who never questioned the existing social order or conventional convictions, Euler was in many ways the exact opposite of Voltaire , who enjoyed a high priority at Friedrich's court. Euler was not a skilled speaker and often made it his business to argue on subjects he knew little about, which made him a target of ridicule on the part of Voltaire. In the dispute between Pierre Maupertuis and Voltaire, called the academy dispute , Euler was one of the few on Maupertuis' side, alongside Friedrich II.
Friedrich had little understanding for Euler's way of working and expressing himself. Among other things, Euler's attempts to treat music on the basis of mathematics could only provoke malicious remarks from Friedrich. He also expressed disappointment with Euler's practical skills as an engineer :
«Je voulus faire un jet d'eau en mon Jardin; le Ciclope Euler calcula l'éffort des roues, pour faire monter l'eau dans un bassin, d'ou elle devoit retomber par des canaux, afin de jaillir à Sans-Souci. Mon Moulin a été éxécuté géométriquement, et il n'a pu élever une goutte d'eau à Cinquante pas du Bassin. Vanité des Vanités! Vanité de la géométrie. »
“I wanted to have a fountain built in my garden. The Cyclops Euler calculated the forces of the wheels through which the water should rise into a basin, fall down again, flow through canals and jump in Sanssouci . My water art was laid out mathematically, and could not raise a drop fifty paces in the air. O vanity of vanities! O vanity of geometry! "
According to the physicist Michael Eckert , the failure of the construction project is not due to Euler's calculation errors, but rather poor quality building material.
The reason for the final break between Euler and Friedrich, however, is the refusal of the monarch to appoint Euler as his successor for the office of President of the Academy after the death of Pierre Maupertuis . Instead, Frederick favored the French mathematician Jean-Baptiste le Rond d'Alembert . When the latter did not accept the post and instead suggested Euler, Friedrich ignored this. In response, Euler submitted a request for dismissal, but his request was unsuccessful. Friedrich only let him go after a second attempt. Shortly after Euler's departure, Friedrich appointed the mathematician Joseph-Louis Lagrange , with whom Euler had worked on the development of the calculus of variations , as president.
Euler lived in Berlin for a total of 25 years, where he wrote over 380 articles. In Berlin he published two of his most famous works: the Introductio in analysin infinitorum , a text on functions published in 1748 , and the work Institutiones calculi differentialis , which deals with differential calculus and was published in 1755. In 1755 he was also elected a foreign member of the Royal Swedish Academy of Sciences .
Return to Saint Petersburg and death
In 1760, when the Seven Years War was underway, Euler's court in Charlottenburg was looted by the advancing Russian troops. When General Ivan Petrovich Saltykov found out about the incident, he paid compensation to Euler for his lost property, with Empress Elizabeth of Russia later adding a further payment of 4,000 rubles - an enormous sum at the time. The political situation in Russia stabilized after the accession of Catherine the Great , so that Euler accepted an invitation to return to the St. Petersburg Academy in 1766. Euler set conditions: an annual salary of 3,000 rubles, a pension for his wife and a promise to appoint his sons to high positions. All of these requests were granted. He should spend the rest of his life in Russia.
In 1771 he became completely blind. He had developed a cataract in his left eye, which was discovered in 1766. The restoration of his vision through surgery on his left eye temporarily improved his vision. However, in October he became almost completely blind from a complication, possibly an infection, and was occasionally in pain. He was 59 years old at the time. His condition seemed to have little effect on his productivity, as he compensated for a lot with his mental arithmetic skills and his extraordinary memory. With the help of his scribes, Euler was even able to increase his publication rate. The Eulers had a double name, Euler-Schölpi, which is derived from "schelb" and "crooked" and stands for squinted or crooked eyes. This suggests that the Eulers may all have had a susceptibility to eye problems.
Despite being blind, almost half of his life's work was created in the second St. Petersburg period. He received help from his sons Johann Albrecht , Karl and Christoph and from his secretary Nikolaus Fuss . Despite his academic productivity, he never became president of the university. Euler's relationship with the director of the Petersburg Academy, Vladimir Grigoryevich Orlov , who took up the post at the age of 23, proved difficult again. Euler soon withdrew from his official academic duties at the Petersburg Academy, which gave him more freedom for his academic work.
In addition to his blindness, his second stay in Russia was also marked by other decisive events. A fire in Saint Petersburg in 1771 cost him his home and almost his life. His library and furniture, among other things, fell victim to the flames, but Vladimir Orlov's quick reaction saved many manuscripts. One loss was a work on lunar theory that should have been published by the Paris Academy in 1772. Johann Albrecht Euler then had to rewrite it word for word. In 1773 his first wife Katharina died. The loss made domestic life extremely difficult, as Katharina had run the entire household. Euler was determined to remain independent and not rely on his sons, although it was quite common at the time for an older parent to live with the children and be under their care. As in the first Saint Petersburg period, he worked in the Kunstkammer .

Three years after the death of his wife, Euler married her half-sister Salome Abigail Gsell (1723-1794), daughter of Georg Gsell and his third wife Maria Dorothea Gsell , daughter of Maria Sibylla Merian . This marriage lasted until his death. In 1782 he was elected an honorary foreign member of the American Academy of Arts and Sciences .
On September 18, 1783 (of the Gregorian calendar ) Euler discussed the newly discovered planet Uranus and its orbit after lunch with his family and colleague Anders Johan Lexell in Saint Petersburg when it collapsed as a result of a cerebral hemorrhage . A few hours later, around eleven o'clock that night, he died. Jacob von Staehlin wrote a short obituary for the Russian Academy of Sciences, and Nikolaus Fuss gave a more detailed eulogy at a memorial meeting. In view of Euler's demise, Marquis de Condorcet wrote:
"[...] he stopped calculating and living."
Euler was buried next to his wife in the Lutheran Smolensk Cemetery on Vasilyevsky Island in Saint Petersburg. The Russian Academy of Sciences put a stone on the grave in 1837 . In 1956, to commemorate the 250th anniversary of Euler's birthday, the tombstone was reburied together with his remains in the necropolis in the Lazarus cemetery of the Alexander Nevsky Monastery .
Euler's pioneering achievements in many fields were already well known to his contemporaries. He was celebrated as "Analysis incarnate" and "Sun of all mathematicians". In his detailed eulogy, Nikolas Fuss emphasized Euler's influence on science:
“These are Euler's contributions to the enlightenment of his age, this is his work worthy of immortality. His name, which posterity will associate with that of Galileo, Descartes, Leibnitz, Newton and so many other great men who have honored humanity with their genius, can only be extinguished with the sciences. [...] Few scholars have written as much as Euler, no geometer covered so many objects at once, no one shed so much light over all parts of mathematics. "
This obituary is one of the most famous that has come down from the history of science. The original version was written in French and was read on October 23, 1783 (Gregorian: November 3) in the Imperial Academy of Sciences in Saint Petersburg .
After the October Revolution of 1917, some of his descendants returned from Russia to Switzerland, including the parents of the later National Councilor Alexander Euler (1929–2012).
Scientific work
Euler's research was very diverse. He worked in almost all areas of mathematics and is considered one of the most productive mathematicians in history. Among other things, he published on geometry , calculus , trigonometry , algebra and number theory , as well as continuum mechanics , lunar theory and other areas of physics. His collected works of the Opera omnia comprise 74 volumes. A total of 866 publications by him are known. His oeuvre thus comprises an estimated one third of the entire body of mathematical, physical and mechanical research within the last three quarters of the 18th century. Euler's name is associated with a large number of results and scientific subjects.
Two mathematical constants are named after Leonhard Euler : Euler's number from analysis and the Euler-Mascheroni constant γ (gamma) from number theory, which is sometimes referred to as Euler's constant and is approximately equal to 0.57721.
His mathematical work inspired many generations of mathematicians. Among other things, he influenced the work of Pierre-Simon Laplace , Joseph-Louis Lagrange , Carl Friedrich Gauß , Carl Gustav Jacobi , Niels Henrik Abel , Évariste Galois , Karl Weierstraß and Bernhard Riemann .
Mathematical notations
Euler introduced several notation conventions in his numerous textbooks. Due to the widespread use of the books, many of his notations became firmly established. He introduced the concept of the mathematical function and was the first to write f (x) to denote the function f that is applied to the argument x . The notations for the trigonometric functions , the letter e for the base of the natural logarithm , the Greek letter Σ ( sigma ) for sums and the letter i to denote the imaginary unit also come from him . The use of the Greek letter π to denote the ratio of circumference and diameter ( circle number ) was also popularized by Euler, although it originally goes back to the Welsh mathematician William Jones .
Analysis
Euler can be seen as one of the founders of analysis . Because of continued research, calculus was on the rise in the 18th century. Euler's friends, the Bernoullis, in particular, were responsible for much of the early advances in this area. Thanks to their influence, the study of calculus became the main focus of Euler's work.
Above all, his proof of the Taylor series of the exponential function was groundbreaking
as well as his solution to the so-called Basel problem :

Euler first used the exponential function and logarithms in analytical proofs and successfully defined them for complex numbers . This greatly expanded their scope of application. This is how he found the close relationship to the trigonometric functions. For every real number (in radians ), Euler's formula says that the complex exponential function is the equation
Fulfills. A special case of the above formula is called Euler's identity
known.
Number theory
Euler's interest in number theory can be traced back to the influence of Christian Goldbach , a friend at the St. Petersburg Academy. Much of Euler's early work on number theory is based on the works of Pierre de Fermat . Euler developed some of Fermat's ideas and refuted some of his guesses.
Euler linked the nature of the prime number distribution with ideas from analysis. For example, he proved that the sum of the reciprocal values of the prime numbers diverges . In doing so he found the connection between the Riemann zeta function and the prime numbers; his discovery is known today as the Euler product formula for the Riemann zeta function. He used analytical methods to gain some understanding of the distribution of prime numbers. Euler's work in this area led to the development of the prime number theorem .
Euler proved Fermat's little theorem , Fermat's theorem about the sum of two squares , and he made important contributions to Lagrange's four-squares theorem . He also introduced Euler's Phi function . Using the properties of this function, he generalized Fermat's little theorem into what is now known as Euler's theorem. He made a major contribution to the theory of perfect numbers , which had fascinated mathematicians since Euclid . Euler proved that the relationship between (even) perfect numbers and Mersenne primes shown by Euclid is even one to one , a result known as the Euclid-Euler theorem . Euler also suspected the law of quadratic reciprocity , which was later proven by Carl Friedrich Gauß . This is one of the most basic concepts in number theory. In 1772 Euler had proven that 2,147,483,647 is a Mersenne prime number. It was considered the largest prime number found until 1867.
Various numbers and sequences of numbers are named after Euler , see Euler's numbers (disambiguation) .
Applied Mathematics
Euler's greatest successes include analytical solutions to practical problems and the description of numerous applications of Bernoulli numbers , Fourier series , Euler numbers , the constants e and π , continued fractions and integrals . He integrated Leibniz's differential calculus with the Method of Fluxions (Newton's description of the derivative ) and developed techniques that made it easier to apply mathematics to physical problems. He made great strides in improving the numerical approximation of integrals. The most notable of these approximations are the explicit Euler method and the Euler-Maclaurin formula . He recognized the usefulness of differential equations and introduced the Euler-Mascheroni constant :
the u. a. plays a role in Zipf's law , but also in numerous other fields. In other works, Euler dealt with the application of mathematical methods in the social and economic sciences (for example population growth, pension accounts , lotteries , life expectancy and life insurance ). The Euler-Lotka equation is partially named after him because of his contributions to population dynamics .
Graph theory and topology

In 1735 (published in 1736 and published in 1741) , Euler presented a solution to the Königsberg bridge problem with the work Solutio problematis ad geometriam situs pertinentis . The city of Königsberg in Prussia lay on the Pregel River and comprised two large islands that were connected to one another and to the mainland by seven bridges. The problem is deciding whether it is possible to choose a path that crosses each bridge exactly once and returns to the starting point. This is not possible because there is no Euler cycle for this graph . Euler's solution is considered to be the first theorem of graph theory , especially planar graph theory .
Euler discovered the formula for the number of vertices ( E ), edges ( K ) and surfaces ( F ) of a convex polyhedron , a planar graph. The constant in this formula is now known as the Euler characteristic of the graph (or other mathematical object) and is directly related to the mathematical gender of the object. The study and generalization of this formula, particularly by Cauchy and L'Huilier , marked the beginning of topology .
logic
Euler is credited with using closed curves to illustrate syllogistic reasoning. These diagrams have come to be known as Euler diagrams. In the letters to a German princess 101 to 108 written in February and March 1761, Euler introduced the diagrams now known as the Venn diagrams, although this is a misnomer. Diagrams for mathematical representations in logic appeared in some eighteenth-century treatises on the subject, and it is possible that Johann Heinrich Lambert used them shortly before Euler's letters. In Letters 101 and 102, Euler emphasized the need for disciplined language in the presentation of general ideas and their expansion; he used circles on diagrams to explain various forms of syllogisms and hypothetical propositions .
Physics and astronomy
Euler has made a name for himself in many classical areas of physics .
In writings such as Mechanica, sive motus scientia analytica exposita (1736) and Theoria motus corporum solidorum seu rigidorum (1765), Euler applied mathematics to questions of physics. On September 3, 1750, he read a mémoire in front of the Berlin Academy of Sciences in which he presented the principle “force equals mass times acceleration” in the context of the “Euler's equation of rigid body rotation” as a new discovery of his own.
In 1757 he published important equations describing the flow of frictionless elastic fluids. These are known today as Euler equations in fluid mechanics . In addition, Leonhard Euler worked in mechanics in the areas of turbine equation and gyro theory ( Euler's gyro equations ).
The first analytical description of the buckling of a bar loaded with a compressive force goes back to Euler; he founded the stability theory . He helped develop the Euler-Bernoulli beam equation , which became a cornerstone of engineering. Aside from successfully applying his analytical tools to problems in classical mechanics, Euler also applied them to astronomy - this work was recognized throughout his career by a number of awards from the Paris Academy. His achievements include accurately determining the orbits of comets and other celestial bodies , understanding the nature of comets, and calculating solar parallax . His calculations contributed to the development of precise longitude tables .
In optics , he published works on the wave theory of light and the calculation of optical lenses to avoid color errors . He contradicted Newton's corpuscle theory of light, which was dominant at the time, in the Opticks . His work on optics from the 1740s contributed to the wave theory of light proposed by Christiaan Huygens becoming the predominant way of thinking, at least until the development of the quantum theory of light.
In 1745 Euler translated the work New principles of gunnery by the Englishman Benjamin Robins into German, greatly expanding its scope. Thanks to Robins and Euler's help, "the first textbook on ballistics" was created. For example, it was introduced in France (in French translation) as an official textbook in military schools. Napoleon Bonaparte had to study it as a lieutenant.
Less well-known are his work on the stability criterion of ships, in which he renewed the knowledge that Archimedes had already acquired but had lost again .
Mathematical music theory
In the field of music, too, Euler's thoughts were mainly based on mathematics. Although his writings on music theory make up only a small part of his work (a few hundred pages for a total production of about thirty thousand pages), they nonetheless reflect an early interest that has not left him in his entire life. One of his priorities was the assignment of a "degree of loveliness" to multiple sounds such as musical intervals or chords such as triads. This can be understood abstractly as a number-theoretic function and implies an increased complexity (i.e. decreasing comfort) of the sound with increasing values.
Popular representations and themes
His popular scientific treatise Lettres à une princesse d'Allemagne from 1768, in which he wrote letters to Princess Friederike Charlotte von Brandenburg-Schwedt , a niece of Frederick II, learned the basics of physics and astronomy, achieved special significance among the general public , mathematics, philosophy and theology. In addition, he devoted himself to chess mathematics , for example the knight problem . He is the inventor of the Latin square , a predecessor of Sudoku .
Beliefs about philosophy and religion
Euler and his friend Daniel Bernoulli both rejected Leibniz's monadology and Christian Wolff's philosophy . Euler was convinced that knowledge (at least in part) is based on precise quantitative laws, something that monadology and Wolffian science could not achieve. Euler's religious inclinations may have influenced his aversion to this doctrine; he even went so far as to describe Wolff's ideas as " pagan and atheistic ". A religious conviction in the sense of the Reformed faith was also emphasized in his funeral oration. This makes it understandable that he and the Enlightenment Voltaire , at the same time at the Prussian court, did not find a consensus on worldview.
In a letter from August 1736 to the Danzig mathematician Karl Leonhard Gottlieb Ehler , Euler, who mostly avoided scientific disputes, began cautiously with criticism of Christian Wolff's Philosophia prima sive ontologia (1729), Cosmologia generalis (1731) and the “Theory of positive and negative infinity ”, given in the last edition of Elementa matheseos universae (1710). He did not accept the way Wolff interpreted the term when using L'Hospital's rule . Although he agreed with Leibniz and Wolff that infinitesimal quantities are "absolute zeros" (this view was a result of Euler's "zero calculation"), he was formally of the opinion that the relationship was only a fixed "finite" in special situations Number "represents. Michael Segre shows that Euler later took up this problem in his Institutiones calculi differentialis (1755) through the conclusion and thus .
Much of what is known about Euler's religious beliefs can be inferred from his letters to a German princess and an earlier work, The Salvation of Divine Revelation Against the Objections of Frey Spirits . These works show that Euler was a devout Christian who found the Bible to be a guide; The rescue was primarily an argument for the divine verbal inspiration . Euler was active in the Reformed church.
There is a famous anecdote , inspired by Euler's debates with secular philosophers about religion, which takes place during Euler's second term at the Saint Petersburg Academy. In this Euler is supposed to use the non sequitur to Denis Diderot as proof of God : “My Lord! , so God exists. Answer me! ”, Whereupon he could not reply and left Russia humiliated. The anecdote is apocryphal since Diderot himself did research in mathematics. The legend was apparently told first by Dieudonné Thiébault (in his book Mes souvenirs de vingt ans de séjour à Berlin in 1801), with further strong decorations by Augustus De Morgan . This may have been done to highlight Euler's religious beliefs. However, no contemporary sources are available for the alleged incident.
Correspondence
Euler maintained extensive contacts and correspondence with many of the most important mathematical scientists of the time, including Christian Goldbach , Alexis Clairaut , Jean d'Alembert , Joseph Louis Lagrange, and Pierre Simon Laplace . There was a friendly correspondence between Euler and Goldbach as well as Euler and Clairaut who dealt with current problems in number theory, mathematical analysis, differential equations, fluid mechanics and celestial mechanics. Neither differences of opinion nor claims of one against another dominated the exchange. Rather, they openly discussed all mathematical ideas and problems, often well before their publication.
Euler in Berlin and d'Alembert in Paris in particular had extensive mathematical correspondence over many years. In the year 1757 they finally had a strong difference of opinion, which led to an estrangement as to whether discontinuous or indifferentiable functions are permissible solutions to the vibrating string problem . There was also a priority dispute between them over the theory of precession , equinoxes, and the nutation of the earth's axis . After d'Alembert visited Euler in Berlin in 1763, their relationship became more familiar again. In 1759 the young Lagrange participated in the discussion of the solutions with a controversial article criticized by both Euler and d'Alembert. Lagrange, however, shared most of Euler's views. In 1761, Lagrange attempted to counter the criticisms of d'Alembert and others by providing a different treatment of the vibrating strings problem. The debate continued for another twenty years with no solution being found. The issues at issue were only resolved when Joseph Fourier took up the subject over the next century.
Although Euler made an important and pioneering contribution to the calculus of variations , Lagrange, at the age of 19, made the first formulation of the equations of analytical dynamics according to the principles of the calculus of variations, and his approach was superior to Euler's semi-geometric methods. The classic Euler-Lagrange variation problem of determining the extreme value of a functional analysis led to the famous Euler-Lagrange equation .
The scientific correspondence was based primarily on numerous letters. There was particularly lively exchange with Jean d'Alembert (at least 39 letters), Daniel Bernoulli (at least 100 letters), Johann I Bernoulli (at least 38 letters), Alexis Clairaut (at least 61 letters), Christian Goldbach (at least 196 letters) and Pierre Louis Maupertuis (at least 129 letters, 124 of them from Euler).
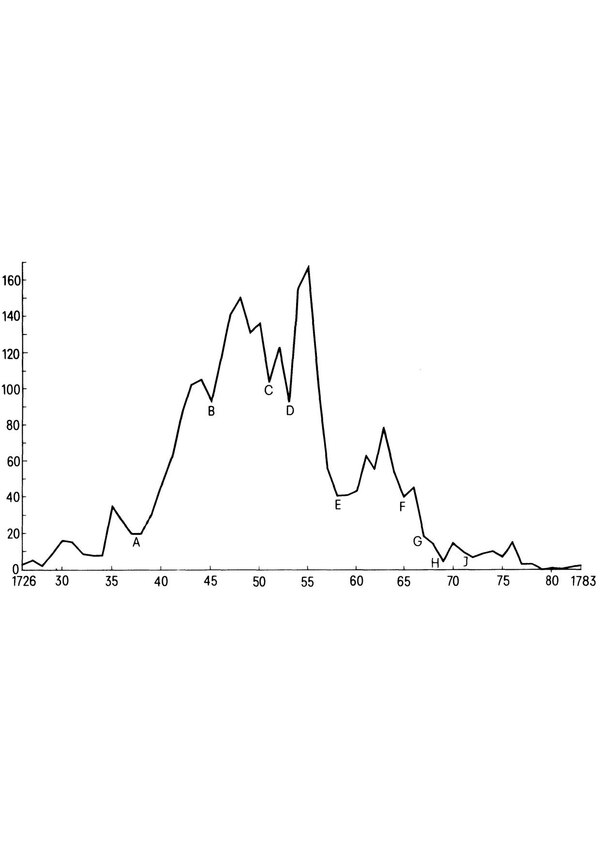
Legend in the upper graphic:
A: Euler fell seriously ill in 1738 and lost the sight of his right eye.
B: The Berlin Academy was opened in January 1745, and Euler, who had been in Berlin since 1741, had a lot of administrative work to do as director of the mathematical class. He also got seriously ill that year.
C: The grueling controversy between Maupertuis and JS Koenig took place in 1751/52, which led to the “academy dispute”.
D: In 1753 Maupertuis took a leave of absence and traveled to France. Euler is responsible - unofficially, but de facto - the management of the academy.
E: The Seven Years' War (1756–1763) largely prevented - at least in the first half - postal traffic.
Q: Euler's falling out with Frederick II, which finally
G: 1766 leads to Euler's departure for Petersburg.
H: Euler has to reorganize himself, severely handicapped by the worsening cataract in his left eye.
J: 1771 complete loss of vision (complete blindness ).
reception
Contemporary
Euler's reputation and influence were already extremely great during his lifetime. For about two decades he was the "spiritual leader of the educated circles" in the Protestant part of Germany. He performed important services as the "golden bridge between two academies", of which his correspondence is just as impressive as the fact that 109 publications from his pen came from his pen during his time in Berlin 1741–1766 in the Petersburg files (the journals of the academy). opposite 119 in the memoirs of the Prussian Academy. In total, Euler won twelve international academy prizes, not counting the eight prizes of his sons Johann Albrecht (7) and Karl (1), to which he made decisive contributions. Louis XVI gave him 1,000 rubles for his second ship theory , and Catherine II gave him twice that amount.
Euler's first theory of the moon had a practical consequence that should not be underestimated: in 1755, the Göttingen astronomer Tobias Mayer compiled lunar tables based on Euler's formulas , which allowed the position of the earth's satellite and thus the geographical length of a ship on the high seas to be reached with something that had never been achieved in navigational science Determine exactness. In 1714, the British Parliament had offered a considerable monetary prize for determining the length on the high seas below an error limit of half a degree. This prize was first awarded in 1765: Mayer's widow received £ 3,000 , and Euler £ 300 for the theory on which the Mayer tables were based. These lunar tables were included in all navigational almanacs and the method was used in seafaring for more than a century.
Pierre-Simon Laplace is said to have said to his students:
«Lisez Euler, c'est notre maître à tous! »
"Read Euler, he is all of us master!"
In the 19th century
Euler's books, which, according to Emil Fellmann, “are consistently characterized by the highest striving for clarity and simplicity” and “represent the first actual textbooks in the modern sense”, established Euler not only as “the teacher of Europe of his time”, but well into the 19th century into it: the works of Bernhard Riemann , for example, have "unmistakable Eulerian features". Henri Poincaré reports that, according to Theodore Strong, “Euler is the god of mathematics, whose death marks the decline of the mathematical sciences”.
In contrast to this, Euler's teachings of “two matters”, one “coarse” and one “subtle”, to which all phenomena can be traced back, met with rejection in the 19th century. Accordingly, they were not pursued further during this time. Euler's thoughts on such a duality were published posthumously in his guide to the theory of nature . The "coarse matter" is responsible for "various substances" (the exact investigation of which Euler left to chemistry ) and the "subtle matter" (an ether ) for gravity , electricity , magnetism and optics . However, it is possible that Bernhard Riemann studied the instructions and was influenced by them.
Euler's writings are said to have had a very special influence on Carl Gustav Jacobi , one of the most important mathematicians of the 19th century. He collected Euler's books, studied them eagerly, and remarked in a letter to his brother in 1849:
"It is wonderful that even today one reads each of his treatises not just with instruction, but with pleasure."
He tried in vain to obtain Euler's two volumes, Opuscula analytica , published in Petersburg in 1783 and 1785 . When Euler's great-grandson Paul Heinrich von Fuss sent him the volumes from Petersburg, Jacobi replied to him in a letter on May 3, 1841:
“I first saw them [the two volumes] two years ago at Crelle's and immediately discovered something that Dirichlet and I had previously taken to be our property; other things, in that they fertilize old ideas of mine, may lead me to an interesting discovery. "
For Jacobi, Euler's writings became a “treasure trove of stimulation” and his results and methods led Jacobi to new “astute discoveries”. This relates above all to the triple product found by Jacobi , which he described as “probably the most important and fruitful thing that [he] invented in pure mathematics”. This is a direct generalization of Euler's pentagonal theorem and has important consequences for the theory of theta functions .
Carl Friedrich Gauß praised Euler's work and emphasized its value for future generations of mathematicians:
“No other mathematician, older or more recent, can boast such an almost incomprehensible speed in the most difficult work with such an inexhaustible fertility of new ideas and resources. He worked on all parts of the math, and most of them were given a completely new shape in his hands. "
In the 20th century until today
From the point of view of today's scientific history, Leonhard Euler is given a very important role in relation to the progress of mathematics and technology. With regard to his not sometimes strict execution of analytical techniques, however, "logical gaps" are occasionally criticized. In particular, his handling of the infinitely great met with criticism, although he is often said to have great “analytical power” because of the correct end results despite everything.
Ronald Calinger places the Euler phenomenon and his achievements in the history of science as follows: In mathematics, only a few great new achievements or fundamental innovations were expected with the beginning of the Enlightenment. The 17th century - when most of the experts in the field came from the aristocracy or held positions in medicine, law, or religion - was considered a "golden age" of mathematics. By the middle of the century, René Descartes and Pierre de Fermat had independently created what is now called analytic geometry . This period culminated in the beginnings of calculus in the Method of fluxions of Newton and the work of Gottfried Wilhelm Leibniz . Many now assumed that there was little left of general concern to follow. But other scholars instead anticipated a “fertile era” not only in analysis, including the creation of its core branches, but in all of mathematics, both in theory and in application. Above all, Leonhard Euler's extensive research and writings were intended to ensure that all of this would happen. Driven by "tremendous energy," a "passion for mathematics" and the exact sciences, a "commitment" to building a "strong institutional base" for these fields, and a "persistent defense" of Reformed Christianity , Euler has pursued ever since Time in Basel, with the exception of a few severe attacks of fever, “diligently” an “immense research, arithmetic and writing program” in pure and applied mathematics and related fields. In the calculus of differential calculus alone, he provided hundreds of discoveries and proofs, along with many “fearless” calculations to simplify and clarify techniques for differential calculus , infinite series, and integral calculus . He was the main inventor of the core branches of differential equations in a semi-geometric analytical form and (together with Lagrange) later the analytical calculus of variations . In hundreds of articles and an analysis trilogy, beginning with the two-volume Introductio in analysin infinitorum (Introduction to the Analysis of the Infinite, E101 and E102, 1748), Euler laid the foundations: these were “methodically arranged”, “worked out” and "Conveyed as a calculation". He thus laid the foundation for the initial program for the development of calculus . As a primary result of his studies, analysis replaced Euclidean geometry from its two millennia dominance in mathematics and was the model for reason in the esprit géométrique of the epoch. In pure mathematics, Euler did more: he made "substantial progress" in number theory , algebra , combinatorics , graph theory , probability theory , topology and geometry , as well as pioneering work in the differential geometry of surfaces. Euler was also "deeply rooted" in the exact sciences of mechanics, optics and astronomy and made contributions to applied mathematics that were "unparalleled" in their combination of scope and depth.
Euler's analysis from today's perspective
According to Alexander Gelfond , for Leonhard Euler mathematics was "inseparably connected with its applications". In the search for an algorithm for solving tasks, "first and foremost methods that lead to the goal with the most convenient, practical and simple operations" were. Euler saw mathematics as a “powerful tool” that is “indispensable” for searching for solution algorithms. This would have always been in the foreground and determined “the algebraic and constructive coloring” of the methods that Euler introduced into analysis.
With regard to the concept of the infinite , Euler carried out “instead of any exact definitions long philosophical explanations” which “did not illuminate the essence of the question”. However, when dealing with infinitely increasing or decreasing sizes, he “doesn't make any mistakes” because he always takes into account the “rapidity of increasing or decreasing” these sizes when they give him e.g. B. encounter in the form of relationships. In various places he speaks "also about the infinite infinitely great order in comparison to another infinite". In his work De summa seriei ex numeris primis formatae , for example , he says that “the infinite that is through the series
the logarithm of that infinite arises which is represented by the harmonic series
is represented ". Thus “the second infinity is of an infinitely higher order than the first”. He said he always “avoided” problems with a lack of convergence (for example with values of the Riemann zeta function in negative places) by, among other things, “using the so-called Abelian summation method” and thus “anticipating it by a century”. In this context Detlef Laugwitz notes Euler's habit of identifying like
or
to have used (whereby here “is greater than any finite number”), which “gave rise to some criticism”. Because of Euler's weaknesses in dealing with the infinite, Emil Fellmann refers to the lack of an axiomatic introduction of real numbers :
“Certainly, one has often - almost always wrongly - pointed to supposedly clear weaknesses in Euler's work, mainly to the supposedly inadmissible jumping around with the concept of the infinite, be it on a large scale (series theory) as well as on a small scale. He could not care at all about criteria of convergence and continuity in the modern sense as well as about the logically exact and coherent foundation of analysis in the sense of the ars demonstrandi of Cauchy, Bolzano or Weierstrass, because a (in today's sense) strict evidence for Cauchy's The convergence criterion was only made possible after a definition of the real numbers - i.e. 1870 at the earliest. Euler relied - only occasionally unsuccessfully - on his astonishing instinctual security and algorithmic power. "
Thomas Sonar emphasizes in a special way the importance of Euler's "zero calculation" as a great achievement. Euler brought this “to the highest perfection”. Sonar refers, among other things, to Leibniz's contributions to the theory of movement, in which “rudiments and beginnings of lines and figures” are mentioned, which are “smaller than any specifiable size”. In a “virtuoso” way, Euler would succeed with this tool, as correctly known infinite series for the exponential function and the logarithm, but also derivatives such as
derive.
Assessment of the way of working and productivity
The science historian Emil Fellmann names three key components regarding the phenomenon of productivity and working methods. First, Euler would have had “the gift of a probably unique memory ”. What Euler had ever heard, seen or written seems to have “forever stuck in his mind”. There are "innumerable contemporary testimonies" of this. Even in old age he is said to have "delighted his family members, friends and societies with the verbatim recitation of any chant from Virgil's Aeneid , and even decades later he knew the minutes of the academy meetings by heart - not to mention his memory for mathematical matters." Fellmann emphasizes Euler's “rare ability to concentrate” as a second point. Noise and activity in his immediate vicinity would have "hardly bothered him in his thought work". The quote: "A child on his knees, a cat on his back, this is how he wrote his immortal works" is said to have come down to us from Dieudonné Thiébault . The third key is “quite simply constant, calm work”.
Honors

Namesake for prizes and awards
Several mathematics prizes are named after Leonhard Euler. Since 1991, the Russian Academy of Sciences has awarded the Leonhard Euler Gold Medal for particularly outstanding achievements in the fields of mathematics and physics. For special achievements in the field of combinatorics that lends Institute of Combinatorics and its Applications annually the so-called. Since 1993 Euler Medal .
Also named after Leonhard Euler is the Euler Book Prize , which is awarded annually by the Mathematical Association of America for “an excellent book on mathematics”.
Exhibitions, colloquia and lectures
On the 200th year of his death, in 1983, the Technical University of Berlin organized an Euler Colloquium , in which Emil Fellmann , Erhard Heinz , Olli Lehto and Kurt Strebel gave lectures.
On the occasion of his 300th birthday, the Landesmuseum Braunschweig dedicated an exhibition and lecture series to Leonhard Euler. The focus was "in researching, presenting and conveying questions of the history of science to cooperation between different disciplines, for which the" Project Euler "was an excellent choice." The exhibition report also states:
"Euler was not only an outstanding scientist of international importance, but also a personality who, as early as the 18th century, led a life closely connected to the scientific centers of Europe."
Other exhibitions held u. a. the University of Basel and the University of Würzburg .
Popular science
The Euler's identity in the form has been prepared by Nobel laureate Richard P. Feynman as "the most remarkable formula in mathematics" means exactly because of their unique use of addition , multiplication , power and equality as well as the one-time use of the important constants 0, 1, e , i and π. In 1988 the readers of the Mathematical Intelligencer voted it (in the form ) the "most beautiful mathematical formula of all time". Overall, Euler was responsible for three of the five best formulas in this survey: the polyhedron substitution came in second and the Basel problem came in fifth
Euler is the namesake of the so-called Project Euler , a website on which a number of problems are posed, which mostly have to be solved by means of mathematical programming. The aim of the project is to support interested people in deepening their programming skills in a playful way or in refreshing what they have already learned.
The Euler Disc (English Euler's Disc ) is a physical toy for demonstrating the energy dissipation of a rotating disc. The disc was invented around 1987 by Joe Bendik, who named it after Leonhard Euler because Euler had already dealt with mathematical aspects of this physical problem.
Leonhard Euler Telescope
Also named after Euler is the Leonhard Euler Telescope, a reflector telescope with a 1.2 m aperture of the Geneva Observatory at the La Silla Observatory of the European Southern Observatory.
Leonhard Euler as namesake
Methods or ideas developed by Leonhard Euler that bear his name are:
Equations:
- Euler-Bernoulli equation, fourth order differential equation on which the continuum mechanics of the beam is based, see bending line (part of the Euler-Bernoulli beam theory)
- Euler's differential equation , linear ordinary differential equation of any order
- Euler's equations of fluid mechanics , basic equations for the dynamics of ideal (frictionless) liquids
- Euler's gyroscopic equations
- Euler-Lagrange equation
- Euler-Lotka equation
Formulas:
- Euler-Eytelwein formula , formula for rope adhesion
- Euler's formula
- Euler's formula or Euler's theorem in surface curvature, see principal curvature
- Euler-Maclaurin Formula
- Euler-Rodrigues formula
- Euler's series
- Euler product
Theorems and theorems:
- Euler's theorem , theorem in economics
- Euler-Fermat theorem (number theory)
Constants and number sequences:
- Euler-Mascheroni constant , and Euler's constant called
- Euler's number
- Euler numbers , related to the Bernoulli numbers , appear as Taylor coefficients of secant hyperbolic function on
- Euler numbers form the Euler triangle similar to Pascal's triangle in combinatorics
- Euler's number is a dimensionless number in fluid mechanics
- Euler's pseudoprime number
Assumptions:
- Euler's conjecture , conjecture of number theory and generalization of Fermat's conjecture
Functions and (mathematical) procedures:
- Euler's integral of the first and second genus ( Euler's beta function and gamma function )
- Euler-Maruyama method for solving stochastic differential equations
- Euler's polygon method (integration method for differential equations)
- Euler's Phi function = number of prime numbers to be coprime with
- Euler's series transformation
- The Euler product is sometimes referred to as the Euler function in the theory of the partition function (see also Pochhammer symbol ).
- Euler's criterion for calculating the Legendre symbol
- Euler's substitution in integral calculus
Geometry and topology:
- Euler's straight line : the straight line connecting the center of gravity, vertical intersection and circumcenter of a triangle
- Euler's theorem (geometry)
- Euler's theorem (quadrangular geometry)
- Euler's triangle , a special shape of the spherical triangle
- Euler brick , a cuboid with integer lengths of the edges and surface diagonals
- Euler's polyhedron substitute
- Euler's angle
- Euler characteristic , in topology a key figure for closed surfaces
- Euler cradle , a cardanic suspension that can be rotated in all three Euler's angles
- Euler class
Graph theory:
- Euler-Hierholzer theorem
- Euler's line (also "Eulertour" or "Euler's circle"), a line of edges that contains every edge of a graph
Music theory:
- Euler's tone network , representation of the range of the pure tuning in a two-dimensional grid of pure fifths and thirds
Physics and Mechanics:
- Euler-Bernoulli beam theory, see Bernoulli's assumptions
- Euler's buckling cases
- Euler's turbine equation as the basis for the engine of modern power generation
- Euler's load in beam theory is the minimum axial load required to cause a deflection
- Euler gyro
- Euler force
- Euler wind
Other honors and dedications

The Evangelical Lutheran Church in America commemorates Leonhard Euler with a memorial day on May 24th, together with Nicolaus Copernicus .
In 1875 a bust in honor of Leonhard Euler was erected at the entrance to the Bernoullianum in Basel . A text board indicates that the Bernoullianum was built in the years 1872-74 by Johann Jakob Stehlin the Younger (1826-94) for the 400th anniversary of the university for the natural sciences on the area of the Wasen bulwark built in 1530.
A commemorative plaque on Behrenstrasse 21/22 , which is now the building of the Bavarian Representation in Berlin, was erected in 1907 to commemorate his work and his former home in Berlin .
Since 1976, the front of the 10 Swiss franc banknote has shown Euler's portrait. The motif of the bill on the back showed a water turbine (one with high efficiency was first constructed by Euler), our solar system and the beam path in a lens system . In the reserve series designed in the 1980s (so-called secret reserve , which would have come into circulation in the event of mass counterfeiting), Leonhard Euler was also shown on the 10 franc note. However, both the portrait and the subject changed. The gamma function , the solar system and a table of numbers in the background are shown on the reserve note.
10 Swiss francs - note from 1976 to 1995
10 Swiss franc - Note (reserve series from 1984)
Furthermore, a lunar crater ( Euler crater ) and the asteroid (2002) Euler are named in his honor . The latter happened in 2002 in recognition of “his contributions to mathematics and science”.
A software for numerical and symbolic calculations ( Euler Math Toolbox ) also bears his name. The plant genus Euleria Urb. from the sumac family (Anacardiaceae) was named after him in 1925.
Leonhard Euler has been honored several times on postage stamps: in Switzerland in 1957 and 2007, in the GDR in 1950, 1957 and 1983 and in the Soviet Union in 1983. In 2007 a commemorative coin was issued in Russia in honor of Euler.
Streets in Basel and Berlin, among others, were named after Leonhard Euler.
Fonts
Publications (selection)
- Mechanica sive motus scientia analytice exposita. 2 volumes, 1736 ( E015 , E016 ).
- Tentamen novae theoriae musicae . 1739 ( E033 ).
- Introduction to the art of arithmetic for the use of the Gymnasii at the Imperial Academy of Sciences in St. Petersburg. 2 volumes, Academische Buchdruckerey, Saint Petersburg; Volume 1 1738, Volume 2 1740. ( Digitized version and full text in the German Text Archive Volume 1, digitized version and full text in the German Text Archive Volume 2).
- Solutio problematis ad geometriam situs pertinentis. 1741 ( E053 ).
- Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti. 1744 ( E065 ).
- Introductio in analysin infinitorum. 2 volumes, 1748 ( E101 , E102 ).
- Découverte d'un nouveau principe de Mécanique. In: Mémoires de l'académie des sciences de Berlin. Volume 6, 1752, pp. 185-217 ( E177 ).
- Institutiones calculi differentialis. 2 volumes, 1755 ( E212 ).
- Theoria motus corporum solidorum seu rigidorum. 1765 ( E289 ).
- Lettres à une princesse d'Allemagne. 3 volumes, 1768 ( E343 , E344 , E417 ).
- Institutiones calculi integralis. 3 volumes, 1768–1770 ( E342 , E366 , E385 ).
- Complete guide to algebra. 2 volumes, 1770 ( E387 , E388 , volume 2 digitized and full text in the German text archive ).
German translations and editions of his works
- Leonhard Euler's complete guide to integral calculus , Ed. Joseph Solomon, 3 volumes, Vienna 1828 to 1830 (Volume 1 e-rara.ch , Volume 1 archive.org , Volume 2 archive.org , Volume 3 archive.org ).
- Leonhard Euler's Mechanics or Analytical Presentation of Science, 3 volumes, Ed. J. Ph. Wolfers, Greifswald 1848 to 1853 (Volume 1 archive.org , Volume 2 archive.org , Volume 3 archive.org ).
- Euler, Johann Bernoulli, Jacob Bernoulli: Treatises on the calculus of variations, 1st part, Ostwalds Klassiker 46, Leipzig 1894 ( archive.org ).
- Euler: Two treatises on spherical trigonometry, Ostwalds Klassiker 73, Leipzig 1896 ( archive.org ).
- Euler: Three treatises on map projection, Ostwalds Klassiker 93, Leipzig 1898 ( archive.org ).
- Jakob Bernoulli, Leonhard Euler: Treatises on the equilibrium and the vibrations of the flat elastic curves, Ostwalds Klassiker 175, Leipzig 1910
- Euler: More complete theory of machines that are set in motion by the reaction of water (1754), Ostwalds Klassiker 182, Leipzig 1911
- Euler: Three papers on the solution of equations (1783, 1764, 1790) , Ostwalds Klassiker 226, Leipzig 1928
- Euler: Introduction to the Analysis of Infinite, Part 1, Introduction Wolfgang Walter, Springer 1983
- Euler: On the theory of complex functions, introduction by AP Juschkewitsch, Ostwalds Klassiker 261, Akademische Verlagsgesellschaft 1983
Opera Omnia
Euler published around two dozen books and 500 scientific articles. The German mathematician Ferdinand Rudio (1856–1929) initiated the publication of all of Euler's works. More than 30 volumes were published during Rudio's lifetime. Over 70 individual volumes had been published by 2013, as well as four volumes from the extensive correspondence. The works appear in the original language, mostly French or Latin.
The collected works have been published as Opera Omnia by Birkhäuser (Springer) Verlag since 1911 by the Euler Commission , which was founded by Ferdinand Rudio. At that time Adolf Krazer , Rudolf Fueter , Heinrich Weber , Paul Stäckel and Karl von der Mühll were also involved in the publication. The later editors of individual volumes included Ludwig Schlesinger , Friedrich Engel , Andreas Speiser , Clifford Truesdell (physics, mechanics, the whole volume 11-1 is a history of elasticity theory in the 17th and 18th centuries, written by Truesdell), Alexander Mikhailovich Lyapunow , Georg Faber , August Gutzmer , Carl Boehm , Constantin Carathéodory , Henri Dulac , Max Herzberger , Emile Cherbuliez , Charles Blanc and Eric Aiton (physics). After Rudio, the main editors were Andreas Speiser (from 1928), Walter Habicht (from 1965) and, since 1985, Hans-Christoph Im Hof . Other editors included Emil Fellmann , Adolf Juschkewitsch , Henri Dulac, Pierre Costabel , René Taton , Wladimir Iwanowitsch Smirnow , Alot T. Grigorjan, Joachim Otto Fleckenstein , Johann Jakob Burckhardt , Gleb K. Mikhailov, Franz Lemmermeyer , Andreas Kleinert and Martin Mattmüller .
The edition consists of
- Row 1: Mathematics, 30 volumes (complete). The first volume in 1911 was the manual for algebra. Volume 16 consists of two volumes.
- Series 2: Mechanics and Astronomy, 27 volumes in 30 partial volumes (complete).
- Row 3: Physics and Others, 12 volumes (complete).
- Row 4a: Correspondence. Planned: 10 volumes for around 3100 letters with around 300 correspondents. Published so far: 4 volumes.
- Row 4b: notebooks, diaries and unpublished items (planned).
Letters
During the correspondence of the Opera Omnia appeared:
- Volume 1 (summary of contents, overview, 1975),
- Volume 2 (with Johann I. and Nikolaus I. Bernoulli),
- Volume 5 (with Clairaut , d'Alembert and Lagrange ) and
- Volume 6 (with Maupertuis and Friedrich II.).
In addition, the following correspondence has appeared outside the Opera Omnia :
- with Goldbach (Akademie Verlag, Berlin 1965),
- with the Berlin and Petersburg academies (Akademie Verlag, Berlin, 3 volumes: 1959, 1961, 1976),
- with Tobias Mayer (American Elsevier, 1971).
In 1845 Paul-Heinrich Fuss published parts of Euler's correspondence with Goldbach, Nikolaus Fuss , Johann I, Nikolaus and Daniel Bernoulli. Volume 14 of Lagrange's edition also includes the correspondence with Euler.
literature
Monographs and edited volumes
- Gerd Biegel , Angela Klein, Thomas Sonar (eds.): Leonhard Euler. 1707-1783. Mathematician - Mechanic - Physicist (= Disquisitiones historiae scientiarum. Braunschweig Contributions to the History of Science. Vol. 3). Braunschweigisches Landesmuseum, Braunschweig 2008, ISBN 978-3-927939-79-0 .
- Nikolai Nikolajewitsch Bogoljubow , Gleb K. Michailow, Adolf Juschkewitsch : Euler and modern science. Mathematical Association of America, 2008.
- Robert E. Bradley, C. Edward Sandifer (Eds.): Leonhard Euler: Life, Work and Legacy. Elsevier 2007.
- Horst Bredekamp , Wladimir Velminski (ed.): Mathesis & Graphe. Leonhard Euler and the Development of Knowledge Systems. Akademie-Verlag, Berlin 2010, ISBN 978-3-05-004566-5 .
- Ronald S. Calinger: Leonhard Euler. Mathematical Genius in the Enlightment , Princeton University Press 2015
- Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. Imperial College Press, London 2010.
- William Dunham : Euler: The Master of Us All. Mathematical Association of America, 1999, ISBN 0-88385-328-0 .
- William Dunham (Ed.): The Genius of Euler. Reflections on his life and work , Mathematical Association of America 2007
- Emil Fellmann (Ed.): Leonhard Euler 1707–1783. Contributions to life and work. Commemorative volume of the canton of Basel-Stadt. Birkhäuser, Basel 1983, ISBN 3-7643-1343-9 .
- Emil A. Fellmann : Leonhard Euler. Rowohlt, Reinbek 1995, ISBN 3-499-50387-5 .
- Emil Fellmann: Leonhard Euler , Birkhäuser 2007
- Xavier Hascher, Athanase Papadopoulos (ed.): Leonhard Euler: Mathématicien, physicien et théoricien de la musique. CNRS Editions, Paris 2015, ISBN 978-2-271-08331-9 .
- C. Edward Sandifer: How Euler did it. Mathematical Association of America 2007 (Sandifer monthly column in MAA Online 2003 to 2007).
- C. Edward Sandifer: How Euler did even more , Mathematical Association of America 2015
- C. Edward Sandifer: The early math of Leonhard Euler , Mathematical Association of America 2007
- Thomas Sonar : 3000 Years of Analysis , Springer, 2011.
- Otto Spiess : Leonhard Euler. A contribution to the intellectual history of the 18th century. Frauenfeld 1929.
- Wilhelm Stieda : Leonhard Euler's move from Berlin to St. Petersburg. Hirzel, Leipzig 1931 urn : nbn: de: hbz: 061: 1-13189 .
- Dieter Suisky: Euler as a physicist. Springer, Berlin 2009.
- Margaret B. W. Tent: Leonhard Euler and the Bernoullis: Mathematicians from Basel. 2009, ISBN 978-1-56881-464-3 .
- Rüdiger Thiele : Leonhard Euler. (= Biographies of outstanding natural scientists, technicians and medical professionals . Volume 56) B. G. Teubner, Leipzig 1982, ISBN 3-322-00576-3 .
- VS Varadarajan : Euler through time: A new look at old themes. American Mathematical Society, 2006.
- Andreas Verdun: Leonard Euler's work on celestial mechanics , Springer Spectrum 2015
- Wladimir Velminski (Ed.): Leonhard Euler. The birth of graph theory. Kulturverlag Kadmos, Berlin 2009, ISBN 3-86599-056-8 .
- Rudolf Wolf : Leonhard Euler of Basel. In: Biographies on the cultural history of Switzerland. Fourth cycle. Orell, Füssli & Comp., Zurich 1862, pp. 87-134 ( books.google.de ).
Others
- Hannelore Bernhardt : Leonhard Euler - life and work. An introduction. Meeting reports of the Leibniz Society of Sciences in Berlin , Volume 94, pp. 15–31. trafo Wissenschaftsverlag Dr. Wolfgang Weist, Berlin 2008.
- Gustaf Eneström : Directory of Leonhard Euler's writings. Supplementary volume 4 to the annual report of the DMV. B. G. Teubner, Leipzig 1910 (first delivery), 1913 (second delivery) - ( archive.org ).
- Günther Frei : Number Theory, Analysis and Much More - The Significance of Leonhard Euler for Today. In: Naturwissenschaftliche Rundschau. Volume 60 (12). 2007, ISSN 0028-1050 . Pp. 629-635.
- Rüdiger Thiele: The Mathematics and Science of Leonhard Euler (1707–1783). Chapter 5 in Glen van Brummelen, Michael Kinyon (Ed.): Mathematics and the Historian's Craft. Springer, New York 2005, ISBN 978-0-387-25284-1 , pp. 81-140.
- André Weil : Number theory - a walk through the history from Hammurabi to Legendre. Birkhäuser 1992.
- Patricia Radelet-de Grave: The Problem of the Elastica Treated by Jacob I Bernoulli and the Further Development of this Study by Leonhard Euler. In: Karl-Eugen Kurrer , Werner Lorenz , Volker Wetzk (eds.): Proceedings of the Third International Congress on Construction History. Neunplus, Berlin 2009, ISBN 978-3-936033-31-1 , pp. 1209-1217 ( bma.arch.unige.it PDF).
reference books
- Moritz Cantor : Euler: Leonhard . In: Allgemeine Deutsche Biographie (ADB). Volume 6, Duncker & Humblot, Leipzig 1877, pp. 422-431.
- Andreas Speiser : Euler. Leonhard. In: New German Biography (NDB). Volume 4, Duncker & Humblot, Berlin 1959, ISBN 3-428-00185-0 , p. 688 f. ( Digitized version ).
- Emil A. Fellmann : Euler, Leonhard. In: Historical Lexicon of Switzerland .
- AP Youschkevitch: Euler, Leonhard . In: Charles Coulston Gillispie (Ed.): Dictionary of Scientific Biography . tape 4 : Richard Dedekind - Firmicus Maternus . Charles Scribner's Sons, New York 1971, p. 467-484 .
Web links
- Literature by and about Leonhard Euler in the catalog of the German National Library
- Works by and about Leonhard Euler in the German Digital Library
About Euler
- Euler Commission of the Swiss Academy of Sciences
- Euler 2007
- Rubric at MAA by Ed Sandifer "How Euler did it"
- John J. O'Connor, Edmund F. Robertson : Leonhard Euler. In: MacTutor History of Mathematics archive .
- Genealogy of Leonhard Euler's
- WDR report on the 225th anniversary of Euler's death
- 300 years of Leonhard Euler (Berlin-Brandenburg Academy of Sciences)
- Mathematical calendar in the spectrum of science (PDF; 849 kB)
- various essays on Euler in the BAMS 2007
- Music translated into Mathematics: Leonhard Euler
- Günther Frei: On the 300th birthday of Leonhard Euler. Hombrechtikum March 15, 2007 (PDF; 656 kB)
- Euler, Leonhard , in Heidelberg texts on the history of mathematics
- Video about Leonhard Euler's life .
- Bulletin of the AMS, Volume 44, 2007, Issue 4 , with essays on Euler (Varadarajan, Euler and his work on infinite series, Burt Totaro, Euler and algebraic geometry, George Andrews, Euler's De partitio numerorum, Harold Edwards, Euler's definition of the derivative)
From Euler
- Collected writings in the Euler archive of the MAA (English user guidance, also with texts on Euler and his environment)
- Introduction to the Analysis of the Infinite (German translation)
- Digitized writings on Euler's work in Berlin (BBAW)
- Correspondence with Friedrich II. - Digital edition of the Trier University Library
Individual evidence
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2015, p. 11.
- ^ Thomas Sonar: 3000 Years of Analysis. Springer, p. 448.
- ^ Rüdiger Thiele: Leonhard Euler. Leipzig, 1982. p. 16.
- ↑ Ioan James: Remarkable Mathematicians: From Euler to von Neumann. Cambridge, 2002, p. 2.
- ^ Ian Bruce: Euler's dissertation De Sono: E002. Translated & Annotated (PDF) .
- ^ A b c Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2015, p. 31.
- ↑ Ronald Calinger: Leonhard Euler: The First St. Petersburg Years (1727 to 1741). In: Historia Mathematica. Volume 23, No. 2, 1996, pp. 121-166, doi: 10.1006 / hmat.1996.0015 , p. 156.
- ↑ a b Ronald Calinger: Leonhard Euler: The First St. Petersburg Years (1727-1741). In: Historia Mathematica. 23, No. 2, 1996, pp. 121-166. doi: 10.1006 / hmat.1996.0015 , p. 125.
- ^ Peter Hoffmann: Leonhard Euler and Russia . In: Leonhard Euler: Life, Work and Legacy , p. 63
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2016, p. 68
- ↑ Ronald Calinger: Leonhard Euler: The First St. Petersburg Years (1727 to 1741) . Historia Mathematica. 23 (2), 1996, p. 126
- ↑ Ronald Calinger: Leonhard Euler: The First St. Petersburg Years (1727–1741) , Historia Mathematica 23 (2), 1996, p. 126
- ↑ Ronald Calinger: Leonhard Euler: The First St. Petersburg Years (1727-1741) . Historia Mathematica. 23 (2), 1996, pp. 128-129
- ^ IR Gekker, AA Euler: Leonhard Euler's family and descendants . In Nikolai Nikolajewitsch Bogoljubow , GK Michaĭlow, Adolf Pawlowitsch Juschkewitsch (eds.): Euler and Modern Science. Translated by Robert Burns. Mathematical Association of America, 2007, p. 402
- ↑ Nicolas Fuss: Eulogy of Euler by Fuss , accessed on Jan. 23, 2020
- ^ Genealogical list of the descendants of Leonhard Euler , euler.ch, accessed on February 20, 2020
- ^ Peter Hoffmann: Leonhard Euler and Russia . In: Leonhard Euler: Life, Work and Legacy , p. 63
- ↑ Leonhard Euler: Letters to a German princess on various subjects from physics and philosophy ; Vol. 1.
- ^ William Dunham: Euler: The Master of Us All. Mathematical Association of America. 1999, pp. XXIV-XXV
- ↑ Emil. René Bernoulli: Leonhard Euler's eye diseases . In: Leonhard Euler 1707–1783. Contributions to life and work , p. 473
- ^ Thomas Sonar: 3000 Year Analysis , Springer, 2011, p. 458
- ↑ David S. Richeson (2012). Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press, p. 17. Quoted by Howard W. Eves (1969). In Mathematical Circles: A Selection of Mathematical Stories and Anecdotes. Prindle, Weber, & Schmidt. P. 48
- ^ EA Fellmann: Leonhard Euler. Reinbek, 1995. pp. 85 f.
- ^ William Dunham: Euler: The Master of Us All. Mathematical Association of America, 1999, pp. XXIV-XXV
- ↑ Emil. A. Fellmann: Leonhard Euler's position in the history of optics . In: Leonhard Euler 1707–1783. Contributions to life and work , p. 310
- ^ Thomas Sonar: 3000 Years of Analysis , Springer, p. 457
- ↑ German in Karl Heinrich Siegfried Rödenbeck: Diary or history calendar from Friedrich's regent life (1740–1786). Vol. 3, pp. 182-183
- ^ Theodore Besterman (ed.): The Complete Works of Voltaire . tape 129 : Correspondence and related documents, XLV September 1777-May 1778, letters D20780-D21221 . The Voltaire Foundation, Banbury 1976, D21010, Frederick II to Voltaire, 25 January 1778, pp. 184-186 , here p. 185 (English). “ I wanted to make a jet of water in my garden; the Cyclop Euler calculated the effort of the wheels for raising the water to a basin, from where it should fall down through canals, in order to form a fountain jet at Sans-Souci. My mill was constructed mathematically, and it could not raise one drop of water to a distance of fifty feet from the basin. Vanity of Vanities! Vanity of mathematics. ”
- ^ M. Eckert: Euler and the Fountains of Sanssouci , Arch. Hist. Exact Sci. 56 (2002) 451-468., Pp. 451 ff.
- ^ Rüdiger Thiele: Leonhard Euler. Leipzig, 1982. p. 137
- ^ Thomas Sonar: 3000 Years of Analysis , Springer, p. 459
- ^ Leonhard Euler: Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum , E212, Dartmouth.
- ↑ Ronald S. Calinger: Leonhard Euler: Life and Thought . In: Leonhard Euler: Life, Work and Legacy , pp. 43–44
- ↑ Ronald S. Calinger: Leonhard Euler: Life and Thought . In: Leonhard Euler: Life, Work and Legacy , p. 47
- ↑ Ronald S. Calinger: Leonhard Euler: Life and Thought . In: Leonhard Euler: Life, Work and Legacy , p. 51
- ^ Edna Ernestine Kramer: The Nature and Growth of Modern Mathematics , Princeton University Press, p. 217
- ^ Fritz Nagel: Leonhard Euler and the Wonnen der Wissenschaft , accompanying text for the exhibition in the University Library of Basel from March 17th. until June 9, 2007, p. 15
- ↑ Ronald Calinger: Leonhard Euler mathematical genius in the Enlightenment . Princeton University Press, 2016, p. 8
- ↑ Ronald S. Calinger: Leonhard Euler: Life and Thought . In: Leonhard Euler: Life, Work and Legacy , p. 53
- ^ Peter Hoffmann: Leonhard Euler and Russia . In: Leonhard Euler: Life, Work and Legacy , p. 69
- ↑ Ronald Calinger: Leonhard Euler mathematical genius in the Enlightenment . Princeton University Press, 2016, p. 487
- ↑ Ronald S. Calinger: Leonhard Euler: Life and Thought . In: Leonhard Euler: Life, Work and Legacy , p. 52
- ↑ Ronald S. Calinger: Leonhard Euler: Life and Thought . In: Leonhard Euler: Life, Work and Legacy , p. 52
- ^ Genealogical list of the descendants of Leonhard Euler. Online at: Euler.ch. (PDF; 1.0 MB), accessed December 24, 2016.
- ^ Leonhard Euler: in the book of members of the AAAS
- ^ Leonhard Euler: Life, Work and Legacy , edited by Robert E. Bradley, Ed Sandifer, p. 56
- ↑ Marquis de Condorcet: Leonhard Euler's letters on various subjects from the theory of nature . tape 1 , p. XIX ( limited preview in Google Book Search).
- ^ Leonhard Euler: Life, Work and Legacy , edited by Robert E. Bradley, Ed Sandifer, p. 57
- ^ Thomas Sonar: 3000 Years of Analysis. Springer, p. 448.
- ↑ N. Fuss: Speech to Mr. Leonhard Euler , digitized version of the Bayerische Staatsbibliothek, Munich, pp. 106-107.
- ↑ Werner Schaal: Eulogy for a great mathematician . In: Research Center for Personal Writings (Academy of Sciences and Literature Mainz), accessed on February 16, 2020
- ↑ Historical Lexicon of Switzerland (HLS) - entry on Alexander Euler , accessed on February 8, 2020
- ^ Thomas Sonar: 3000 Years of Analysis . Springer, p. 448.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler, A Tribute Tricentennial , p vii
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics , Springer, p. XI
- ↑ Walter Guatschi: Leonhard Euler: His Life, the Man, and His Works , SIAM Review, Vol 50, No. 1, pp 3-33.. Doi: 10.1137 / 070702710 , p.3
- ↑ James J. Tattersall: Elementary Number Theory in Nine Chapters , p. 18
- ^ W. Dunham: The Genius of Euler: Reflections on His Life and Work , p. 15
- ^ Herbert Pieper: The Euler of the 19th Century: CG Jacob Jacobi , Elements of Mathematics, Swiss Mathematical Society, 2005, p. 98
- ↑ Lokenath Debnath: The legacy of Leonhard Euler, A Tricentennial Tribute , p. Xix
- ^ Dunham, William (1999). Euler: The Master of Us All. Mathematical Association of America. P. 17
- ↑ Boyer, Carl B .; Merzbach, Uta C. (1991). A History of Mathematics. John Wiley & Sons. Pp. 439-45.
- ↑ Wolfram, Stephen. Mathematical Notation: Past and Future . Accessed January 25, 2020.
- ↑ Boyer, Carl B .; Merzbach, Uta C. (1991). A History of Mathematics. John Wiley & Sons, pp. 439-45.
- ^ Dunham, William (1999). Euler: The Master of Us All. Mathematical Association of America. Chapters 3 and 4.
- ^ Caldwell, Chris: The largest known prime by year , accessed January 26, 2020
- ^ AJ Lotka: Studies on the mode of growth of material aggregates. American Journal of Science, 24, pp. 199-216
- ^ RE Bradley: Euler's analysis of the Genoese lottery , 2004.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler, A Tribute Tricentennial , p 341
- ↑ Alexanderson, Gerald (July 2006): Euler and Königsberg's bridges: a historical view . Bulletin of the American Mathematical Society. 43 (4): 567-573, doi: 10.1090 / S0273-0979-06-01130-X . P. 567
- ^ Commentarii academiae scientiarum imperialis Petropolitanae , Euler Archive
- ↑ L. Euler: Solutio problematis ad geometriam situs pertinentis , Commentarii academiae scientiarum imperialis Petropolitanae (CASP), Vol. 8
- ↑ Alexanderson, Gerald (July 2006): Euler and Königsberg's bridges: a historical view . Bulletin of the American Mathematical Society. 43 (4): 567-573, doi: 10.1090 / S0273-0979-06-01130-X . P. 567
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy. P. 421.
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy. P. 430
- ^ Cauchy, AL (1813): Recherche sur les polyèdres - premier mémoire . Journal de l'École Polytechnique. 9 (Cahier 16): pp. 66-86.
- ↑ L'Huillier, S.-A.-J. (1861): Mémoire sur la polyèdrométrie . Annales de Mathématiques. 3: 169-89.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics , Springer, p. 10
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2016, p. 467
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics , Springer, p. 11
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics , Springer, p. 283
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment , p 384
- ↑ Christa Jungnickel, Russell McCormmach: Cavendish - The Experimental Life , p. 155
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , p. 67
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 361.
- ↑ L. Euler: Introduction to the Analysis of the Infinite: Part One , Springer Verlag Berlin Heidelberg GmbH, p. 11 (introduction to the reprint edition)
- ↑ Yearbook of the Shipbuilding Society , Bouger and Euler: To justify the theory of hydrostatic ship stability, Volume 98, 2004, p. 183
- ^ Peter Pesic: Music and the Making of Modern Science , p. 133.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work In: Leonhard Euler 1707 - 1783: Contributions to life and work , pp. 73-74
- ↑ Ronald S Calinger, Ekaterina (Katya) Denisova, Elena N Polyakhova: Leonhard Euler's Letters to a German Princess , IOP Concise Physics, Morgan and Claypool Publishers, 2019
- ↑ Leonhard Euler: Solution d'une question curieuse que ne paroit soumise à aucune analyze , 1766
- ↑ Lokenath Debnath: The legacy of Leonhard Euler, A Tribute Tricentennial , p 162
- ^ W. Breidert: Leonhard Euler and Philosophy . In: Leonhard Euler: Life, Work and Legacy , p. 98
- ↑ Ronald Calinger: Leonhard Euler: The First St. Petersburg Years (1727 to 1741) . Historia Mathematica. 23 (2), 1996: 121-66. doi: 10.1006 / hmat.1996.0015. , Pp. 153-154
- ↑ Nikolaus von Fuss: funeral speech for Euler. (No longer available online.) 1783, archived from the original on March 24, 2015 ; accessed on February 22, 2017 .
- ^ Leonhard Euler: Opera omnia , ser. IVA, vol. 1, correspondence , eds. Adolph Pavlovitch Jusˇkevicˇ et al., Basel: Birkhaüser, 1975. p. 115
- ^ Thomas Sonar: 3000 Years of Analysis , Springer, p. 462
- ^ Leonhard Euler: Opera omnia , ser. I, vol. 10, Institutiones calculi differentialis , ed. Gerhard Kowalewski, Leipzig: Teubner, 1913, esp. 69-71. P. 136
- ↑ Leonhard Euler: Salvation of Divine Revelation against the interjections of the Frey spirits . Leonhardi Euleri Opera Omnia (3rd edition), 1960. 12.
- ↑ Michael Raith: The father Paulus Euler. On the spiritual origin of Leonhard Euler , in Leonhard Euler 1707-1783 contributions to life and work . P. 465
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2015, p. 501
- ^ Jacques Marty: Quelques aspects des travaux de Diderot en Mathematiques Mixtes . Recherches Sur Diderot et Sur l'Encyclopédie. 4 (1), 1988: pp. 145-147.
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2015, p. 501
- ↑ Dirk J. Struik: A Concise History of Mathematics (3rd revised edition). Dover Books, 1967, p. 129
- ^ RJ Gillings: The So-Called Euler-Diderot Anecdote . American Mathematical Monthly. 61 (2), February 1954: pp. 77-80. doi: 10.2307 / 2307789.
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2015, p. 501
- ↑ Dirk J. Struik: A Concise History of Mathematics . Dover, Third Revised Edition, 1967, ( online copy ), p. 129
- ↑ Lokenath Debnath: The legacy of Leonhard Euler, A Tricentennial Tribute , pp. Ix – x
- ^ Leonhard Euler: Briefwechsel , Opera omnia, Series Quarta A, Vol, 1, pp. 505–509
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 32
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 32
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 33
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 71
- ↑ Dirk Jan Struik: Outline of the history of mathematics. Springer, p. 139.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 33
- ↑ David Speiser: Euler's writings on optics, electricity and magnetism . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 226
- ^ W. Ahrens: Correspondence between CGJ Jacobi and MH Jacobi. Leipzig 1907.
- ^ Herbert Pieper: The Euler of the 19th Century: CG Jacob Jacobi , Elements of Mathematics, Swiss Mathematical Society, 2005, p. 98
- ^ Herbert Pieper: The Euler of the 19th Century: CG Jacob Jacobi , Elements of Mathematics, Swiss Mathematical Society, 2005, p. 98
- ^ Herbert Pieper: The Euler of the 19th Century: CG Jacob Jacobi , Elements of Mathematics, Swiss Mathematical Society, 2005, p. 100
- ↑ KR Biermann: CF Gauß as a mathematics and astronomy historian. Historia Math. 10: 422-434 (1983).
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2016, pp. 1-2
- ↑ Aleksander O. Gelfond: About some characteristic features in L. Euler's ideas in the field of mathematical analysis and his introduction to the analysis of the infinite In: Leonhard Euler 1707–1783: Contributions to life and work , pp. 100–101
- ↑ Detlef Laugwitz: The non-standard analysis: ideas and methods of Leibniz and Euler . In: Leonhard Euler 1707–1783: Contributions to life and work , pp. 187–188
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 34.
- ^ Thomas Sonar: 3000 Years of Analysis . Springer, p. 415.
- ^ Thomas Sonar: 3000 Years of Analysis . Springer, pp. 462-464.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work . In: Leonhard Euler 1707–1783: Contributions to life and work , p. 31
- ^ Euler Book Prize , Mathematical Association of America, accessed February 29, 2020
- ^ Eberhard Knobloch: On the work of Leonhard Euler: Lectures at the Euler Colloquium in May 1983 in Berlin , Birkhäuser, 1984, p. XI
- ↑ Gerd Biegel, Angela Klein and Thomas Sonar (eds.): Leonhard Euler 1707 - 1783. Mathematician - Mechanic - Physicist , Disquisitiones Historiae Scientiarum. Braunschweig Contributions to the History of Science, Vol. 3. Braunschweigisches Landesmuseum. Braunschweig 2008, p. 9
- ^ Gerd Biegel, Angela Klein, Menso Folkerts, Karin Reich and Thomas Sonar: Euler exhibition in Braunschweig , communications from the German Mathematicians Association
- ^ Exhibition on Euler's life and work . Retrieved February 29, 2020
- ^ Exhibition for the 300th birthday of Leonhard Euler . Retrieved February 29, 2020
- ^ Richard Feynman: Chapter 22: Algebra . The Feynman Lectures on Physics, 1970. IS 10.
- ^ David Wells: Are these the most beautiful? Mathematical Intelligencer. 12 (3), 1990: 37-41. doi: 10.1007 / BF03024015
- ↑ Euler's Disc at Experimentis.de. Retrieved November 2, 2017.
- ↑ May 24th in the Ecumenical Lexicon of Saints. Online at: Heiligenlexikon.de. Retrieved December 24, 2016.
- ^ Gustaf Adolf Wanner : All about Basel's monuments. Basel 1975, p. 40 ff.
- ↑ Testimony to mathematicians : busts of Daniel, Jakob and Johann Bernoulli and Leonhard Euler in the Bernoullianum in Basel (Switzerland), accessed on May 16, 2020
- ↑ Ronald S Calinger, Ekaterina (Katya) Denisova, Elena N Polyakhova: Leonhard Euler's Letters to a German Princess , IOP Concise Physics, Morgan and Claypool Publishers, 2019, pp. 3–25
- ↑ Lotte Burkhardt: Directory of eponymous plant names . Extended Edition. Botanic Garden and Botanical Museum Berlin, Free University Berlin Berlin 2018. bgbm.org
- ^ Leonhard Euler's 300th birthday - Basel 2007 . Retrieved February 20, 2020
- ↑ Euleriana , Berlin-Brandenburg Academy of Sciences, accessed on February 19, 2020
- ↑ Clifford Truesdell: The rational mechanics of flexible elastic bodies 1638–1788. 1960.
- ↑ Hans-Christoph Im Hof, Andreas Kleinert and others: Leonhard Euler, Opera omnia. In: Birkhauser history of science. ( springer.com ) Retrieved December 24, 2016.
- ^ Andreas Kleinert, Matthias Mattmüller: Leonhardi Euleri Opera Omnia: a centenary project. EMS Newsletter, September 2007, ISSN 1027-488X (PDF; 1.88 MB), online at: Euler-2007.ch. Retrieved December 24, 2016.
- ↑ Lagrange, œuvre. Volume 14 ( gallica.bnf.fr ).
| personal data | |
|---|---|
| SURNAME | Euler, Leonhard |
| BRIEF DESCRIPTION | Swiss mathematician and physicist |
| DATE OF BIRTH | April 15, 1707 |
| PLACE OF BIRTH | Basel |
| DATE OF DEATH | September 18, 1783 |
| Place of death | St. Petersburg |














![{\ displaystyle \ gamma: = \ lim _ {n \ to \ infty} \ left [\ sum _ {k = 1} ^ {n} {\ frac {1} {k}} - \ log (n) \ right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c620651551faae57bd712deeb4763028000fd337)