With trigonometric functions or trigonometric functions (rare: circular functions or goniometric functions ) refers to mathematical relationship between angle and aspect ratios (originally in right-angled triangles ). Tables of ratio values for specific angles enable calculations for survey tasks that use angles and side lengths in triangles. The trigonometric functions are also the basic functions for describing periodic processes in the natural sciences.
Overview of the trigonometric functions
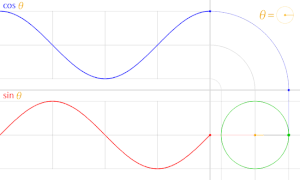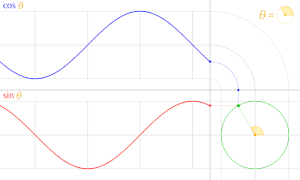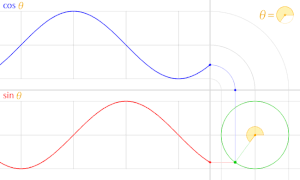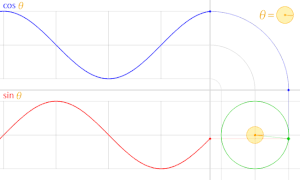
The animation shows the relationship between the unit circle and the sine and cosine functions

Trigonometric functions definable on the unit circle

The function graphs of all trigonometric functions
The elementary trigonometric functions are:
as well as their reciprocal values:
There are close connections between these functions. Strictly speaking, just one of the functions would be sufficient to solve any trigonometric problem. However, using several different functions allows the calculations and formulas to be simplified.
The cotangent function is often used in tables with function values of trigonometric functions, since cot ( x ) can be tabulated together with the tangent function. In this respect, the meaning of cot ( x ) is somewhat greater than that of sec ( x ) and csc ( x ).
There are other functions, which are rather unusual today, such as B. sinus versus ( versin ), cosinus versus ( coversin ) , exsecant ( exsec ) and excosecant ( excsc ) .
definition

Originally, the angle functions were defined as aspect ratios in right triangles and therefore only for angles from 0 to 90 degrees:

This definition is independent of the choice of right triangle that is used for the calculation. In every right-angled triangle with the same angle , these ratios give the same value. This can be done e.g. B. prove with the ray theorems.

From these relationships the relationship follows immediately:

The adjacent side of the angle is at the same time the opposite side of the other acute angle of the right triangle; since the sum of the angles in the triangle is 180 °, and the right angle adds 90 ° to this sum, this angle is and therefore



The angular functions can, however, be extended to larger angles as secant and tangent segments on the unit circle . From the point of intersection of one angle leg with the unit circle, the perpendiculars are drawn on the two coordinate axes and provide the sine and cosine of the angle. The tangents at points x = 1 and y = 1 also intersect the leg and then provide the tangent and cotangent in the projection onto the axes. The leg may have to be extended backwards in order to achieve an intersection. In this way, values of the trigonometric functions can be assigned to each angle from 0 to 360 degrees, which can of course also become negative (see figure). The relationships given above continue to apply.
In analysis, sine and cosine are usually defined using power series, with the angle being given in radians . For more information, see the articles sine and cosine and tangent .
Relationships between functions
The following table shows the signs of the trigonometric functions depending on the quadrant :
| quadrant
|
sin and csc
|
cos and sec
|
tan and cot
|
| I.
|
+
|
+
|
+
|
| II
|
+
|
-
|
-
|
| III
|
-
|
-
|
+
|
| IV
|
-
|
+
|
-
|
The amount is converted as follows:
|
|
sin
|
cos
|
tan
|
cot
|
sec
|
csc
|
| sin ( x )
|

|

|

|

|

|

|
| cos ( x )
|

|

|

|

|

|

|
| tan ( x )
|

|

|

|

|

|

|
| cot ( x )
|

|

|

|

|

|

|
| sec ( x )
|

|

|

|

|

|

|
| csc ( x )
|

|

|

|

|

|

|
If that is used, note that
-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

-
 for or
for or

Application of the trigonometric functions
The trigonometric functions are mainly used in surveying . Formulas for calculating sizes on the triangle → triangle geometry .
They are also important in analysis and in many applications in physics and technology . There is a close relationship to the exponential function , which is particularly visible in functions of complex numbers and in the Taylor series of functions.
Inversion of the trigonometric functions
In some situations the trigonometric functions are needed to calculate angles from aspect ratios. These are Inverse Trigonometric and inverse trigonometric functions arcsin , arccos , arctan and arccot - the inverse functions to the trigonometric functions - used. On calculators they are often denoted by sin −1 , and so on. This is consistent with the notation for the inverse function of f match (even if the Inverse Trigonometric the strictly speaking, are not), but collided with the equally usual convention for writing to.



The arc functions are used to calculate the angle for an aspect ratio. Because of the symmetry of the trigonometric functions, it has to be clarified on a case-by-case basis in which quadrant the desired angle lies.
See also
Web links





























































































