Arcsine and arcsine

Arc sine and arccosine in the Cartesian coordinate system

arcsin ( x )

arccos ( x )

The arcsine - written or  - and the arccosine (or also arccosine ) - written or  - are inverse functions of the (suitably) restricted sine or cosine function . Sine and cosine are functions that map an angle to a value in the interval ; as their inverse functions, arcsine and arcsine map a value from again to an associated angle. Since sine and cosine are periodic functions, there are infinitely many associated angles for every value from . Therefore, in order to invert sine and cosine, their definition range is restricted to the interval for sine and to for cosine. Sine and cosine are strictly monotonic at these intervals and are therefore reversible. ${\displaystyle \arcsin }$ ${\displaystyle \operatorname {asin} }$ ${\displaystyle \arccos }$ ${\displaystyle \operatorname {acos} }$ ${\displaystyle [-1,1]}$ ${\displaystyle [-1,1]}$ ${\displaystyle [-1,1]}$ ${\displaystyle [-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}]}$ ${\displaystyle [0,\pi ]}$

Together with the arctangent as the inverse function of the (of course also suitably restricted) tangent , the arctangent and arccosine form the core of the class of arctopic functions . Due to the common recently for inverse functions spelling the name spread to calculators spellings start and the classic spelling or displace what may be confused with the reciprocals of the sine and cosine ( cosecant and secant may result). ${\displaystyle f^{-1}}$ ${\displaystyle \sin ^{-1}}$ ${\displaystyle \cos ^{-1}}$ ${\displaystyle \arcsin }$ ${\displaystyle \arccos }$

Definitions

The sine function is -periodic and not injective within a period . Therefore, their domain of definition must be suitably restricted in order to obtain a reversibly unique function. Since there are several possibilities for this restriction, one speaks of branches of the arcsine. Usually the main branch (or main value) ${\displaystyle 2\pi }$

${\displaystyle \arcsin \colon [-1,1]\to \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right],}$

consider the inverse function of the restriction of the sine function to the interval . ${\displaystyle \sin |_{\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}}$ ${\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right],}$

Analogous to the arccosine, the main branch of the arccosine is defined as the inverse function of . This results in with ${\displaystyle \cos |_{[0,\pi ]}}$

${\displaystyle \arccos \colon [-1,1]\to [0,\pi ]}$

also a bijective function. Means

${\displaystyle \arccos(x)+\arcsin(x)={\frac {\pi }{2}}}$

these two functions can be converted into each other.

properties

	Arcsine	Arccosine
Function graph
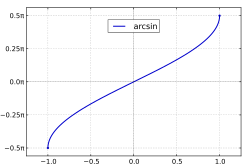
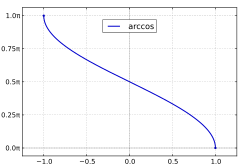
Domain of definition	${\displaystyle x\in [-1,1]}$	${\displaystyle x\in [-1,1]}$
Range of values	${\displaystyle -{\frac {\pi }{2}}\leq f(x)\leq +{\frac {\pi }{2}}}$	${\displaystyle 0\leq f(x)\leq \pi }$
monotony	strictly monotonously increasing	strictly falling monotonously
Symmetries	Odd function: ${\displaystyle \arcsin(-x)=-\arcsin(x)\!}$	Point symmetry too ${\displaystyle \left(x=0\;,\;y={\tfrac {\pi }{2}}\right),}$ ${\displaystyle \arccos(x)=\pi -\arccos(-x)\!}$
Asymptotes	no	no
zeropoint	${\displaystyle x=0\!}$	${\displaystyle x=1\!}$
Jump points	no	no
Poles	no	no
Extremes	Global maximum at , global minimum at ${\displaystyle {\frac {\pi }{2}}}$ ${\displaystyle x=1}$ ${\displaystyle -{\frac {\pi }{2}}}$ ${\displaystyle x=-1}$	Global maximum at , global minimum at ${\displaystyle \pi }$ ${\displaystyle x=-1}$ ${\displaystyle 0}$ ${\displaystyle x=1}$
Turning points	${\displaystyle (x_{W},y_{W})=(0,0)\!}$	${\displaystyle (x_{W},y_{W})=\left(0,{\frac {\pi }{2}}\right)\!}$

Formulas for negative arguments

Due to the symmetry properties:

${\displaystyle \arcsin(-x)=-\arcsin(x)\,}$

${\displaystyle \arccos(-x)=\pi -\arccos(x)\,}$

Series developments

The Taylor series of the arcsine is obtained by applying the binomial series to the derivative, it is given by:

${\displaystyle {\begin{aligned}\arcsin(x)&=\sum _{k=0}^{\infty }{\frac {(2k-1)!!}{(2k)!!}}{\frac {x^{2k+1}}{2k+1}}=\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)}}\\&={x+{\frac {1}{2}}\cdot {\frac {x^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {x^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {x^{7}}{7}}+\cdots }\end{aligned}}}$

The term denotes the dual faculty . ${\displaystyle k!!}$

The arccosine Taylor series is due to the relationship : ${\displaystyle \arccos x={\tfrac {\pi }{2}}-\arcsin x}$

${\displaystyle \arccos(x)={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\frac {(2k-1)!!}{(2k)!!}}{\frac {x^{2k+1}}{2k+1}}={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)}}}$

Both series have the radius of convergence 1.

Integral representations

The integral representations of the arcsine and arcsine are given by:

${\displaystyle \arcsin(x)=\int \limits _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}}$

${\displaystyle \arccos(x)=\int \limits _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}}$

Concatenations with sine and cosine

The following formulas apply to the arc functions:

${\displaystyle \sin(\arccos(x))={\sqrt {1-x^{2}}}}$, because applies to and . ${\displaystyle y=\arccos(x)\!}$ ${\displaystyle y\in \left[0,{\pi }\right]}$ ${\displaystyle \sin(y)={\sqrt {1-\cos ^{2}y}}}$

${\displaystyle \cos(\arcsin(x))={\sqrt {1-x^{2}}}}$, because applies to and . ${\displaystyle y=\arcsin(x)\!}$ ${\displaystyle y\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}$ ${\displaystyle \cos(y)={\sqrt {1-\sin ^{2}y}}}$

${\displaystyle \sin(\arctan(x))={\frac {x}{\sqrt {1+x^{2}}}}}$, because applies to and . ${\displaystyle y=\arctan(x)\!}$ ${\displaystyle y\in \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[}$ ${\displaystyle \sin(y)={\frac {\tan y}{\sqrt {1+\tan ^{2}y}}}}$

${\displaystyle \cos(\arctan(x))={\frac {1}{\sqrt {1+x^{2}}}}}$, because applies to and . ${\displaystyle y=\arctan(x)\!}$ ${\displaystyle y\in \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[}$ ${\displaystyle \cos(y)={\frac {1}{\sqrt {1+\tan ^{2}y}}}}$

Relationship to the arctangent

Of particular importance in older programming languages ​​without implemented arcsine and arcsine functions are the following relationships, which make it possible to calculate the arcsine and arcsine from the arctangent that may have been implemented. Based on the above formulas, the following applies

${\displaystyle \arcsin(x)=\operatorname {sgn}(x)\cdot \arctan \left({\sqrt {\frac {x^{2}}{1-x^{2}}}}\right)}$

${\displaystyle \arccos(x)={\frac {\pi }{2}}-\operatorname {sgn}(x)\cdot \arctan \left({\sqrt {\frac {x^{2}}{1-x^{2}}}}\right)}$

for Defined in this way, these two equations also become correct. Alternatively, you can also ${\displaystyle |x|<1.}$ ${\displaystyle \arctan {\frac {1}{0}}\colon =\lim _{t\to \infty }\arctan t={\frac {\pi }{2}},}$ ${\displaystyle x=\pm 1}$

${\displaystyle \arcsin(x)=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)}$

${\displaystyle \arccos(x)={\frac {\pi }{2}}-2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)}$

use what results from the above by applying the functional equation of the arctangent and applies to. The latter can also be used for ${\displaystyle |x|\leq 1}$ ${\displaystyle -1<x\leq 1}$

${\displaystyle \arccos(x)=2\arctan \left({\sqrt {\frac {1-x}{1+x}}}\right)}$

simplify.

Addition theorems

→ Main article: Addition theorems for arc functions (trigonometry)

The addition theorems for arcsine and arccosine can be obtained with the help of the addition theorems for sine and cosine :

${\displaystyle \arcsin x+\arcsin y=\left\{{\begin{matrix}\arcsin(\sin(\arcsin x+\arcsin y))=\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn }}xy\leq 0{\text{ oder }}x^{2}+y^{2}\leq 1\\\pi -\arcsin(\sin(\arcsin x+\arcsin y))=\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x>0{\text{ und }}y>0{\text{ und }}x^{2}+y^{2}>1\\-\pi -\arcsin(\sin(\arcsin x+\arcsin y))=-\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x<0{\text{ und }}y<0{\text{ und }}x^{2}+y^{2}>1\\\end{matrix}}\right.}$ ${\displaystyle \arccos x+\arccos y=\left\{{\begin{matrix}\arccos(\cos(\arccos x+\arccos y))=\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)&{\text{wenn }}x+y\geq 0\\2\pi -\arccos(\cos(\arccos x+\arccos y))=2\pi -\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)&{\text{wenn }}x+y<0\\\end{matrix}}\right.}$

It follows from this in particular for double function values

${\displaystyle 2\arcsin x=\left\{{\begin{matrix}\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn }}2x^{2}\leq 1\\\pi -\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x>0{\text{ und }}2x^{2}>1\\-\pi -\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn }}x<0{\text{ und }}2x^{2}>1\\\end{matrix}}\right.}$

${\displaystyle 2\arccos x=\left\{{\begin{matrix}\arccos \left(2x^{2}-1\right)&{\text{wenn }}x\geq 0\\2\pi -\arccos \left(2x^{2}-1\right)&{\text{wenn }}x<0\\\end{matrix}}\right.}$

Derivatives

Arcsine

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1}$

Arccosine

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1}$

conversion

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arccos(x)=-{\frac {\mathrm {d} }{\mathrm {d} x}}\arcsin(x)}$

Integrals

Arcsine

${\displaystyle \int \arcsin \left({\frac {x}{a}}\right)\,\mathrm {d} x=x\,\arcsin \left({\frac {x}{a}}\right)+{\sqrt {a^{2}-x^{2}}}+C}$

Arccosine

${\displaystyle \int \arccos \left({\frac {x}{a}}\right)\,\mathrm {d} x=x\,\arccos \left({\frac {x}{a}}\right)-{\sqrt {a^{2}-x^{2}}}+C}$

Complex arguments

${\displaystyle {\begin{aligned}\arcsin(a+b\,\mathrm {i} )=\quad {\frac {\operatorname {sgn^{+}} {a}}{2}}\cdot \arccos &\left({\sqrt {(a^{2}+b^{2}-1)^{2}+4b^{2}}}-(a^{2}+b^{2})\right)\\+\;\mathrm {i} \cdot {\frac {\operatorname {sgn^{+}} {b}}{2}}\cdot \operatorname {arcosh} &\left({\sqrt {(a^{2}+b^{2}-1)^{2}+4b^{2}}}+(a^{2}+b^{2})\right)\end{aligned}}}$   With ${\displaystyle a,b\in \mathbb {R} }$

${\displaystyle \arccos(a+b\,\mathrm {i} )={\frac {\pi }{2}}-\arcsin(a+b\,\mathrm {i} )}$

For the function see Areakosinus hyperbolic , and for the function applies ${\displaystyle \operatorname {arcosh} }$ ${\displaystyle \operatorname {sgn^{+}} \colon \mathbb {R} \to \{-1,1\}}$

${\displaystyle \operatorname {sgn^{+}} (x):=2\cdot \Theta (x)-1={\begin{cases}+1&{\text{für }}x\geq 0\\-1&{\text{für }}x<0\end{cases}}}$

with the Heaviside function . ${\displaystyle \Theta }$

Remarks

Important functional values

See also: Sine and Cosine: Important Function Values

The following table lists the important function values ​​of the two arc functions .

${\displaystyle x}$	${\displaystyle \arcsin(x)}$		${\displaystyle \arccos(x)}$
${\displaystyle 0}$	${\displaystyle 0^{\circ }}$	${\displaystyle 0}$	${\displaystyle 90^{\circ }}$	${\displaystyle {\frac {\pi }{2}}}$
${\displaystyle {\frac {1}{2}}}$	${\displaystyle 30^{\circ }}$	${\displaystyle {\frac {\pi }{6}}}$	${\displaystyle 60^{\circ }}$	${\displaystyle {\frac {\pi }{3}}}$
${\displaystyle {\frac {1}{2}}{\sqrt {2}}}$	${\displaystyle 45^{\circ }}$	${\displaystyle {\frac {\pi }{4}}}$	${\displaystyle 45^{\circ }}$	${\displaystyle {\frac {\pi }{4}}}$
${\displaystyle {\frac {1}{2}}{\sqrt {3}}}$	${\displaystyle 60^{\circ }}$	${\displaystyle {\frac {\pi }{3}}}$	${\displaystyle 30^{\circ }}$	${\displaystyle {\frac {\pi }{6}}}$
${\displaystyle 1}$	${\displaystyle 90^{\circ }}$	${\displaystyle {\frac {\pi }{2}}}$	${\displaystyle 0^{\circ }}$	${\displaystyle 0}$

Other important values ​​are:

${\displaystyle x}$	${\displaystyle \arcsin(x)}$		${\displaystyle \arccos(x)}$
${\displaystyle {\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})}$	${\displaystyle 15^{\circ }}$	${\displaystyle {\tfrac {\pi }{12}}}$	${\displaystyle 75^{\circ }}$	${\displaystyle {\tfrac {5\pi }{12}}}$
${\displaystyle {\tfrac {1}{4}}\left({\sqrt {5}}-1\right)}$	${\displaystyle 18^{\circ }}$	${\displaystyle {\tfrac {\pi }{10}}}$	${\displaystyle 72^{\circ }}$	${\displaystyle {\tfrac {2\pi }{5}}}$
${\displaystyle {\tfrac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}}$	${\displaystyle 36^{\circ }}$	${\displaystyle {\tfrac {\pi }{5}}}$	${\displaystyle 54^{\circ }}$	${\displaystyle {\tfrac {3\pi }{10}}}$
${\displaystyle {\tfrac {1}{4}}\left(1+{\sqrt {5}}\right)}$	${\displaystyle 54^{\circ }}$	${\displaystyle {\tfrac {3\pi }{10}}}$	${\displaystyle 36^{\circ }}$	${\displaystyle {\tfrac {\pi }{5}}}$
${\displaystyle {\tfrac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}}$	${\displaystyle 72^{\circ }}$	${\displaystyle {\tfrac {2\pi }{5}}}$	${\displaystyle 18^{\circ }}$	${\displaystyle {\tfrac {\pi }{10}}}$
${\displaystyle {\tfrac {1}{4}}({\sqrt {6}}+{\sqrt {2}})}$	${\displaystyle 75^{\circ }}$	${\displaystyle {\tfrac {5\pi }{12}}}$	${\displaystyle 15^{\circ }}$	${\displaystyle {\tfrac {\pi }{12}}}$

Continued fraction representation of the arcsine

In 1948, HS Wall found the following representation as a continued fraction for the arcsine :

${\displaystyle \arcsin(x)={\frac {x{\sqrt {1-x^{2}}}}{1-{\cfrac {1\cdot 2x^{2}}{3-{\cfrac {1\cdot 2x^{2}}{5-{\cfrac {3\cdot 4x^{2}}{7-{\cfrac {3\cdot 4x^{2}}{9-{\cfrac {5\cdot 6x^{2}}{11-\ldots }}}}}}}}}}}}}$

Complex function

The arcsine and arcsine can also be expressed by the main branch of the complex logarithm :

${\displaystyle \arcsin z=-\mathrm {i} \,\ln \left(\mathrm {i} z+{\sqrt {1-z^{2}}}\right)}$

${\displaystyle \arccos z=-\mathrm {i} \,\ln \left(z+\mathrm {i} {\sqrt {1-z^{2}}}\right)}$

These two formulas can be derived as follows:

For : ${\displaystyle \arcsin z}$

${\displaystyle {\begin{aligned}\sin(x)={\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}\\{\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}=z\\\mathrm {e} ^{\mathrm {i} x}-{\frac {1}{\mathrm {e} ^{\mathrm {i} x}}}=2z\mathrm {i} \\(\mathrm {e} ^{\mathrm {i} x})^{2}-1=2z\mathrm {i} \mathrm {e} ^{\mathrm {i} x}\\(\mathrm {e} ^{\mathrm {i} x})^{2}-2z\mathrm {i} \mathrm {e} ^{\mathrm {i} x}-1=0\\\mathrm {e} ^{\mathrm {i} x}=-{\frac {-2z\mathrm {i} }{2}}\pm {\sqrt {\left({\frac {-2z\mathrm {i} }{2}}\right)^{2}-(-1)}}\\\mathrm {e} ^{\mathrm {i} x}=z\mathrm {i} \pm {\sqrt {1-z^{2}}}\\\mathrm {i} x=\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\x={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})}{\mathrm {i} }}\\x={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\,\mathrm {i} }{\mathrm {i} ^{2}}}\\x={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\,\mathrm {i} }{-1}}\\x=-\mathrm {i} \,\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\\arcsin z=-\mathrm {i} \,\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\\end{aligned}}}$

For : ${\displaystyle \arccos z}$

${\displaystyle {\begin{aligned}\cos(x)={\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}\\{\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}=z\\\mathrm {e} ^{\mathrm {i} x}+{\frac {1}{\mathrm {e} ^{\mathrm {i} x}}}=2z\\(\mathrm {e} ^{\mathrm {i} x})^{2}+1=2z\mathrm {e} ^{\mathrm {i} x}\\(\mathrm {e} ^{\mathrm {i} x})^{2}-2z\mathrm {e} ^{\mathrm {i} x}+1=0\\\mathrm {e} ^{\mathrm {i} x}=-{\frac {-2z}{2}}\pm {\sqrt {\left({\frac {-2z}{2}}\right)^{2}-1)}}\\\mathrm {e} ^{\mathrm {i} x}=z\pm {\sqrt {z^{2}-1}}\\\mathrm {i} x=\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\x={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})}{\mathrm {i} }}\\x={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\,\mathrm {i} }{\mathrm {i} ^{2}}}\\x={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\,\mathrm {i} }{-1}}\\x=-\mathrm {i} \,\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\\arccos z=-\mathrm {i} \,\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\\end{aligned}}}$

See also

• Trigonometry formula collection
• Trigonometric functions

literature

• Ilja Bronstein, Konstantin Semendjajew: Pocket book of mathematics . BG Teubner, Stuttgart 1991. ISBN 3-87144-492-8 .

Individual evidence

1. ↑ Eric W. Weisstein : Inverse Trigonometric Functions . In: MathWorld (English).
2. ↑ George Hoever: Higher Mathematics compact . Springer Spectrum, Berlin Heidelberg 2014, ISBN 978-3-662-43994-4 ( limited preview in Google book search).