Point of discontinuity

Function with point of discontinuity

{\ displaystyle x_ {0}}

In analysis , a branch of mathematics, a function is referred to as discontinuous wherever it is not continuous within its domain of definition . A point at which a function is discontinuous is therefore also referred to as a discontinuity point or discontinuity .

The article Continuous function explains when a function is continuous and when it is discontinuous. Different types ( classes ) of discontinuities are presented in this article . Only real-valued functions on a real interval are considered.

definition

As mentioned, a function defined on the real interval is called discontinuous at that point if it is not continuous there. One also speaks of a function discontinuous on a set if the function is discontinuous at every point . ${\ displaystyle [a, b]}$ ${\ displaystyle f \ colon [a, b] \ rightarrow \ mathbb {R}}$ ${\ displaystyle x_ {0} \ in [a, b]}$ ${\ displaystyle I \ subset [a, b]}$ ${\ displaystyle x \ in I}$

Classifications of discontinuities

Different “types” of discontinuities are distinguished. For this purpose, the one-sided limit values are considered:

For a real interval and consider the limit value on the left ${\ displaystyle [a, b]}$ ${\ displaystyle f \ colon [a, b] \ rightarrow \ mathbb {R}}$ ${\ displaystyle x_ {0} \ in (a, b)}$

{\ displaystyle f (x_ {0} ^ {-}): = \ lim _ {x \ rightarrow x_ {0} ^ {-}} f (x)}

and the right hand limit

{\ displaystyle f (x_ {0} ^ {+}): = \ lim _ {x \ rightarrow x_ {0} ^ {+}} f (x).}

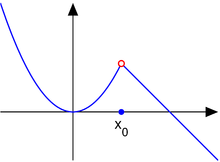
Now is continuous at if both limits exist and are equal to the function value at the point: . Otherwise it is discontinuous at the point. The following cases are possible: ${\ displaystyle f}$ ${\ displaystyle x_ {0}}$ ${\ displaystyle f (x_ {0} ^ {-}) = f (x_ {0} ^ {+}) = f (x_ {0})}$ ${\ displaystyle f}$

A point of discontinuity is called liftable if the limit values and exist, are finite and equal. Such a discontinuity can be removed, more precisely: the function is continuous at that point .

{\ displaystyle f (x_ {0} ^ {-})}

{\ displaystyle f (x_ {0} ^ {+})}

{\ displaystyle g (x): = {\ begin {cases} f (x), & x \ neq x_ {0}, \\ f (x_ {0} ^ {-}), & x = x_ {0} \ end {cases}}}

{\ displaystyle x_ {0}}

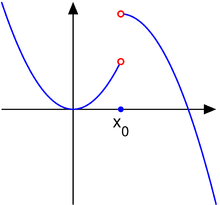
If both limit values exist and are finite but not equal, one speaks of a jump point and defines the jump . The jump can of course also be defined for liftable discontinuities, it is then . (The notation of the jump bracket is also used for the jump at this point :) If all one-sided limit values exist in the entire definition range of a function and if these are finite, the function is called continuous jump or control function. ${\ displaystyle s: = f (x_ {0} ^ {+}) - f (x_ {0} ^ {-})}$ ${\ displaystyle s = 0}$ ${\ displaystyle x_ {0}}$ ${\ displaystyle [[f (x_ {0})]]: = s}$

A pole (or pole ) is called a discontinuity at which and exist, but one or both limit values only in an improper sense, i.e. i.e., they accept the values or (see also pole position ). ${\ displaystyle f (x_ {0} ^ {-})}$ ${\ displaystyle f (x_ {0} ^ {+})}$ ${\ displaystyle + \ infty}$ ${\ displaystyle - \ infty}$

Finally, there is also the possibility that at least one of the limit values neither actually nor improperly exists.

Heaviside function

Cases 1 and 2 are also referred to as discontinuities of the first kind ; Cases 3 and 4, respectively, as discontinuities of the second kind , or sometimes also as essential discontinuities .

Representation of points of discontinuity in function graphs

If there is a left and / or right-hand limit value for the point of discontinuity, these are shown in the graph of the function as small circles, which are filled in if the limit value in question is also a function value at the point in question, otherwise they remain empty (or in simplified representations sometimes be omitted entirely).

Examples

Example 1: liftable discontinuity

Example 1: The function

{\ displaystyle f (x) = {\ begin {cases} x ^ {2} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ 2-x & {\ mbox {for}} x> 1 \ end {cases}}}

has a liftable discontinuity at this point. ${\ displaystyle x_ {0} = 1}$

Example 2: jump point

Example 2: The function

{\ displaystyle f (x) = {\ begin {cases} x ^ {2} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ 2- (x- 1) ^ {2} & {\ mbox {for}} x> 1 \ end {cases}}}

has a jump point at this point with a jump of 1. ${\ displaystyle x_ {0} = 1}$

Example 3: discontinuity of the second kind

Example 3: The function

{\ displaystyle f (x) = {\ begin {cases} \ sin {\ frac {5} {x-1}} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ {\ frac {0.1} {x-1}} & {\ mbox {for}} x> 1 \ end {cases}}}

has a discontinuity of the second kind at this point . The left-hand limit value does not exist (neither actually nor improperly), the right-hand limit value is . ${\ displaystyle x_ {0} = 1}$ ${\ displaystyle + \ infty}$

Example 4: The Thoma's function is discontinuous on the rational numbers and continuous on the irrational numbers. The Dirichlet function is discontinuous over its entire domain.

Discontinuities of monotonic functions

If the function is monotonic on the real interval , the one-sided limit values and exist for all . Therefore, such monotonic functions have no points of discontinuity of the second kind. The set of points of discontinuity of the first kind of such monotonic functions is at most countable, but can be very close to the definition range. ${\ displaystyle f \ colon [a, b] \ rightarrow \ mathbb {R}}$ ${\ displaystyle [a, b]}$ ${\ displaystyle x \ in (a, b)}$ ${\ displaystyle f (x ^ {-})}$ ${\ displaystyle f (x ^ {+})}$

literature

Walter Rudin: Analysis . 4th edition. Oldenbourg Verlag, Munich 2009, ISBN 978-3-486-58730-2 , 4th continuity: points of discontinuity, p. 109–110 (English: Principles of mathematical analysis . Translated by Martin Lorenz and Christian Euler).

Harro Heuser: Textbook of Analysis . Part 1. 17th edition. Vieweg and Teubner, Wiesbaden 2009, ISBN 978-3-8348-0777-9 , 39. Unilateral limit values, p. 239 .

Kurt Endl and Wolfgang Luh: Analysis I . An integrated representation. 9th edition. Aula-Verlag, Wiesbaden 1989, ISBN 3-89104-498-4 , 2.12 Limit values of functions, p. 126 .

Ilja N. Bronstein et al .: Taschenbuch der Mathematik . 7th edition. Verlag Harri Deutsch, Frankfurt aM 2008, ISBN 978-3-8171-2017-8 , 2.1.5.2 Definition of continuity and 2.1.5.3 Frequently occurring types of discontinuities, p. 59 .

Hans-Jochen Bartsch: Pocket book of mathematical formulas . 20th edition. Fachbuchverlag Leipzig, Munich 2004, ISBN 3-446-22891-8 , 7.4.3 Continuity of a function, p. 371 .

Individual evidence

^ Walter Rudin: Analysis . 4th edition. Theorem 4.29, p. 109 .
^ Walter Rudin: Analysis . 4th edition. Theorem 4.30, p. 110 .
↑ Kurt Endl and Wolfgang Luh: Analysis I . An integrated representation. 9th edition. Theorem 2.13.2.
↑ Harro Heuser: Textbook of Analysis . Part 1. 17th edition. Theorem 39.5, p. 239 .
^ Walter Rudin: Analysis . 4th edition. Remark 4.31, p. 110 (For every countable subset E from the domain of definition, whether dense or not, a monotonic function can be constructed that is discontinuous on E and otherwise continuous.).

[1] Walter Rudin: Analysis . 4th edition. Theorem 4.29, p. 109 .

[2] Walter Rudin: Analysis . 4th edition. Theorem 4.30, p. 110 .

[3] Kurt Endl and Wolfgang Luh: Analysis I . An integrated representation. 9th edition. Theorem 2.13.2.

[4] Harro Heuser: Textbook of Analysis . Part 1. 17th edition. Theorem 39.5, p. 239 .

[5] Walter Rudin: Analysis . 4th edition. Remark 4.31, p. 110 (For every countable subset E from the domain of definition, whether dense or not, a monotonic function can be constructed that is discontinuous on E and otherwise continuous.).