Thoma's function

Graph of the Thomas function on (0,1)

The Thoma's function , named after the German mathematician Carl Johannes Thomae (1840–1921), is a mathematical function that is discontinuous on the rational numbers and continuous on the irrational numbers . It is related to the Dirichlet function and, like this, has no practical meaning, but serves as an example for continuity and other mathematical topics.

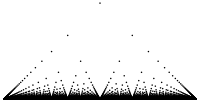
Other terms based on the graph are ruler function , raindrop function , popcorn function (after popcorn in the pan) or star over Babylon after John Horton Conway .

definition

The Thoma's function is defined as a real-valued function by: ${\displaystyle f\colon [0,1]\rightarrow \mathbb {R} }$

${\displaystyle f(x)=\left\{{\begin{array}{ll}{\frac {1}{q}}\ ,&{\text{wenn }}x>0{\text{ und }}x={\frac {p}{q}}{\text{ rational mit }}\operatorname {ggT} (p,q)=1\,\\0\ ,&{\text{wenn }}x{\text{ irrational ist,}}\\1\ ,&{\text{wenn }}x=0.\\\end{array}}\right.}$

The Thoma's function is a simple example of a function whose set of discontinuities is complicated. More precisely: is continuous on all irrational numbers in [0,1] and discontinuous on all rational numbers in this interval. ${\displaystyle f}$

Roughly speaking, this can be shown as follows: If is irrational and is close to , then is either irrational or a rational number with a large denominator. In both cases is close . If, on the other hand, is rational and a sequence of irrational numbers in (0,1) that converges to, then which does not converge to. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle f(x)=0}$ ${\displaystyle x}$ ${\displaystyle (y_{n})_{n\in \mathbb {N} }}$ ${\displaystyle x}$ ${\displaystyle f(y_{n})\equiv 0}$ ${\displaystyle f(x)\neq 0}$

Related question

Conversely, however, there is no function that is continuous on the rational numbers and discontinuous on the irrational numbers, because the set of points of discontinuity is always a -set ( Young's theorem ), while from Baier's category theorem it follows that the set of irrational numbers no amount is. ${\displaystyle F_{\sigma }}$ ${\displaystyle F_{\sigma }}$

Sets of discontinuities

With the help of a variant of the Thomean function, one can show that any subset of the actually occurs as a set of discontinuities of a function . For if there is a countable union of closed sets , then one posits ${\displaystyle F_{\sigma }}$ ${\displaystyle A}$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle f_{A}\colon \mathbb {R} ^{d}\rightarrow \mathbb {R} }$ ${\displaystyle \textstyle A=\bigcup _{n=1}^{\infty }F_{n}}$ ${\displaystyle F_{n}}$

${\displaystyle f_{A}(x):=\left\{{\begin{array}{ll}{\frac {1}{n}}\ ,&{\text{falls }}x\in A\cap \mathbb {Q} ^{d}{\text{ und }}n{\text{ minimal, so dass }}x\in F_{n},\\-{\frac {1}{n}}\ ,&{\text{falls }}x\in A\setminus \mathbb {Q} ^{d}{\text{ und }}n{\text{ minimal, so dass}}\ x\in F_{n}\ ,\\0\ ,&{\text{falls }}x\notin A.\\\end{array}}\right.}$

Using an argument similar to that of the Thomean function, one sees that the set of discontinuities is of. ${\displaystyle A}$ ${\displaystyle f_{A}}$

literature

• Robert G. Bartle, Donald R. Sherbert: Introduction to Real Analysis . 3. Edition. Wiley, 1999, ISBN 978-0-471-32148-4 , Example 5.1.6 (h).
• Stephen Abbot: Understanding Analysis . Springer-Verlag, Berlin 2001, ISBN 0-387-95060-5 .

Individual evidence

1. ↑ "... the so-called 'ruler function', a simple but provocative example that appeared in a work by Johannes Karl Thomae ... The graph suggests the vertical markings on a ruler - hence the name." Quoted from William Dunham: The Calculus Gallery : Masterpieces from Newton to Lebesgue . Princeton University Press, 2004, ISBN 978-0-691-09565-3 , Chapter 10.