quadrant

The four quadrants of a coordinate system

A quadrant ( Latin quadrans 'quarter') is a section of a plane delimited by two coordinate axes , whereby the points on the delimiting axes usually do not belong to any quadrant.

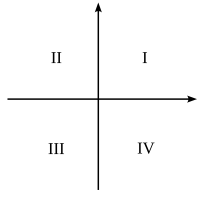
According to the usual conventions, the first quadrant is drawn at the top right. In a Cartesian coordinate system , the four quadrants are denoted counterclockwise with I, II, III, IV and 1, 2, 3, 4, respectively. A point in the first quadrant then has positive coordinates.

quadrant	I.	II	III	IV
x coordinate	pos.	neg.	neg.	pos.
y coordinate	pos.	pos.	neg.	neg.

However, other classifications are also used.

Relation to trigonometry

In trigonometry , the signs of the trigonometric functions sine , cosine , tangent or cotangent - and their 360 ° periods - depend on the quadrant into which the angle extends:

Quadrant table
	${\ displaystyle \ alpha}$	${\ displaystyle \ sin {} \ alpha}$	${\ displaystyle \ cos {} \ alpha}$	${\ displaystyle \ tan \ alpha}$	${\ displaystyle \ cot \ alpha}$
1st quadrant	0-90 °	+	+	+	+
2nd quadrant	90-180 °	+	-	-	-
3rd quadrant	180-270 °	-	-	+	+
4th quadrant	270-360 °	-	+	-	-

Each of the trigonometric functions has the same sign in two quadrants. Hence the archetype of the value of a trigonometric function, e.g. B. the sine , ambiguous.

For example , an angle α in the 3rd or 4th quadrant, i.e. π <α <2 · π or 180 ° <α <360 °, can result. ${\ displaystyle \ sin \ alpha <0}$

A quadrant table - or a corresponding query in a PC program - is always necessary in geodesy or navigation in order to calculate the direction (the azimuth , the course ) from the coordinates of two points .

If the boundaries between the quadrants and their edges are also important, the following table results (formulated in rad ):

Quadrant table
	${\ displaystyle \ alpha}$	${\ displaystyle \ sin {} \ alpha}$	${\ displaystyle \ cos {} \ alpha}$	${\ displaystyle \ tan \ alpha}$	${\ displaystyle \ cot \ alpha}$
+ x-axis	0	0	1	0	${\ displaystyle \ pm \ infty}$
1st quadrant	(0, π / 2)	+	+	+	+
+ y-axis	π / 2	1	0	${\ displaystyle \ pm \ infty}$	0
2nd quadrant	(π / 2, π)	+	-	-	-
−x axis	π	0	−1	0	${\ displaystyle \ pm \ infty}$
3rd quadrant	(π, 3π / 2)	-	-	+	+
-Y axis	3π / 2	−1	0	${\ displaystyle \ pm \ infty}$	0
4th quadrant	(3π / 2, 2π)	-	+	-	-

Dentistry

Quadrant numbering in the FDI tooth scheme

In dentistry , a quadrant is one half of the jaw. The dentition thus consists of four quadrants. In the FDI tooth scheme , the quadrant number is placed in front of the code number of the tooth. The quadrants are numbered counterclockwise from the patient's point of view, starting with the upper jaw on the right.

literature

Hans-Jochen Bartsch: Pocket book of mathematical formulas for engineers and natural scientists . 22nd edition. Carl Hanser Verlag GmbH & Co. KG, 2011, ISBN 978-3-446-42785-3 .
Werner Tiki coastal maker, Heinz Partoll, Irmgard Wagner: Mathe macchiato . 1st edition. Pearson Studium, Munich 2003, ISBN 3-8273-7061-2 .

Web links

Eric W. Weisstein : Quadrant . In: MathWorld (English).
Thomas Foregger, Mathprof: Quadrant . In: PlanetMath . (English)

Individual evidence

↑ Ekkehard Finkeissen: Dental Decision Making . BoD - Books on Demand, August 2002, ISBN 978-3-8311-4198-2 , p. 251.

[Finkeissen2002-1] Ekkehard Finkeissen: Dental Decision Making . BoD - Books on Demand, August 2002, ISBN 978-3-8311-4198-2 , p. 251.