Euler's equations (gyro theory)
The Euler gyroscopic equations or ambiguous Euler equations are equations of motion for the rotation of a rigid body . They are the components of the swirl theorem written down for the rigid body in its main axis system and represent the most important basic equation of the gyroscopic theory.
If the body is subjected to a torque , gyroscopic effects develop , which try to bring the rotation into line with the forced rotation. The gyroscopic effects are the summed torques of the Euler forces and centrifugal forces at all mass points of the body. The moment and the gyroscopic effects are in dynamic equilibrium , which is expressed by the gyro equations:
There are each for
- the external torques ,
- the main moments of inertia ,
- the angular momentum ,
- the angular velocities and
- the angular accelerations
in the main axis system. Occasionally, the associated vector equation is also used
given with the inertia tensor as Euler's gyroscopic equation. Here “·” forms the vector transformation , “×” the cross product and the relative time derivative in the main axis system.
The torques, main moments of inertia and angular momentum are calculated with a reference point for which the center of mass or an unaccelerated support point resting in an inertial system is suitable, see the principle of twist on a rigid body .
The first summands on the right-hand side, consisting of the angular accelerations and changes in angular momentum, result from the gyroscopic effects of the Euler forces and the other terms, which are quadratic in the angular velocities and angular momentum, take into account the gyroscopic effects of the centrifugal forces. If the movement is known, then these equations can be used to calculate the moments that must be introduced at the reference point so that the body executes the specified movement.
The gyro equations were drawn up by Leonhard Euler in 1750 and later further developed into the theorem of swirl .
Special cases
Euler-Poisson equations
The Euler-Poisson equations are the specific gyroscopic equations for heavy gyros where the external moment comes from gravity . The classic gyro theory is almost exclusively devoted to the heavy gyro with support point and a lot of effort has been put into finding exact solutions. A listing of some of these solutions can be found in the main article.
Spherical top
A spherical top is a top with three identical main moments of inertia Θ, so that the gyro equations are then based on
to reduce. With the spherical top, the angular acceleration is parallel to the applied moment. With the spherical top, the centrifugal forces in the body are always in mechanical equilibrium . A comparison with the equations of motion for a translational motion shows that the spherical top is the exact analog of the mass point in a rotational motion .
Level movements
In the case of a plane movement around a main axis of inertia , for example the 3-axis, rotations and moments around the 1 and 2 axes are omitted, and the equations are reduced to
where φ is the angle of rotation around the 3-axis.
Solutions of the gyro equations for plane movements
In the plane case, the gyroscopic equations can often be solved analytically, for which the two following cases are examples.
Kick of a billiard ball
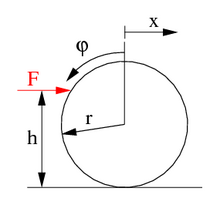
Parallel to the table top, a billiard ball with radius r , mass m and mass moment of inertia Θ should be pushed so that it does not slip over the table, see Fig. 1. The question arises as to the height h above the table at which the force F is introduced must, so that no friction force on the table is necessary for the slip-free rolling.
The eccentric horizontal force acting on the ball develops a moment M = - (hr) F around the center of mass, which the ball according to the gyroscopic equation
set in rotation. The moment is negative because it acts against the counting direction of the angle of rotation φ . In addition, the force accelerates the ball according to the law " force equals mass times acceleration ":
The acceleration is parallel to the table in the direction of the force. The condition for slip-free rolling
closes the system of equations for the three unknowns h, φ and x . This is calculated
In the case of a massive, homogeneous sphere, the mass moment of inertia is Θ = 2 ⁄ 5 mr² and thus
where d = 2r is the diameter of the sphere.
A wheel rolling down an incline
In a plane movement, a wheel with radius r , mass m and mass moment of inertia Θ rolls down a plane inclined at angle α under the influence of a gravitational acceleration g , see Fig. 2.Because the wheel also moves in a translatory manner, its mass also goes into the Acceleration on. However, the acceleration increases when the mass moment of inertia decreases.
Due to the slip-free rolling, a frictional force R arises at the contact point of the wheel, which sets the wheel in rotation, because it corresponds to a moment M = - r R around the center of mass. The moment is negative because it works against the counting direction of the angle of rotation φ . So the gyro equation reads in the plane case:
The component F of the weight mg acting on the wheel downhill has the size F = mg sin ( α ). It is opposed by the frictional force, so that according to Newton's second law :
where the acceleration of the wheel counting down the slope and sin is the sine function . The condition for slip-free rolling closes the equation system for the three unknowns R , φ and x and it results
A block sliding down a slope without friction experiences an acceleration that is greater than that of the wheel, because a part of the potential energy is converted into rotational energy, which is then missing for translation.
Example: centrifugal pendulum
A remarkable application of Euler's gyroscopic equations is the "pearl on a rotating circular ring in the gravitational field", the conical or centrifugal pendulum , because it has surprising properties. In the words of the gyro theory, it is a heavy gyroscope , which is held in a point and in which the rotation around the pendulum axis is prevented by external moments and the precession speed is kept constant. More complex properties occur with any position of the center of mass and with an initial alignment of the main axes. Simplifications result with the center of mass on the 1-axis and permanently horizontal 3-axis of the main axis system.
kinematics
The usual definitions of angles and angular velocities in gyro theory are adopted. In particular, the z component becomes the 2-axis
required for a horizontal 3-axis (ϑ ≡ 90 °), which is identical to the 2-component of the unit vector , which points vertically upwards. The functions sin and cos form the sine and cosine .
The angular velocities are under the local conditions:
The angle ϑ is invariable if it initially has no time derivative and does not experience any acceleration over the long term.
kinetics
The 1 or pendulum axis bears the center of mass at a distance s > 0 from the fixed point , whose weight mg thus exerts a moment of gravity on the pendulum. In addition to this gravity moment, external moments M 1,2 act in the 1- or 2-direction of the main axis system in order to suppress angular accelerations of ϑ and μ . The gyro equations in 1 and 2 directions only serve to determine these moments, which are of no interest here. It is noteworthy, however, that these torques cause a temporal change in the vertical angular momentum, which is always constant with heavy gyroscopes .
The pendulum can rotate freely around the horizontal 3-direction and the moment of gravity in this direction is - mgsn 2 = - mgs cos ( φ ), see kinematics above and Euler-Poisson equations . This gives the third of the gyro equations
the equation of motion
|
|
|
(*)
|
|
|
Here A, B and C are the main moments of inertia about the 1-, 2- and 3-axis respectively.
Equilibrium positions
In equilibrium the angular acceleration vanishes in (*) :
- .
In contrast to the Lagrange top left to its own devices, precession with a horizontal axis ( φ = 0) is not possible. In the absence of self-rotation, there is no gyroscopic effect that could compensate for the gravity. The equilibrium with a vertical 1-axis ( φ = ± 90 °) is accessible to all gyroscopes - including the spherical gyroscope , which only finds equilibrium there. At A ≠ B the equilibrium positions result from
If A - B has the same sign as sin ( φ ), the term in the square brackets can become zero. To do this must
be fulfilled. The pendulum must exceed a critical speed of rotation μ c so that this equilibrium position exists away from the vertical. With the flattened top, the 1-axis points upwards in equilibrium (is A> B and sin ( φ )> 0) and with the stretched top downwards ( A <B and sin ( φ ) <0).
Analogous to the symmetric top is here and below the pendulum flattened called if A> B , and stretched when B> A .
Energy consideration
Multiplication of the equation of motion (*) with enables time integration:
The integration constant E is the energy of the pendulum in the rotating system:
- the first term contributes the rotational energy around the 3-axis,
- the second term is the centrifugal potential of precession and
- the third term stands for the potential energy in the earth's gravitational field.
The energy and its derivatives (·) 'with respect to φ result from the abbreviation to
For the straight top, B> A and z <0 and for the flattened top, B <A and z > 0. Stability exists in an energy minimum where E ' = 0 and E "> 0. The energy is stationary in equilibrium positions : at sin ( φ ) = z or cos ( φ ) = 0, where sin ( φ ) = -1 or sin ( φ ) = +1:
- Equilibrium position with sin ( φ ) = z
- Here E "= (AB) μ² (z²-1) . This movement is stable with the straight top if z 2 <1, i.e. always, and with the flattened top , if z 2 > 1, i.e. never.
- Hanging pendulum sin ( φ ) = -1
- Here E "= (AB) μ² (1 + z) . The bottom dead center is stable with the flattened top if z > -1, i.e. always, and with the extended top , if z <-1, i.e. | μ | < μ c With increasing μ , the straight pendulum passes through a subcritical pitch fork bifurcation at μ = μ c , where the stable position at bottom dead center becomes unstable and two stable equilibrium positions with sin ( φ ) = z arise. In contrast to this, the vertically hanging Lagrangian Gyroscope always stable, see there.
- Upright pendulum sin ( φ ) = +1
- Here is E "= (AB) μ² (1-z) The top dead center is stable when stretched roundabout when. Z > 1, that never, and when the flattened, z <1 or | microns > | microns c increasing case. μ the flattened pendulum passes through a supercritical pitch fork bifurcation at μ = μ c , where the unstable position becomes stable at top dead center and two new unstable equilibrium positions arise with sin ( φ ) = z .
Vibrations
The equation (*) can be linearized around equilibrium positions φ 0 , where z = sin ( φ 0 ). For this purpose, φ = φ 0 + δ with a constant φ 0 and a small deviation δ is assumed. The spin
develops with the addition theorems and sin ( δ ) ≈ δ , cos ( δ ) ≈ 1 to the oscillation equation
- With
In the elongated top, B> A and the "reset coefficient" in front of δ is always positive, which is why the elongated top can perform small oscillations around equilibrium positions. In the flattened top, the reset coefficient is negative because A> B. Therefore, the flattened top cannot oscillate about equilibrium positions away from the vertical, which is consistent with the results from the energy analysis .
See also
- Poinsot construction : graphic description of the moment-free movement.
- Physical pendulum
Individual evidence
- ↑ Grammel (1920), p. 70.
-
↑ In the tensor algebra can be dispensed Parentheses:
- ↑ Clifford Truesdell : The Development of the Swirl Theorem . In: Society for Applied Mathematics and Mechanics (ed.): Journal for Applied Mathematics and Mechanics (= Issue 4/5 ). tape 44 , April 1964, p. 149 - 158 , doi : 10.1002 / zamm.19640440402 ( wiley.com ).
- ↑ Magnus (1971), p. 109.
- ↑ a b c d P. Eckelt: Theoretical Mechanics. (PDF) Institute for Theoretical Physics at the Westfälische Wilhelms-Universität Münster, 2000, pp. 11 to 13 , accessed on July 16, 2016 (see also the sources given there).
- ^ Arnold (1988), pp. 95 f.
- ↑ Grammel (1920), p. 111.
literature
- Herbert Goldstein, Charles P. Poole, Jr, John L. Safko: Classical Mechanics . 3. Edition. Wiley-VCH, Weinheim 2006, ISBN 3-527-40589-5 .
- K. Magnus: Top . Theory and applications. Springer, Berlin / Heidelberg / New York 1971, ISBN 3-540-05198-8 , pp. 49 .
-
R. Grammel : The top . Its theory and its applications. Vieweg Verlag, Braunschweig 1920, DNB 451641280 , p. 45 ( archive.org - "swing" means angular momentum, " rotational shock " about the torque and "rotational force" rotational energy). or R. Grammel: The top. Its theory and its applications . 2. revised Edition. 1: The theory of the top. Springer, Berlin / Göttingen / Heidelberg 1950, DNB 451641299 , p.
23 . - VI Arnol'd (В. И. Арнолъд): Mathematical methods of classical mechanics . Birkhäuser Verlag, Basel 1988, ISBN 978-3-0348-6670-5 , p. 95 f ., doi : 10.1007 / 978-3-0348-6669-9 ( limited preview in Google Book Search [accessed on February 14, 2018] Russian: Математическе методы классическоя механики . Moscow 1979. Translated by Prof. Dr. Peter Möbius , TU Dresden). or V. I. Arnol'd: Mathematical Methods of Classical Mechanics . 2nd Edition. Springer, New-York / Berlin / Heidelberg / London / Paris / Tokyo 1989, ISBN 3-540-96890-3 , pp.
150 . - Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point . Springer Verlag, Berlin, Heidelberg 1965, ISBN 3-642-88414-8 , p. 6 , doi : 10.1007 / 978-3-642-88412-2 (English, limited preview in Google Book Search [accessed December 27, 2019]).


























![{\ displaystyle {\ ddot {\ varphi}} = {\ frac {1} {C}} [(AB) \ mu ^ {2} \ sin (\ varphi) -mgs] \ cos (\ varphi)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac6a875910ba56cacc71c07aa8f6e222f3aab88f)
![{\ displaystyle C {\ ddot {\ varphi}} = [(AB) \ mu ^ {2} \ sin (\ varphi) -mgs] \ cos (\ varphi) = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aac4cbf9af5d24c074fd68d290694919c056f54a)
![{\ displaystyle \ left [\ sin (\ varphi) - {\ frac {mgs} {(AB) \ mu ^ {2}}} \ right] \ cos (\ varphi) = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83095d1b57c7b7ebbc070c662b4f8be312946c31)




![{\ displaystyle {\ begin {aligned} E = & {\ frac {C} {2}} {\ dot {\ varphi}} ^ {2} + (BA) \ mu ^ {2} {\ bigg (} { \ frac {\ sin ^ {2} (\ varphi)} {2}} - z \ sin (\ varphi) {\ bigg)} \\ E '= & (BA) \ mu ^ {2} [\ sin ( \ varphi) -z] \ cos (\ varphi) \\ E '' = & (BA) \ mu ^ {2} [1 + z \ sin (\ varphi) -2 \ sin ^ {2} (\ varphi) ] \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d88a545716ab6d569c3728ae85aa6dd573729f70)



