Gyro theory

from Wikipedia, the free encyclopedia

Fig. 1: Regular precession of a symmetrical top

The gyro theory deals with rotating bodies, in which displacements in space and changes in shape are of minor importance.

Bodies, to which this description applies, are collectively referred to in theory as gyroscopes and contain such different objects as spinning tops , long projectiles or the earth . The gyroscopic movements are equally interesting for mathematics, physics and engineering - thus for theory and practice. The aim of the theory is to put applications like the ones below on a safe footing.

Leonhard Euler founded the (analytical) gyro theory in 1750 by setting up the gyro equations that are named after him today . The gyroscopic equations are the counterpart to Newton's second law, force equals mass times acceleration, for rotating rigid bodies and are comparable fundamental to physics.

The classical gyroscopic theory is almost exclusively dedicated to the heavy gyro , which, as the animation shows, with its inertia in a peculiar way resists falling over due to its weight. Up to the beginning of the 21st century , movements that could be analytically represented were found only in a few cases and the question of the solvability of the gyroscopic equations in the vast majority of gyroscopic movements remains open. The modern gyro theory is dedicated to the general properties of the dynamic system. In real gyroscopic phenomena, friction effects are essential, with which, for example, the erecting of the game top can be explained.

The gyro theory is used in railway engineering ( sinusoidal movement ), the spin stabilization of ships ( ship gyro ), spacecraft and inertial navigation systems as well as in astronomy and ballistics .

history

The scientific treatment of tops began with JA Segner (1704 - 1777), who also correctly recognized the importance of friction for the erection of the top axis. Leonhard Euler developed a theory of precession in 1736 and the gyro equations in 1750, which he was able to solve in 1758 for the force-free Euler gyro or at least trace back to elliptic integrals . From now on it was possible to derive knowledge from solutions of the equations, which however turned out to be an extremely persistent "gyro problem".

Unlike Newton's second law, which celebrated spectacular successes in celestial mechanics, a solution of the gyro equations was only possible with the Euler gyro and only 38 years later (1788) with the heavy symmetrical gyro with a fixed point by Joseph-Louis Lagrange . In 1829 Carl Gustav Jacob Jacobi published the theory of the elliptical and theta functions , with which the gyro equations can be solved. Jacobi demonstrated this at the Euler gyro, and in 1849 he recommended several times to tackle the problem with these functions. In the meantime (1834) Louis Poinsot contributed his illustrative geometric interpretation of the gyroscopic movements and Siméon Denis Poisson published his kinematic equations (1838).

Despite the promising approach with theta functions and competitions by the Prussian and Russian Academy of Sciences in the 1850s, the "mathematical mermaid ", as the gyro problem in Germany has meanwhile been dubbed due to the aesthetics of the object and the basic equations as well as its mathematical inaccessibility, turned out to be. as extremely inaccessible. Sofia Kovalevskaya discovered in 1888 the last case that could be solved by theta functions, the heavy, symmetrical, inhomogeneous Kovalevskaya top , with which the analytical top theory came to a certain conclusion. The standard works by Klein and Sommerfeld (written 1896–1910), Richard Grammel (1920, 1950) or Kurt Magnus (1971) can still be used at the beginning of the 21st century. Proof of this is that the first work was still translated into English 100 years after its publication.

AM Lyapunov proved in 1894 that the three cases of Euler, Lagrange and Kowalewskaja are the only ones in which the solution of the equations of motion is a unique function of time under any initial conditions, and É. Husson showed in 1905 that these gyroscopes are the only cases that can be solved by algebraic #integrals of motion . Around 1900 mathematicians found some integrable special cases , but the question of the solvability of the vast majority of gyroscopic motions remains open into the 21st century.

Although the classical gyroscopic theory dealt mainly with the rigid body with a fixed point, gyro-like phenomena on rotating chains, deformable bodies - especially the earth - or liquids were investigated. Space travel added new problems, such as

  • self-excitation (moments applied in the body-fixed system) for the purpose of stabilization and position control, see stabilization (space travel) ,
  • the movements of bodies with variable masses,
  • the movements of rigid bodies filled with fluids,
  • the rotary movements in a central gravitational field or
  • influencing translational and rotational movements.

From the middle of the 20th century, computer hardware and software, and with them numerical simulation , developed to such an extent that the equations of motion can be calculated with any initial conditions and with any desired accuracy. The analytical solutions now lost their previously justified, central importance and the theory turned to the non-integrable cases. Analytical and geometric methods emerged for their investigation, which were repeatedly motivated by the Kovalevskaya gyroscope, which occupied science throughout the 20th century. The investigation methods of integrable cases were transferred to non-integrable dynamic systems at the beginning of the 21st century.

Properties of the tops and their movements

The gyroscopic theory understands a top to be a rigid body of any shape that executes rotating movements. This idealizing model for real gyroscopes enables their behavior to be recorded with simpler mathematical tools. The classical gyro theory concentrated on the heavy gyro , which is held in an inertial system in one of its points in such a way that it can somehow turn around this point. This requirement is only a small restriction, because every rigid body movement can be broken down into rotation and translation, and if the latter is (approximately) uniform , it does not play a role for the circular movement. By fixing a point in the three-shift drop degrees of freedom away, leaving only the three rotational degrees of freedom of the gyro, see #Bezugssysteme and Euler angles .

The speed of the rotary movement is insignificant in the gyro theory. The relatively slowly revolving "earth gyroscope" is subject to the gyroscopic laws just like a technical gyroscope rotating at 60,000 rpm , but the laws of these so-called fast gyroscopes are extremely simplified .

Fig. 2: Form of movement of a symmetrical, prolate, force-free top

The movements of the force-free top are called nutation in top theory and the externally excited precession . However, these terms are not uniform. Arnold, for example, calls the periodic change in the inclination of the figure axis relative to the plumb line in the Lagrange top nutation and the azimuthal rotation precession.

The axis of rotation of a gyroscope is not fixed to the body, so it can move relative to the gyroscope and sweeps over the corridor pole cone or pole cone for short. At the same time, the axis of rotation also moves in space, creating a surface, the locking pole or track cone. The leading curve of the cone is the end point of the angular velocity vector, which sometimes fluctuates chaotically, only seldom assumes one state twice and generates any shaped track cone and pole cone . If the top has a fixed point, then the tips of the cones are located at this fixed point, and the movement of the top can be interpreted as a non-slip rolling of the pole cone fixed in the body on the spatially fixed track cone. In regular precession as in the symmetrical Euler gyro, the cones are circular cones and the movement through the cones is particularly clear, see Fig. 2.

Fig. 3: Spoked wheel precessing horizontally in a circle (along the red ellipse R) (bold black)

The force-free top follows the law of conservation of energy in the absence of external influences . Such conserved quantities are of great interest in gyroscopic theory and are called #integrals of motion . Closely related to the game top is the Lagrange top , on which paradoxical top effects stand out:

  • the precession with a horizontal figure axis , see Fig. 3, and
  • the erection of the top against gravity, as with the standing top .

With the Kovalevskaya gyroscope , the movement functions are mathematically demanding and almost all of its movements change their stability behavior if they are faster or slower. The German mathematician Wilhelm Hess discovered the loxodromic pendulum in 1890 , the center of gravity of which moves like a spherical pendulum under gyro-specific gravitational acceleration, see Fig. 4.

Fig. 4: Simulated movement of a Hess pendulum with center of gravity axis and angular momentum plane (black), main axes (blue), angular momentum (red) and angular velocity (green)

Each top can perform permanent rotation around a body-fixed vertical axis. Also pseudo regular Precessions possible if the angular momentum is large aligned near a symmetry axis and. The movement resembles the regular precession , in which the top rotates evenly around a fixed axis and another fixed to the body, as shown in Fig. 1 , and the two axes form a constant angle. In the pseudo-regular precession but occur with the eye almost imperceptible, small, overlapping, cycloid similar oscillations of the axis of rotation according to one of astronomy borrowed word also nutations be mentioned. A compilation of some cases in which exact solutions of the equations of motion were successful up to the beginning of the 21st century can be found in the Euler-Poisson equations .

The energy surface on which the angular velocity travels can be described analytically for all gyroscopes and it turns out that the surface can branch out in unstable relative equilibria , for example if the vertically positioned gyro is unstable. In such branch points the energy surface changes its properties ( topology ), which can be represented analytically and is of interest in terms of gyroscopic theory.

Angular momentum and rotational inertia

The momentum of a mass point , its inertia in the momentary movement, is given physically by its momentum , which is the product of the mass and the speed. The momentum of gyroscopes, their inertia in the momentary rotation, is given by their angular momentum , which is a vector quantity with direction and length. The greater the angular momentum, the more difficult it is to keep the top from its momentary rotation.

Fig. 5: Inertial ellipsoid (blue network) and main axes (blue arrows) of a top (not shown)

The angular momentum of a mass point rotating with a top is given by its distance from the axis of rotation and its momentum, which increases with the speed, which increases in the top with the distance to the axis of rotation. Thus the angular momentum of a mass point is proportional to the square of its distance to the axis of rotation. The product of the mass and the square of the distance to the axis of rotation is the moment of inertia of the mass point and the summation over all mass points of the gyroscope provides its moment of inertia about the respective axis.

The rotational inertia properties when rotating around a reference point on the axis of rotation can be clearly shown for a top by its ellipsoid of inertia , see Fig. 5. The distance between the reference point and the point of intersection of the axis of rotation with the ellipsoid of inertia determines the moment of inertia J about the axis. The semi-axes of the ellipsoid of inertia are the main axes and their relative lengths are related to the main moments of inertia of the top, which are physical quantities that characterize the top .

The axis of rotation does not have to be fixed, but can move in space and relative to the top, whereby its moment of inertia can change with the direction of the axis. In contrast to speed and momentum, the relationship between rotational speed and angular momentum is time-dependent and, moreover, both quantities do not have to be parallel.

A characteristic dimension of the gyro can be used to scale the lengths and a main moment of inertia to scale the time or energy, which is why two gyros with similar ellipsoids and comparable positions of the center of mass and the reference point revolve in a similar way with the same initial conditions .

Swirl rate

The dynamics of the gyro can be formulated with the angular momentum similar to the dynamics of the mass point:

Principle of inertia
The force-free top moves in such a way that its angular momentum remains constant in terms of magnitude and direction (just like a force-free mass point moves uniformly).
Swirl rate (principle of action)
Under the influence of torques , the gyroscope moves in such a way that the rate of change of the angular momentum vector in terms of direction and magnitude is equal to the applied moment (just like the acceleration of the mass point in the direction of an applied force).

The analogies between rotation and translational motion stop where the typical gyroscopic motion begins. Because while momentum and speed are always parallel and proportional to each other during translation, this does not apply to angular momentum and rotational speed in the cases that are interesting from a gyroscopic theory point of view. Is an initially resting centrifugal by a rotational shock displaced about an axis in rotation, then it must not revolve around this axis. With constant angular momentum, the angular velocity does not have to be constant and vice versa, which is supported by the Dschanibekow effect and the Euler gyroscope . In general:

  • With constant angular momentum, the axis of rotation changes continuously with free movement and the top wobbles or "eels".
  • If the axis of rotation is held, then the angular momentum changes continuously, for which the brackets of the axis of rotation bring in the necessary moments and remove the gyroscopic effects .
Fig. 6: On the rule of parallelism in the same direction

The principle of swirl is the most important physical law in gyro theory and is usually reflected in the same-directional parallelism , see Fig. 6 .: If a torque M is applied to the gyro, then the gyro tries to rotate, expressed by the angular momentum L , the To align the direction of rotation of the moment in the same direction, which is indicated in blue in the picture.

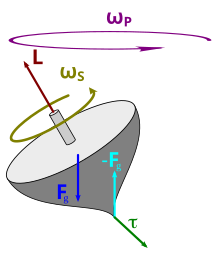
Fig. 7: Forces made up of weight F g and oppositely equal contact force - F g as well as the corresponding moment τ for the regularly precessing top.

This principle explains many properties of the gyroscopic movements. For example, if a force acts on a top with a fixed point, then a counterforce is created at the fixed point and with it a force couple that exerts a moment perpendicular to the plane of the force couple, see Fig. 7. In its direction - always perpendicular to the force - the top deviates . However, this only applies to the angular momentum and only in the case of a fast gyroscope also to the axis of rotation or possibly the main axis around which the gyro rotates. The precession with a horizontal axis of rotation as in Fig. 3 can also be clearly explained with the rule applied to the gyroscopic effect of the axial angular momentum .

Gyroscopic effect

The most striking feature of gyroscopes is that of the gyroscopic effect or the gyroscopic effect, which becomes noticeable as an amazing expression of force when you try to move the axis of rotation of a top into a new position. The gyroscopic effect manifests itself as a resistance that can go far beyond what is known from a resting body.

According to the rule of parallelism in the same direction, the gyroscopic effect tries to bring the axis of its own rotation in direction and orientation to coincide with the axis of the forced rotation. It is a d'Alembertian inertial force and as such a moment of equal magnitude opposite to an attacking moment: moment and gyroscopic effect are balanced out (are in dynamic equilibrium .)

The gyroscopic effect is equal to the sum of the moments exerted in the body by the Euler and centrifugal forces . The Euler forces are an expression of the inertia against angular accelerations , and the centrifugal forces arise from the inertia of the mass points against changes in the direction of their movement. In the directions perpendicular to an attacking moment, the gyroscopic effects of the Euler and centrifugal forces neutralize each other and are there in dynamic equilibrium. The Euler forces are an expression of the angular accelerations that are caused by the centrifugal forces in the top. Conversely, the angular accelerations lead to a change in the axis of rotation and the rotational speed, which influences the centrifugal forces. The result of this dynamic interplay is the aforementioned tumbling and "egg" of the force-free top.

The centrifugal effects are observed curve gyros , edge runners technically exploited and the swirl stabilization.

Twist stabilization

Fig. 8: Flywheel to explain the spin stabilization

One of the technically most valuable properties of gyroscopes is the ability to use them to stabilize bodies in their spatial alignment. As mentioned above, this is used in ships, spacecraft and projectiles.

The twist stabilization can be seen in the simple flywheel in Fig. 8, whereby the figure axis (initially in the y-direction) is free so that it can change its direction at will. A constant moment M z acts on this otherwise force-free flywheel for a short time in the z-direction, which causes the flywheel to rotate about z. This rotation is noticeable differently on the stationary and rotating flywheels:

  1. If the flywheel is at rest, the moment causes it to rotate around z. After the moment has ceased to act, the flywheel continues to rotate around z, the rotation angle ψ of the figure axis around z increases monotonically and is unlimited. The angular velocity and the angular momentum have only one component and they point in the z-direction. The angle of inclination ϑ between the figure axis and the moment axis z remains unchanged.
  2. If the flywheel rotates sufficiently quickly around the figure axis at the beginning, a different picture emerges. The moment leads to a linear increase in the angular momentum in the z-direction, but because this component is vectorially added to the initial angular momentum in the y-direction (assumed to be much larger), i.e. the angular momentum continues to be oriented primarily in the y-direction , and angular momentum and angular velocity enclose an acute angle (see energy ellipsoid ), the flywheel continues to rotate mainly around the y-axis. As a result, the angle of rotation ψ of the figure axis remains limited by z. According to the rule of parallelism in the same direction, the top tries to adjust its rotation to the attacking moment, whereby the angle ϑ decreases.

The reason for the small influence of the moment on the rotation of the rotating flywheel around z is the inertial forces that build up gyroscopic effects. If the axis of rotation is somehow held by bearings, they neutralize these gyroscopic effects and the inertial forces cannot develop their potential. Twist stabilization only occurs in gyroscopes that have full freedom of movement in three degrees of freedom of rotation. But even then, twist stabilization does not always succeed, as William Thomson, 1st Baron Kelvin and Peter Guthrie Tait were able to show.

Integrals of motion

In the centrifugal theory in the rotation of a gyroscope immutable physical quantities integrals , sometimes first integrals called English first integrals . These are of outstanding importance because they enable the solution of the gyro equations or at least, like the Jellett integral in the game top , characterize the movements.

With the force-free Euler gyro , the angular momentum is constant and its spatially fixed components and its amount are integrals with the gyro. If the gravitational field is conservative , like that of the earth, the gyroscopic motion obeys the law of conservation of energy , which is why the total energy is then an integral. In the case of a heavy top , the moment of vertical gravity has no component in the perpendicular direction and thus the angular momentum in this direction is an integral. However, the integrals, such as the Kovalevskaya constant , do not always have a clear meaning.

With the heavy gyro there are always three first integrals (the Euler-Poisson equations ) with six unknowns. If a fourth integral is found, then a fifth integral can be constructed with the method of the last multiplier devised by Carl Gustav Jacob Jacobi , with which the equations of motion are solved. Because one of the six unknowns takes on the role of the independent variable, since the time does not appear explicitly in the equations.

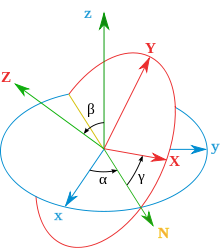
Reference systems and Euler angles

Fig. 9: Euler's basic system (green) indicates the axes around which the Euler angles ψ = α , ϑ = β and φ = γ rotate.

Two reference systems are mainly used in gyro theory :

In the inertial system (blue in Fig. 9), in which the reference point rests and the top rotates, the Euler angles are defined, which indicate the orientation of the main axes of the top in space. The timing of the angles determines the movement function of the top. In a fixed-space system, the mass moments of inertia can vary over time about non-fixed axes.

In the co-rotating, body-fixed reference system (red), the equations of motion are particularly easy to formulate, because there the moments of inertia are constant over time. Inertial forces occurring here must be taken into account in the equations of motion . These are the Euler force and the centrifugal force . Coriolis forces do not occur here because the rigid body does not have any movement of its mass points relative to the body.

In gyro theory, the basis vectors are expressed in the space-fixed reference system with Euler's angles in the standard x-convention (z, x ′, z ″). The angle ψ is the precession angle , ϑ the angle of inclination and φ determines the rotation of the top. Denote the unit vectors ê x, y, z the space-fixed standard base (blue in Fig. 9) and ê X, Y, Z  =  ê 1,2,3 the rotating with the body, motion base (red), then read the co-moving base unit vectors with regard to the fixed base:

The vector

marks the node axis (yellow N in the picture). The angular velocity its components and the vectors hang over

together. Often the components ω 1,2,3 in the main axis system are also referred to as p , q and r and occasionally the angles ψ and φ change the meaning.

At sin ϑ  = 0 a singularity occurs because then, because of cos ϑ  = ± 1, the angles ψ and φ in the basis vectors according to the addition theorems only occur as a combination ition ± φ and thus different angles can lead to the same basis.

Footnotes

  1. ^ Grammel (1920), p. 2, Grammel (1950), p. 3.
  2. ^ Grammel (1920), p. V, Grammel (1950), p. III, Magnus (1971), p. 1.
  3. ^ Grammel (1920), p. 3.
  4. ↑ Gashenenko and Richter (2003), pp. 2527, 2532.
  5. ↑ Felix Klein , Conr. Müller: Encyclopedia of the Mathematical Sciences with inclusion of its applications . Mechanics. Ed .: Academies of Sciences in Göttingen , Leipzig, Munich and Vienna. Fourth volume, 1st part volume. BG Teubner, 1908, ISBN 978-3-663-16021-2 , p. 546 , doi : 10.1007 / 978-3-663-16021-2 ( limited preview in the Google book search [accessed on January 24, 2020] see also wikisource }).
  6. ↑ Ludwig Darmstaedter (Ed.): Handbook for the history of natural sciences and technology . Springer-Verlag, Berlin, Heidelberg 1908, p. 209 ( wikimedia.org [PDF; accessed January 19, 2020]).
  7. ↑ Clifford Truesdell : The Development of the Swirl Theorem . In: Society for Applied Mathematics and Mechanics (ed.): Journal for Applied Mathematics and Mechanics (=  Issue 4/5 ). tape 44 , April 1964, p. 154 , doi : 10.1002 / zamm.19640440402 ( wiley.com ).
  8. ↑ Leonhard Euler : About the movement of the rotation of rigid bodies around a variable axis . In: Royal Prussian Academy of Sciences in Berlin (ed.): Mémoires de l'Académie des Sciences de Berlin . tape 14 . Petersburg 1758, p. 173 and 190 . (French, archive.org [accessed on January 11, 2020] Original title: Du mouvement de rotation des corps solides autour d'un ax variable .).
  9. ^ Joseph-Louis Lagrange : Mécanique Analytique . Tome Second. Corucier, Paris 1815, p.  265 f . (French, archive.org [accessed August 20, 2017]). or Joseph-Louis Lagrange: Analytical Mechanics . Vandenhoeck and Ruprecht, Göttingen 1797 ( archive.org [accessed on August 20, 2017] German translation by Friedrich Murhard).
  10. ↑ ink man and Hawig (1993) 123rd
  11. ^ Siméon Denis Poisson : Traité de Méchanique . 3. Edition. 1 to 6. JG Garnier, Brussels 1838 (French, archive.org [accessed on November 3, 2019]).
  12. ↑ Tuschmann and Hawig (1993), p. 123., Audin (2008), p. 91.
  13. ↑ ink man and Hawig (1993), S. 119th
  14. ↑ see literature and F. Klein , A. Sommerfeld : The Theory of the Top. Volume I . Introduction to the Kinematics and Kinetics of the Top. Volume I. Birkhäuser, Basel, Boston 2008, ISBN 978-0-8176-4720-9 , pp. vii ff ., doi : 10.1007 / 978-0-8176-4721-6 (English, springer.com - original title: About the theory of the gyro . Translated by RJ Nagem, G. Sandri, there is a foreword by the translator with a historical outline here online as a PDF file .).
  15. ↑ Édouard Husson: Research on algebraic integrals in the motion of a heavy body around a fixed point . In: Annales de la faculté des sciences de Toulouse 2 e série . 1906, p. 73–152 , doi : 10.5802 / afst.232 (French, numdam.org [PDF; accessed on March 7, 2018] Original title: Recherche des intégrales algébriques dans le mouvement d'un solid pesant autour d'un point fixe . On page 74, a first attempt at evidence by Roger Liouville in 1897 is revealed to be incorrect). , see also Audin (2008), p. 106.
  16. ↑ Leimanis (1965), p. 53 ff.
  17. ↑ Magnus (1971), p. 129.
  18. ↑ a b Gashenenko and Richter (2003), p. 2525.
  19. ↑ K. Magnus : Kreiselprobleme / Gyrodynamics . Symposion Celerina, August 20-23, 1962 / Symposion Celerina, August 20-23, 1962. Ed .: Hans Ziegler. Springer Verlag, Berlin a. a. 1963, ISBN 978-3-662-12200-6 , pp. 7 , doi : 10.1007 / 978-3-662-12200-6 ( limited preview in Google Book search).
  20. ↑ Magnus (1971), p. 109.
  21. ↑ Gashenenko and Richter (2003), pp. 2532 f.
  22. ↑ Magnus (1971), p. 1.
  23. ↑ Grammel (1920), p. 3, Grammel (1950), p. 2, Tuschmann and Hawig (1993), p. 121.
  24. ↑ Magnus (1971), pp. 2f.
  25. ↑ Magnus (1971), p. 119
  26. ↑ Duden│Precession. Duden online, accessed on November 5, 2017 . and Duden│Nutation. Duden online, accessed on March 8, 2018 .
  27. ↑ Vladimir I. Arnol'd: Mathematical Methods of Classical Mechanics . Springer-Verlag, Basel 1988, ISBN 978-3-0348-6670-5 , p. 159 , doi : 10.1007 / 978-3-0348-6669-9 ( limited preview in Google Book Search [accessed February 14, 2018] Russian: Математическе методы классическоя механики . Moscow 1979. Translated by Prof. Dr. Peter Möbius. TU Dresden).
  28. ↑ Magnus (1971), p. 27.
  29. ↑ Kuypers (2016), p. 215
  30. ^ EF Autenrieth , Max Ensslin: Technical Mechanics: A textbook of statics and dynamics for engineers . Springer-Verlag, Berlin 1922, ISBN 978-3-642-98876-9 ( limited preview in Google book search [accessed November 5, 2017]).
  31. ↑ Magnus (1971), p. 108.
  32. ↑ a b Gashenenko and Richter (2003), p. 2526 f.
  33. ↑ Klein and Sommerfeld (1910), p. 762.
  34. ↑ Magnus (1971), p. 2 and p. 47, Grammel (1920), p. 43.
  35. ↑ Grammel (1920), p. 18.
  36. ↑ Klein and Sommerfeld (1910), p. 764.
  37. ↑ Grammel (1920), pp. 59 + 62.
  38. ^ Grammel (1920), p. 3
  39. ↑ Grammel (1920), p. 70.
  40. ↑ Klein and Sommerfeld (1910), p. 767 f.
  41. ↑ Grammel (1950), p. 261 f.
  42. ^ Carl Gustav Jacob Jacobi : Lectures on dynamics . Ed .: A. Clebsch. G. Reimer Verlag, Berlin 1884, p. 73 ff . ( archive.org [accessed March 7, 2020]).
  43. ↑ Leimanis (1965), p. 10.
  44. ↑ Grammel (1920), p. 51.

literature

Web links