Coriolis force

A hurricane created by the Coriolis force

The Coriolis force [kɔrjoˈliːskraft] is an inertial force . In a rotating reference system , for example on a rotating disk, it can be determined that a body does not move uniformly in a straight line according to Newton's second law , but is deflected perpendicular to the direction of movement. This deflection is caused by the Coriolis acceleration and interpreted as the effect of a laterally acting force, the Coriolis force. Likewise, in the case of a linear movement in the rotating reference system, one finds that a force must be built up perpendicular to the direction of movement, but that this does not lead to any change in speed. This force is opposite to the Coriolis force and has the same amount. In contrast to the two other inertial forces in rotating reference systems, the centrifugal force and the Euler force , the Coriolis force only acts on bodies that move in the rotating reference system.

Since the Coriolis acceleration is perpendicular to the direction of movement, the amount of speed in the rotating reference system remains constant, only its direction changes. As Coriolis every phenomenon is called, caused by the Coriolis force.

On the rotating earth , the influence of the Coriolis force can be clearly seen in large-scale phenomena, such as B. in meteorology with the direction of rotation of the wind fields around high and low pressure areas and with the formation of earth-encompassing wind systems such as the trade winds and the jet stream . In oceanography , the Coriolis force has a major impact on ocean currents . The widespread thesis that it is also responsible for the direction of rotation of the vortex in the bathtub and in the sink, however, does not apply.

This inertial force was first derived by Pierre-Simon Laplace in 1775 . But it is named after Gaspard Gustave de Coriolis , who dealt with it in detail in a publication published in 1835.

introduction

Movement of a body outward from the center of a rotating disc without friction; above: in the stationary frame of reference the body moves uniformly in a straight line ; below: in the co-rotating reference system (disk) the body moves on a spiral curved path .

In a well-known demonstration experiment on the Coriolis effect, a ball is made to roll over a rotating disk from the center. After bumping into it, the ball rolls in a straight line when viewed from outside the disk; it moves uniformly because of its inertia . In the real experiment, the disk takes it along a little in the direction of rotation. If the ball is thrown instead of rolled, this effect can be avoided. On the other hand, on the disk, i.e. in the rotating reference system, the ball is deflected in the opposite direction to the disk rotation and describes a clearly curved path. The lateral deviation, seen from the outside the path of the red point in the animation, is explained in the rotating reference system with the tangential component of the Coriolis acceleration, which depends on the radial speed.

In general, the Coriolis acceleration is calculated using the formula ${\displaystyle {\vec {a}}_{C}}$

${\displaystyle {\vec {a}}_{\mathrm {C} }=-2\,{\vec {\omega }}\times {\vec {v}}'}$.

This article follows this definition of the sign that is commonly used in physics today. In the formula denote the vectorial angular velocity of the rotation of the reference system, the amount of which indicates how fast the reference system rotates and whose direction is the axis of rotation. The speed at which the body moves in the rotating frame of reference is denoted by. ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {v}}'}$

In analogy to Newton's second law , a force proportional to the acceleration is assumed in physics, the Coriolis force, which is the product of the mass of the body and the Coriolis acceleration : ${\displaystyle m}$

${\displaystyle {\vec {F}}_{\mathrm {C} }=m\,{\vec {a}}_{\mathrm {C} }=-2\,m\,{\vec {\omega }}\times {\vec {v}}'}$

This force is an inertial force and only occurs in the rotating frame of reference. However, since there is no physical cause for this force and no other body on which it acts back, it is also referred to as a fictitious force or apparent force. The combination of both quantities can be expressed by the cross product with the symbol . The three vectors form a legal system . The so-called “ three-finger rule ” can be used for its didactic illustration . ${\displaystyle \times }$

The direction of the resulting vector is both perpendicular to the current direction of movement and to the axis of rotation of the system. The Coriolis force therefore always lies in a plane perpendicular to the axis of rotation; it is zero for movements parallel to the axis of rotation. If one looks in the rotating reference system against the direction of the angular velocity, i. H. perpendicular to the plane, the body is always deflected to the right. ${\displaystyle {\vec {F}}_{\mathrm {C} }}$

Centrifugal and Coriolis forces influence the movements on the "devil's wheel"

Another attempt can be seen occasionally on rides , in which the principle of inertia can be experienced. People should walk on a rotating disc. Do they move e.g. B. rectilinear radial to the center, forces are required for this, since the movement from the outside is not a state of rest or uniform movement. External force and inertial forces are oppositely equal; they form a dynamic equilibrium . Since the circumferential speed of the disc is getting smaller and smaller on the way in, the rotor has to apply a force against the direction of rotation. This force is the opposite of the Coriolis force. The Coriolis force can also be interpreted here as inertial resistance. Since the centrifugal force and the Coriolis force are perpendicular to each other under these conditions, they could be distinguished by people. The pane could also be covered and not allow a view to the outside. The appearance of external forces during a uniform movement is therefore also the proof that one is not in an inertial system .

Clear derivation

The following considerations, which make the phenomenon more or less understandable on the basis of finite intervals in time and space, give an exact justification of the Coriolis force in the limit of infinitesimally small intervals.

Coriolis acceleration with radial movement away from the axis of rotation

Deflection by the Coriolis force during radial movement

A person stands on a disc at a distance from the center (red point A), and further out at a distance there is a pole (red point 1). The person throws a body towards the stake at speed . If the disc were to rest, the body would fly along the red line and hit the stake after time . Unless the person is aware of the rotation (or its effect on free movement), they will always expect that straight-line movement in the direction in which they threw the body away. ${\displaystyle r}$ ${\displaystyle r+\Delta r}$ ${\displaystyle v}$ ${\displaystyle \Delta t=\Delta r/v}$

While the thrown body is in the air, the disc rotates through the angle , where is the angular velocity. The person moving along covers the distance on the arc (blue arrow) and is then at the red point B. The post covers a greater distance on its arc because it is further out. He is then at red point 2. The difference between the two lengths of the stake and person is ${\displaystyle \Delta \varphi =\omega \,\Delta t}$ ${\displaystyle \omega }$ ${\displaystyle r\Delta \varphi }$ ${\displaystyle (r+\Delta r)\Delta \varphi }$

${\displaystyle \Delta s=\Delta r\Delta \varphi }$.

The thrower expects the thrown body at the place where the pole is now, i.e. at point 2 at the end of the dotted straight red line. For him, however, the body flew past the post along the curved dotted red line at a distance . ${\displaystyle \Delta s}$

This can be explained by a “resting” observer who stands next to the turntable and does not have to take into account any inertial forces caused by the accelerated reference system: The body initially moved with the throwing person on the rotating disk. So at the moment of throwing it has a tangential speed of rotation and, perpendicular to it, also receives the radial throwing speed . After being released, it moves in a straight line at the speed resulting from and (red-blue arrow). It covers the distance in the radial direction, the distance in the tangential direction and therefore reaches the point marked with the green cross. The distance in the tangential direction is just as long as the distance that the person covers on his or her arc during this, because . When the body arrives at the green cross, it still lacks the path to the post  . ${\displaystyle v_{t}=\omega \,r}$ ${\displaystyle v}$ ${\displaystyle v}$ ${\displaystyle v_{t}}$ ${\displaystyle v\Delta t}$ ${\displaystyle v_{t}\,\Delta t}$ ${\displaystyle v_{t}\,\Delta t=r\,\omega \Delta t=r\,\Delta \varphi }$ ${\displaystyle \Delta s}$

Now grows quadratically over time, because the following applies: ${\displaystyle \Delta s}$

${\displaystyle \Delta s=\Delta \varphi \Delta r=\omega \,\Delta t\,v\,\Delta t=\omega \,v\,(\Delta t)^{2}}$.

For the person rotating with it, it looks like an evenly accelerated movement . For them applies at a given acceleration ${\displaystyle a}$

${\displaystyle \Delta s={\frac {1}{2}}\,a\,(\Delta t)^{2}}$.

Thus, the person rotating with the body can see the deviation of the body from the intended direction due to the acceleration

${\displaystyle a_{C}=2\,w\,v}$

to explain. This is the Coriolis acceleration, which in this case is only directed tangentially.

This derivation is not entirely conclusive insofar as the pieces on the arcs were treated like straight lines. In the limit of infinitesimally small distances, this is exact. Therefore, the formula thus obtained is valid.

Coriolis acceleration with circular movement around the axis of rotation

See also : Centripetal acceleration # Simple derivation

Quite generally, an acceleration in the direction of the center point is required to maintain a circular movement at a distance at any speed . If a rotating body has the speed in the inertial system, the result is the centripetal acceleration , which occurs with all circular movements and is caused by the centripetal force. ${\displaystyle r}$ ${\displaystyle {\tilde {v}}}$ ${\displaystyle {\tilde {a}}_{\text{r}}={\tilde {v}}^{2}/r}$ ${\displaystyle {\tilde {v}}=v}$ ${\displaystyle a_{\text{r}}=v^{2}/r}$

If a body moves with the speed (relative speed) in a reference system that executes a rotational movement with the angular speed , then the speed of the body from the inertial system is the sum of the speed of rotation and the relative speed : ${\displaystyle v'}$ ${\displaystyle \omega }$ ${\displaystyle v_{\text{Umlauf}}=\omega \cdot r}$ ${\displaystyle v'}$

${\displaystyle v=v_{\text{Umlauf}}+v'}$.

For the centripetal acceleration of the body it follows:

${\displaystyle a_{\text{r}}={\frac {(v_{\text{Umlauf}}+v')^{2}}{r}}={\frac {v_{\text{Umlauf}}^{2}}{r}}+{\frac {v{'}^{2}}{r}}+2{\frac {v_{\text{Umlauf}}\,v'}{r}}=a_{\text{Zp}}+a'_{r}+2\,\omega \,v'}$.

This is the centripetal acceleration that belongs to the movement under consideration in the stationary reference system. It is made up of three terms. The first is the centripetal acceleration experienced by a body connected to the frame of reference. This is followed by the relative acceleration and a term that is opposite to the Coriolis acceleration. The example shows that this division depends on the chosen reference system and is therefore arbitrary.

Resolved according to the radial acceleration in the rotating reference system :

${\displaystyle a'_{\text{r}}=a_{\text{r}}-a_{\text{Zp}}-2\,\omega \,v'=a_{\text{r}}+a_{\text{Zf}}+a_{\text{C}}}$.

The second term is the centrifugal acceleration. The opposite is the same as the centripetal acceleration of a body that is connected to the reference system. The third term is the Coriolis acceleration.

No Coriolis acceleration when moving parallel to the axis of rotation

A movement of a body parallel to the axis of rotation does not produce a Coriolis force, because no additional forces are necessary to explain it. For example, consider the case that on a horizontal turntable at a certain distance from the center there is a vertical climbing pole, on which a person slides down. For them, the centrifugal force remains constant because the distance from the axis of rotation remains constant. The holding force required to maintain the constant distance, which is applied by the rod, then also remains constant. For a stationary observer, the downward movement parallel to the axis is superimposed with a circular movement around the axis, together that is a screw movement. The centripetal force required for the circular movement around the axis is exerted by the rod and is independent of the height and vertical movement of the body.

It seems different at first when you jump vertically on the turntable or throw an object up parallel to the axis of rotation. When falling, the starting point is not reached again - neither in relation to the disc nor in relation to the solid ground. But even with this deflection, no Coriolis force appears, but only the temporary lack of holding force or centripetal force, which in the previous example was exerted all the time by the rod. The body is then accelerated outwards for the rotating observer by the centrifugal force, for the stationary observer it simply continues to move in a straight line at its initial momentary speed. Both descriptions lead to the same result.

Derivation from the basic kinematic equations

Derivation by transformation from an inertial system

See also : Accelerated reference system # kinematics

For the derivation of the Coriolis force in the context of Newtonian mechanics, consider a reference system that is located in an inertial system and rotates with constant angular velocity . The coordinate origin of the system is firmly anchored in the inertial system, so apart from the rotation there is no relative movement. ${\displaystyle K'}$ ${\displaystyle K}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle K'}$

According to Newton's second law , the product of mass and acceleration in the inertial system is equal to the external force  : ${\displaystyle m}$ ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {F}}}$

${\displaystyle m{\vec {a}}={\vec {F}}}$

If you want to set up an analog equation in a rotating frame of reference, the quantities of motion in the inertial frame must be expressed by quantities that can be observed in the rotating frame of reference . These are the position vector , the relative speed and the relative acceleration . The speed in the inertial system is made up of the relative speed and the rotational speed from the rotational movement. This results from the time derivative of the position vector , therefore: ${\displaystyle K'}$ ${\displaystyle {\vec {r}}'}$ ${\displaystyle {\vec {v}}'}$ ${\displaystyle {\vec {a}}'}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle {\vec {\omega }}\times {\vec {r}}'}$ ${\displaystyle {\vec {r}}={\vec {r}}'}$

${\displaystyle {\vec {v}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\vec {v}}'+{\vec {\omega }}\times {\vec {r}}'\,.}$

Since in general the following applies for the complete derivative of a vector in K ': ${\displaystyle {\vec {x}}'}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {x}}'={\frac {\mathrm {d'} }{\mathrm {d} t}}{\vec {x}}'+\omega \times {\vec {x}}'}$,

the acceleration in the inertial system results in the same way as a time derivative of the speed . ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {v}}}$

${\displaystyle {\vec {a}}=\underbrace {{\vec {a}}'+{\vec {\omega }}\times {\vec {v}}'} +\underbrace {{\vec {\omega }}\times ({\vec {v}}'+{\vec {\omega }}\times {\vec {r}}')} }$

The terms above the curly brackets are the derivatives of the two summands relative velocity and velocity. Multiplying, combining and resolving according to the relative acceleration in the rotating system results in: ${\displaystyle {\vec {a}}'}$

${\displaystyle {\vec {a}}'={\vec {a}}-{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')-2{\vec {\omega }}\times {\vec {v}}'\,.}$

If the equation is multiplied by the mass and, according to Newton's second law, equals the external force , the equation of motion in the rotating reference system is obtained: ${\displaystyle m{\vec {a}}}$ ${\displaystyle {\vec {F}}}$

${\displaystyle m{\vec {a}}'={\vec {F}}-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')-2m{\vec {\omega }}\times {\vec {v}}'\,.}$

This equation contains the external force, the centrifugal force and, as the last term, the Coriolis force : ${\displaystyle {\vec {F}}_{\mathrm {C} }}$

${\displaystyle {\vec {F}}_{\mathrm {C} }=-2m\,{\vec {\omega }}\times {\vec {v}}'}$

If the external force and the inertial forces are combined to form the force effective in the rotating frame of reference , external force and inertial forces can no longer be formally distinguished in the equation of motion: ${\displaystyle {\vec {F}}\,'}$

${\displaystyle m{\vec {a}}'={\vec {F}}\,'}$

Derivation with the Lagrange formalism

In the Lagrange formalism , the Lagrange function is the difference between kinetic energy and potential energy . Neglecting a potential is ${\displaystyle L}$

${\displaystyle L={\tfrac {1}{2}}m{\vec {v}}^{2}={\tfrac {1}{2}}m({\vec {v}}'+{\vec {\omega }}\times {\vec {r}}')^{2}\,.}$

According to the Euler-Lagrange equations ,

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\vec {v}}}}-{\frac {\partial L}{\partial {\vec {r}}}}=0\,.}$

Since the Euler-Lagrange equations are invariant under a coordinate transformation, it is irrelevant whether it is derived from the values ​​in the moving reference system or from the values ​​in the inertial system. So it follows in the moving frame of reference for the two terms ${\displaystyle K'}$ ${\displaystyle K}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\vec {v}}'}}={\frac {\mathrm {d} }{\mathrm {d} t}}m({\vec {v}}'+{\vec {\omega }}\times {\vec {r}}')=m{\vec {a}}'+m{\dot {\vec {\omega }}}\times {\vec {r}}'+m{\vec {\omega }}\times {\vec {v}}'}$

and

${\displaystyle {\frac {\partial L}{\partial {\vec {r}}'}}=m{\vec {v}}'\times {\vec {\omega }}+m({\vec {\omega }}\times {\vec {r}}')\times {\vec {\omega }}\,.}$

Inserted into the Euler-Lagrange equation, and converted to is ${\displaystyle m{\vec {a}}'}$

${\displaystyle m{\vec {a}}'=-m{\dot {\vec {\omega }}}\times {\vec {r}}'-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')-2m{\vec {\omega }}\times {\vec {v}}'}$

the listing of all forces in the rotating reference system, which occur in addition to the forces already caused by the potential in the inertial system.

What is the first term, the Euler force, the second centrifugal force and the last term the Coriolis force in the kinematic derivation . The equation shows that the Euler force and the centrifugal force in the rotating system only depend on the position of the body, which is indicated by the position vector , and also act on a body at rest. The Coriolis force, on the other hand, only acts on moving bodies (speed vector ) and is independent of the location; the deflection takes place in the same way at every location of the rotating system. ${\displaystyle {\vec {F}}_{\mathrm {C} }=-2m{\vec {\omega }}\times {\vec {v}}'}$ ${\displaystyle {\vec {r}}'}$ ${\displaystyle {\vec {v}}'}$

In the physical interpretation, the Euler force is the one that tries to keep a freely moving but resting body in place , whereas the centrifugal force tries to remove it from its place . The Coriolis force tried a moving body to a certain place due .

Since the Coriolis force does not meet the conditions for actio and reactio and only has to be accepted in the rotating reference system, it is called an inertial force . Formally, Newton's equation of motion also applies in the rotating reference system if apparent forces are taken into account. In contrast to the centrifugal force, the Coriolis force has the effect that the moving body tends to be brought back to the starting point of the movement . ${\displaystyle m{\vec {a}}={\vec {F}}}$

Since the Coriolis force is always perpendicular to the direction of movement of the body, it does no work on the body .

Special cases

The following special cases assume a constant angular velocity ( ). In the previously derived equation of motion, the external force, the centrifugal force and the Coriolis force must also be taken into account. ${\displaystyle {\dot {\vec {\omega }}}={\vec {0}}}$

${\displaystyle m{\vec {a}}'={\vec {F}}-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')-2m{\vec {\omega }}\times {\vec {v}}'}$

Movement can be explained by Coriolis acceleration

Is the movement z. B. limited by constraints to the surface of a body and if the external force and the centrifugal force compensate each other , we get: ${\displaystyle {\vec {F}}}$ ${\displaystyle -m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')}$

${\displaystyle {\vec {a}}'=-2{\vec {\omega }}\times {\vec {v}}'}$

Without restricting the general validity, only the component of the relative speed in a plane perpendicular to the axis of rotation is considered. The relative movement in this plane can only be explained with the Coriolis acceleration. Since the acceleration is always directed perpendicular to the velocity vector, there is a uniform circular motion with the radius : ${\displaystyle r^{*}}$

${\displaystyle a'={\frac {v'^{2}}{r^{*}}}=2\omega v'}$

The circle is traversed at twice the angular speed against the direction of rotation of the reference system. The radius results from:

${\displaystyle r^{*}={\frac {v'}{2\omega }}}$

These conditions can be achieved in the experiment with a rotating paraboloid (see visualization of the Coriolis effect ), but also occur approximately on earth with ocean currents.

Paraboloid

See also : Centrifugal force # Rotating liquid

Schematic: Harmonic oscillation on a parabolic shell. The curvature is exaggerated.

The frictionless movement of a body radially from the edge of a paraboloid with the cross section:

${\displaystyle y={\frac {h}{R^{2}}}\;r^{2}}$

is released, can be approximated with the differential equation:

${\displaystyle {\ddot {r}}+{\frac {2gh}{R^{2}}}\,r=0\rightarrow {\ddot {r}}+\Omega ^{2}\,r=0}$

to be discribed. It is the ordinate of the generating parabola at the radius and the acceleration due to gravity . When deriving the differential equation, it is taken into account that only the downhill force acts parallel to the surface . ${\displaystyle h}$ ${\displaystyle r=R}$ ${\displaystyle g}$

The solution to this differential equation is a harmonic oscillation with the angular frequency . ${\displaystyle \Omega }$

${\displaystyle r=R\cos(\Omega t)}$.

If the bowl rotates at the angular velocity appropriate to the shape , the period of the oscillation is exactly the same as the duration for one revolution of the bowl. ${\displaystyle \omega _{P}}$

${\displaystyle \omega _{P}^{2}={\frac {2gh}{R^{2}}}}$

The oscillation in the inertial system results in the circles explained above in the rotating system, the relative speed remaining constant for reasons of energy conservation. In the example assumed, the oscillation is a straight-line movement when viewed from above. In the rotating system, however, the movement is perceived as a circle with half the radius of the shell. ${\displaystyle v'}$

The movement in the rotating system is obtained through coordinate transformation in Cartesian coordinates :

${\displaystyle x'=r\cos(\alpha )}$.

${\displaystyle y'=-r\sin(\alpha )}$.

The angle denotes the angle by which the rotating system is rotated around the axis of rotation relative to the inertial system. With the solution of the oscillation equation of the assumed example we get with : ${\displaystyle \alpha =\omega _{P}t}$ ${\displaystyle r}$ ${\displaystyle \omega =\omega _{P}}$

${\displaystyle x'=R\cos(\omega t)\cdot \cos(\omega t)}$.

${\displaystyle y'=-R\cos(\omega t)\cdot \sin(\omega t)}$.

With the product formulas of trigonometry, we finally get a circle in parametric representation:

${\displaystyle x'={\frac {R}{2}}\left(1+\cos(2\omega t)\right)}$

${\displaystyle y'=-{\frac {R}{2}}\sin(2\omega t)}$.

If the body is given a tangential speed with or against the direction of rotation of the shell at the beginning, ellipses result from the outside. Since the size of the circles observed in the rotating system depends on the relative speed, small circles are achieved if the direction of rotation of the ellipse corresponds to that of the shell.

Disc experiment

The experiment demonstrates the influence of the Coriolis acceleration in a rotating reference system. The ideal case is dealt with in which no forces act between the body, which moves radially outward from the center point, and the disk, such as e.g. B. when a ball is thrown. The body therefore moves uniformly in a straight line when viewed from the outside, only the movement in the plane of the disk being considered. The relative velocity with respect to the disk is then the difference between the assumed constant speed of the body in the inertial frame and the rotational speed of the wheel: . The two terms are also the components of the relative velocity in the radial ( ) and tangential ( ) direction: , . ${\displaystyle {\vec {v}}'={\vec {v}}-{\vec {\omega }}\times {\vec {r}}'}$ ${\displaystyle {\vec {v}}'_{r}}$ ${\displaystyle {\vec {v}}'_{t}}$ ${\displaystyle {\vec {v}}'_{r}={\vec {v}}}$ ${\displaystyle {\vec {v}}'_{t}=-{\vec {\omega }}\times {\vec {r}}'}$

The inward Coriolis force due to the tangential speed is twice as great as the outward centrifugal force. ${\displaystyle {\vec {F}}_{\mathrm {C,r} }}$ ${\displaystyle v'_{t}}$

${\displaystyle {\vec {F}}_{\mathrm {C,r} }=-2m\,{\vec {\omega }}\times {\vec {v}}'_{t}=2m\,{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')}$

Both radially directed apparent forces add up to the force : ${\displaystyle {\vec {F}}_{r}}$

${\displaystyle {\vec {F}}_{\mathrm {r} }=m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')}$

It is just as great as the force that would be required if the body were firmly connected to the disk.

The equation of motion in the rotating reference system is simplified to:

${\displaystyle m{\vec {a}}'={\vec {F}}_{\mathrm {r} }-2m{\vec {\omega }}\times {\vec {v}}'_{r}\,.}$

The first term leads to a uniform circular motion. The second term is the Coriolis force due to the radial speed and contains the acceleration that is required to increase the peripheral speed. The superposition of the circular motion with a constant increase in the radius results in an Archimedean spiral .

Since the vector of the angular velocity is perpendicular to the disk, the amounts of the vectors can be used for calculations. The lateral deviation at the point with the radius is calculated with the Coriolis acceleration as: ${\displaystyle d}$ ${\displaystyle r}$ ${\displaystyle 2\omega \cdot v'_{r}}$

${\displaystyle d=\omega \cdot v'_{r}\cdot t^{2}=\omega \,t\cdot v'_{r}\cdot t=\alpha \cdot r}$.

Since the body on the disk is at a distance from the center point and the disk has rotated through the angle , the lateral deviation is thus equal to the corresponding arc length . If a disc connected to the point to be reached, it must therefore at the same angle maintained are. ${\displaystyle t}$ ${\displaystyle r}$ ${\displaystyle \alpha }$

Regardless of time, the geometric path is given in polar coordinates:

${\displaystyle \alpha ={\frac {\omega }{v'_{r}}}\cdot r}$ .

Devil's wheel

With a uniform movement in the rotating reference system, the relative acceleration is zero.

${\displaystyle {\vec {F}}-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}')-2m{\vec {\omega }}\times {\vec {v}}'={\vec {0}}}$.

This equation describes the “dynamic equilibrium” between the external force and the two inertial forces centrifugal force and Coriolis force. When trying to move radially towards the center of the disk, the centrifugal force and Coriolis force are perpendicular to each other and could therefore be distinguished. In addition to the fun factor, experiences with inertia are also conveyed.

Visualization of the Coriolis effect on earth

Object that moves smoothly over the surface of a paraboloid. Top view of the paraboloid.

left: elliptical movement viewed from the outside.

right: Circular movement against the direction of rotation of the bowl in the rotating system.

An experiment that demonstrates the Coriolis force as the sole reason for an effect is not easy to carry out. While air and frictional resistance can largely be suppressed, a moving body on a flat turntable is always subject to the combined effect of centrifugal and Coriolis forces.

The isolated effect of the Coriolis force can be demonstrated on a bowl that is filled with a liquid that hardens in air while the bowl rotates at a constant angular velocity; In this way, a paraboloid of revolution is physically established which has an equipotential surface .

On the stationary paraboloid shell, a body that is placed on any non-central point will, due to the downhill force, execute a harmonic oscillation that goes through the lowest point of the disk. However, if the shell rotates at the angular velocity that was used for the paraboloid coating, it will remain in place, since the resultant of weight and centrifugal force is perpendicular to the surface. If the body moves on the rotating bowl, it ideally describes a circle ("inertial circle"), the direction of rotation of which is opposite to the rotation of the bowl, and which is caused exclusively by the Coriolis force.

The experiment on the paraboloid can serve as a model for inertial movements on Earth. In contrast to the shell, the earth's body is convexly curved, but has assumed the shape of an ellipsoid of revolution due to displacement of mass in the course of the earth's history. The force of gravity on its surface results from the interaction of gravitation and centrifugal force: the resultant is perpendicular to the surface.

Coriolis force due to the earth's rotation

Movement on the earth's surface and Coriolis parameters

Division of the earth's angular velocity into horizontal and vertical components based on geographical latitude ${\displaystyle \varphi }$

The Coriolis parameter on earth as a function of latitude

Any object moving on the earth will be deflected by the Coriolis acceleration because the earth is a rotating system. The only exceptions are movements parallel to the earth's axis , e.g. B. at the poles the vertical movements up or down, at the equator the horizontal movements due north or south. The influence of the Coriolis acceleration on the direction of movement can most easily be visualized using a spherical earth figure; For the study of motion sequences under the influence of the forces involved , a more precise model of the earth's shape must be used (cf. visualization of the Coriolis effect on earth ).

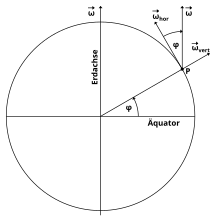
For the consideration of movements in any geographical latitude , it makes sense to split the vector of the angular velocity of the earth into a horizontal component in south-north direction and a vertical component . The following then applies: ${\displaystyle \varphi }$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {\omega }}_{\text{hor}}}$ ${\displaystyle \ {\vec {\omega }}_{\text{vert}}}$

${\displaystyle {\vec {\omega }}_{\text{hor}}={\vec {\omega }}\cos \varphi }$

${\displaystyle {\vec {\omega }}_{\text{vert}}={\vec {\omega }}\sin \varphi }$

To calculate the Coriolis force in the case of horizontal movements, it is advantageous to combine the constant values for a location in a certain geographical latitude into a Coriolis parameter : ${\displaystyle \varphi }$

${\displaystyle \textstyle f_{\mathrm {C} }=2\,\omega \,\sin \varphi }$

The earth's rotation (one revolution in 23 hours 56 minutes 4 seconds = 1  sidereal day = 86164 s) takes place at a constant angular velocity of

${\displaystyle \omega ={\frac {2\pi }{86164\,\mathrm {s} }}=7{,}2921\cdot 10^{-5}\,{\mathrm {rad\,s} }^{-1}}$.

In mid-northern latitudes, the Coriolis parameter is thus in the typical order of magnitude of . ${\displaystyle \textstyle f_{\mathrm {C} }\approx \,10^{-4}\,{\mathrm {rad\,s} }^{-1}}$

Bodies that move horizontally with speed - i.e. parallel to the surface of the earth - are deflected laterally by the Coriolis acceleration and the Coriolis acceleration perpendicular to the earth's surface: ${\displaystyle {\vec {v}}_{\text{hor}}}$ ${\displaystyle {\vec {a}}_{\text{hor}}}$ ${\displaystyle {\vec {a}}_{\text{vert}}}$

${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{vert}}\times {\vec {v}}_{\text{hor}})}$

${\displaystyle {\vec {a}}_{\text{vert}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{hor}})}$

The horizontal acceleration plays a more important role in the higher geographical latitudes, while near the equator mainly only the vertical acceleration is effective for movements in an east-west direction. ${\displaystyle {\vec {a}}_{\text{hor}}}$ ${\displaystyle {\vec {a}}_{\text{vert}}}$

Horizontal movements

Coriolis force when moving relative to the earth's surface:
A speed to the east leads to an acceleration to the south in the northern hemisphere, a speed straight up to a deflection to the west ${\displaystyle v_{\text{Norm}}}$

With the Coriolis parameter , the Coriolis acceleration for movements with the speed has the amount: ${\displaystyle \textstyle f_{\mathrm {C} }=2\,\omega \,\sin \varphi }$ ${\displaystyle {\vec {a}}_{\text{hor}}}$ ${\displaystyle {\vec {v}}_{\text{hor}}}$

${\displaystyle \left\vert {\vec {a}}_{\text{hor}}\right\vert =f_{\mathrm {C} }\,\left\vert {\vec {v}}_{\text{hor}}\right\vert }$

This acceleration leads to a change in direction of movement to the right in the northern hemisphere and to the left in the southern hemisphere. It disappears at the equator and is maximal at the poles.

If the speed is divided into components in the east or north direction, the corresponding components of the Coriolis acceleration result from executing the cross product in the coordinate directions x = O, y = N: ${\displaystyle {\vec {v}}_{\text{hor}}}$

${\displaystyle {\vec {a}}_{\text{hor}}={\begin{pmatrix}a_{\text{O}}\\a_{\text{N}}\\0\end{pmatrix}}=f_{\mathrm {C} }{\begin{pmatrix}v_{\text{N}}\\-v_{\text{O}}\\0\end{pmatrix}}}$

The accelerations resulting from a Coriolis parameter of are very low. Even with a gun, the projectile has a horizontal speed of 1000 m / s, we have: . At a distance of 40 km, the assumed values ​​result in a deviation of only 80 m. Significantly greater effects occur with meteorological phenomena in which an extremely low acceleration lasts for a very long time. ${\displaystyle \textstyle f_{\mathrm {C} }=10^{-4}\,{\mathrm {rad\,s} }^{-1}}$ ${\displaystyle a_{\text{hor}}=0{,}1\,{\mathrm {m\,s} }^{-2}}$

When moving in the direction of rotation of the earth, i. H. to the east, the influence of the vertical component of the Coriolis acceleration theoretically causes a slight increase outside the narrower polar regions, while movements in the other direction cause a slight decrease; this effect is called the Eötvös effect . ${\displaystyle {\vec {a}}_{\text{vert}}}$

${\displaystyle a_{\text{vert}}=2\,\omega \,\cos \varphi \cdot v_{\text{O}}}$

North-south directed movements are not affected vertically. However, this effect is mostly negligible, since the gravitational acceleration in the same direction is much more noticeable. In practice, the vertical component of the Coriolis force only plays a role as a correction element in precision measurements of the earth's gravity field . It disappears at the poles and is maximally at the equator. She makes z. For example, an airplane that flies there at a speed of approx. 1000 km / h to the east is almost a thousandth of its weight lighter - if it flies to the west, it becomes correspondingly heavier. Therefore, when describing the purely horizontal ocean or air currents, the “Coriolis force” is often only used to describe its horizontal component. For them, as for the example of the horizontal turntable explained above, the Coriolis force always acts perpendicular to the direction of movement and that its strength does not depend on the direction of movement.

Coriolis force and Foucault's pendulum

→ Main article : Foucault's pendulum

In the northern hemisphere, the Coriolis force causes the plane of oscillation of the Foucault pendulum to rotate clockwise, as the pendulum is constantly being deflected to the right. The slight deviations of the individual oscillations add up to a daily total deviation of for a Foucault pendulum in geographical latitude , so that the deviation of the individual oscillation already represents experimental evidence for the rotation of the earth. At the pole, the oscillation plane rotates once a day by 360 degrees and decreases with the sine of the geographical latitude towards the equator to zero. In the southern hemisphere, the sign of the sine changes and the pendulum rotates counterclockwise. In general, the following applies to the time of a complete rotation of the plane of oscillation: ${\displaystyle \alpha =360^{\circ }\sin \varphi }$ ${\displaystyle \varphi }$

${\displaystyle T={\frac {2\pi }{\omega \,\left|\sin \varphi \right|}}}$.

Influence of the Coriolis force on currents

Influence of the Coriolis force on the water currents

Beta effect: The change in the Coriolis force with geographic latitude causes a slightly spiral expansion of the inertial circle

Large-scale oceanic currents arise with the participation of the Coriolis force

The Coriolis force has a significant influence on the directions of large-scale movements in the oceans, both directly and through the influence of the wind, which is also controlled by the Coriolis force. Since the Coriolis force is independent of the cardinal direction of a horizontal movement, a mass of air or water that moves in the frame of reference of the earth with the speed without the influence of other forces describes "circles of inertia" with radii of: ${\displaystyle v_{\text{hor}}}$

${\displaystyle R={\frac {v_{\text{hor}}}{f_{C}}}={\frac {v_{\text{hor}}}{2\omega \,\sin \varphi }}}$

In middle latitudes with values ​​of the Coriolis parameter of and a typical ocean current speed of, the result is a radius of The movement takes place clockwise in the northern hemisphere and counterclockwise in the southern hemisphere. The period of the orbital movement is: ${\displaystyle f_{C}=10^{-4}\,\mathrm {rad\,s} ^{-1}}$ ${\displaystyle 10^{-1}{\tfrac {\mathrm {m} }{\mathrm {s} }}}$ ${\displaystyle R=1\,\mathrm {km} .}$

${\displaystyle T={\frac {2\pi }{f_{C}}}={\frac {2\pi }{2\omega \,\sin \varphi }}={\frac {43082\,\mathrm {s} }{\sin \varphi }}}$

At 60 degrees latitude, the period is around 14 hours. At the poles, the minimum is 11 hours 58 minutes 2 seconds (half the length of the sidereal day), while the period towards the equator approaches infinity, so that no circles of inertia occur in the inner tropics. The Coriolis force also determines the direction of rotation of the tidal wave in the deep ocean, which leads to different high and low tide times along a coast. ${\displaystyle T}$

Because of the latitude dependence of the Coriolis parameter, the “circles of inertia” are not circles in the mathematical sense, but only as a first approximation, as they have a smaller radius on the pole side than on the equator side. This results in a slight spiral shape, as a result of which the moving mass is not returned exactly to the starting point, but is shifted slightly to the west; this modification of the inertia circles is called the “beta effect”. The movement on circles of inertia could be verified by observing the flow displacement of floating buoys in the Baltic Sea. If the inertial movement is superimposed as a rotation by a large-scale ocean current as a translation, a cycloidal movement pattern results .

A turbulent boundary layer occurs at the interface between the atmosphere and the ocean, both in the air and in the water . In the ocean, the turbulent boundary layer ensures that the medium is mixed in its entire extent. At the boundary layer, a wind with a predominant direction exerts a certain shear stress through friction , which sets a water flow in motion in the same direction ( Ekman transport ). However, this is deflected by the Coriolis force to the right on the northern hemisphere and to the left on the southern hemisphere. One consequence of this diversion is what is known as “ Ekman pumping ”, which can be observed in the central and eastern Pacific , for example . The surface water, which in the area of ​​constant trade winds is driven westwards from the east, is diverted to the right near the equator on the northern hemisphere and to the left on the southern hemisphere; this divergence is compensated for by swelling, cooler deep water, so that an equator-parallel strip of cooler water temperature appears.

Inertial circles impede the horizontal movement of water caused by the object's ascent when the system is in rotation.

The surface water flow generated in this way is also slowed down by the layer of water underneath, reducing both the speed and the Coriolis force that depends on it. This braking effect continues down to a certain depth (Ekman depth) until the flow is completely slowed down. Up to this point, the Coriolis force also acts - increasingly weakened - so that a spiral-like structure is formed overall ( corkscrew flow ). Large- scale movements in the ocean ( Sverdrup relation ) are also significantly influenced by the Coriolis force.

In general, the influence of the Coriolis force on certain movements in the sea and in the atmosphere is characterized by the dimensionless Rossby number . The smaller this is, the stronger the movement is influenced by the Coriolis force.

Contrary to popular belief, the direction of rotation of small-scale water currents such as the vortex of a draining bathtub is not determined by the Coriolis force.

The effect of the Coriolis force is also demonstrated by experiments on a small scale that Geoffrey Ingram Taylor first published in 1921. The distribution of a small amount of one liquid in another, with which it is completely miscible , but from which it differs by certain parameters, can be suppressed when the other liquid is in a rotational movement. In this way, added ink forms a column-like structure (“Taylor column”) in a rotating water container, which remains for a long time. The reason is that the diffusing particles rotate in inertial circles in the opposite direction to the container rotation.

A tennis ball, which is released in a rotating water tank, rises at a slower speed than in a non-rotating one, since the movement of the water flowing horizontally below or displaced above is hindered by the formation of inertial circles. Through these experiments it becomes clear that the tendency of the Coriolis force is to bring the moving particles back to the starting point.

Influence of the Coriolis force on the atmospheric circulation

Geostrophic wind due to the interaction of gradient force and Coriolis force ${\displaystyle F_{G}}$ ${\displaystyle F_{C}}$

Ageostrophic wind through the interaction of gradient force, Coriolis force and friction force ${\displaystyle F_{G}}$ ${\displaystyle F_{C}}$ ${\displaystyle F_{R}}$

Air currents in the earth's atmosphere are generally not inertial movements, but are caused both on a small and large scale by pressure differences that are the result of locally or regionally different irradiation . A gradient force acts between the areas with high and low air pressure , which can bring about the pressure equalization.

In large-scale air currents over several hundreds or thousands of kilometers, the Coriolis force plays an important role despite its small size, as it deflects the air masses and prevents the direct air movement from high to low . In the free atmosphere the Coriolis force can completely compensate for the horizontal component of the gradient force , the wind is thereby deflected to an isobaric-parallel flow, the geostrophic wind , in which the gradient force directed towards the low and the Coriolis force directed towards the high balance each other. This prevents pressure equalization and the pressure areas remain stable for a few days or weeks. The jet streams at a height of a few kilometers are an impressive example of geostrophic winds .

In the atmospheric base layer close to the ground, however, a considerable frictional force acts on the air flow; its vector is opposite to the flow vector. This friction, the effect of which is propagated vertically up to a certain height, slows the flow and thus reduces the magnitude of the Coriolis force. For the flow, on the one hand the downward gradient force and on the other hand the upward force component, which results from the vectorial addition of the frictional force and the Coriolis force, are decisive. As a result, the ageostrophic flow (frictional wind ) no longer runs parallel to the isobars, but transversely to the isobars from the high to the low pressure area, as can be seen on ground weather maps .

With increasing altitude, the effect of the ground friction decreases and the influence of the Coriolis force becomes stronger: the wind increases and the wind direction turns - in the northern hemisphere - to the right, until the wind has taken on a geostrophic character at a higher altitude. This creates a wind shear between the ground and the height ; By connecting the tips of the wind vectors at increasing heights, a spiral curve ( Ekman spiral ) is obtained.

The interaction of these forces also explains the course of the trade winds that blow from the subtropical high pressure belt to the equatorial low pressure area. The Coriolis force deflects this flow on both hemispheres to a westward eastward flow (“Urpassat”); Due to the influence of friction, this becomes the north-east trade wind in the near-ground layer of the northern hemisphere and the south-east trade wind in the southern hemisphere . The north-east trade wind is therefore a (geostrophic) east-west current that is deflected near the ground towards the equator and not - as is often shown on sketches - a north-south current that is deflected to the west.

Effect of the Coriolis force on a large-scale wind system, here low pressure area near Iceland (northern hemisphere)

Formation areas and trajectories of tropical cyclones

In the northern hemisphere, the air flows clockwise in high pressure areas and counterclockwise in low pressure areas. In the southern hemisphere, the direction of rotation is reversed. Near the ground, the air leaves the high pressure area in the form of a right-turning vortex, i.e. clockwise, and flows counter-clockwise into the low pressure area, where this vortex movement is generally visible through cloud formation. Since the vector of the angular velocity is parallel to the earth's surface at the equator, the horizontal component of the Coriolis force is not effective there, dynamic high and low pressure areas cannot exist near the equator. This applies in particular to tropical cyclones , which - although the thermal conditions exist at the equator - only arise at a distance of at least around five degrees of latitude to the north or south.

Due to radiation, there is a temperature and pressure gradient on earth from the tropics to the polar regions, with the horizontal gradient being particularly pronounced in the upper troposphere . The pressure decrease is not even towards the pole, but is concentrated at the upper edge of the troposphere on a relatively narrow band with a strong drop in air pressure, which is visible on altitude weather maps through a dense cluster of isobars. In this area there is a strong geostrophic current, which increases regionally to the jet streams. This zone of the strong air pressure gradient does not run parallel to the latitude, but rather as a more or less meandering structure ( Rossby waves ) with wavelengths and amplitudes of up to a few thousand kilometers. The waves move slowly from west to east, analogous to the direction of the geostrophic flow, but can also remain stationary for a longer period of time. Mass shifts in the area of ​​the Rossby waves create low pressure areas (cyclones) on the pole side and high pressure areas (anticyclones) on the equatorial side, which usually reach down to the surface of the earth. In these dynamic, circular pressure structures, there is a balance of gradient, centrifugal and Coriolis force. While the first two forces can be viewed as constant for a pressure area, the Coriolis force in these spatially extended (≥ 1000 km) pressure areas is greater on the polar side than on the equator side. As a result, the cyclones tend to shear in a polar direction on average, the anticyclones in the equatorial direction. As a result, the subpolar low pressure zone forms north of the polar frontal zone and the subtropical high pressure belt south of it . In this respect, the Coriolis force determines not only the course of the atmospheric air currents, but also the distribution of the large-scale pressure areas on earth.

The geostrophic equilibrium only shapes the large-scale weather patterns. The Coriolis force has no significant influence on the direction of rotation of small-scale low pressure areas, for example tornadoes , since the other effective forces far outweigh the Coriolis force in terms of magnitude. The fact is already clear that in tornadoes in the northern hemisphere and rotations with possible direction.

Vertical movements

→ Main article : Trap experiments to prove the rotation of the earth

If a body falls from a height in free fall , it does not hit the exact point that is located below it in the perpendicular direction from the starting point, but rather it is deflected by the Coriolis acceleration during the fall time. Since the vectors are perpendicular to each other, the cross product in a Cartesian coordinate system with x = east results in an east deflection: ${\displaystyle h}$

${\displaystyle {\vec {a}}_{\text{hor}}=-2\,{\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{vert}}={\begin{pmatrix}a_{\text{Ost}}\\a_{\text{Nord}}\\0\end{pmatrix}}=-2\omega \cos \varphi \,{\begin{pmatrix}v\\0\\0\end{pmatrix}}}$

The deviation is maximum at the equator ( ) and is zero at the poles ( ). By substituting for free fall, you get a deviation to the east by integrating twice according to the time : ${\displaystyle \varphi =0^{\circ }}$ ${\displaystyle \varphi =\pm 90^{\circ }}$ ${\displaystyle v=-g\,t}$ ${\displaystyle d_{\text{Ost}}}$ ${\displaystyle t}$

${\displaystyle a_{\text{Ost}}=2\,\omega v\cos \varphi =2\,\omega g\,t\cos \varphi }$

${\displaystyle v_{\text{Ost}}=2\,\omega g\cos \varphi \int t{\text{d}}t=\omega g\,\cos \varphi \,t^{2}}$

${\displaystyle d_{\text{Ost}}=\omega g\,\cos \varphi \int t^{2}{\text{d}}t={\frac {1}{3}}\omega g\,\cos \varphi \,t^{3}}$

With the fall time we get: ${\displaystyle t={\sqrt {\frac {2h}{g}}}}$

${\displaystyle d_{\text{Ost}}={\frac {1}{3}}\omega g\,\cos \varphi \,t^{2}{\sqrt {\frac {2h}{g}}}={\frac {2}{3}}\omega \,\cos \varphi \,h{\sqrt {\frac {2h}{g}}}}$

The east deviation in turn leads to a very small south deviation in the northern hemisphere, but this becomes zero both at the equator and at the pole. A north deviation would accordingly be expected in the southern hemisphere:

${\displaystyle d_{\text{Süd}}={\frac {2}{3}}\omega ^{2}\cos \varphi \cdot \sin \varphi \cdot {\frac {h^{2}}{g}}={\frac {1}{3}}\omega ^{2}\sin 2\varphi \cdot {\frac {h^{2}}{g}}}$

Mersenne's thought experiment

Historical caricature on the Mersenne experiment

An old question about which as early as the 17th century. Marin Mersenne speculated, is the one where a cannonball shot vertically upwards hits the ground again - regardless of air movement and air resistance.

The vertical speed of the cannonball follows the speed-time law during flight : ${\displaystyle v}$

${\displaystyle v=v_{0}-g\,t}$

Inserted into the east component of the Coriolis acceleration, the integration of the acceleration results in a westerly speed component (negative east component) that reaches its maximum at the turning point and decreases again during the descent. At the bottom it reaches zero again.

${\displaystyle v_{\text{West}}=2\omega \,\cos \varphi \left(v_{0}\,t-\,{\frac {1}{2}}gt^{2}\right)}$,

or by reintegrating the distraction:

${\displaystyle d_{\text{West}}=2\omega \,\cos \varphi \left({\frac {1}{2}}v_{0}t^{2}-\,{\frac {1}{6}}gt^{3}\right)}$

After the time the ball has reached the ground again. The total offset to the west results in: ${\displaystyle t=2{\frac {v_{0}}{g}}}$

${\displaystyle d_{\text{West}}={\frac {4}{3}}\omega {\frac {v_{0}^{3}}{g^{2}}}\cos \varphi }$.

Ascent and descent each contribute half of the total deviation. At 50 ° latitude and an initial speed of 100 m / s ( ascent height approx. 500 m), the westerly deviation is theoretically 65 cm. The offset is greatest at the equator; there is no difference between the northern and southern hemispheres. ${\displaystyle v_{0}^{2}/{2g}}$

The following example serves as a plausibility check, which is based on the simplified notion that the horizontal speed is maintained. Since the earth continues to rotate during the vertical movement, this is only approximately the case. If the calculation is correct, the deviation is lower by a factor of 2/3.

Near the equator, next to a tower, a cannon fires a bullet vertically upwards so that it reaches the top of the tower. The tower and cannon are firmly connected to the earth and, viewed from the extraterrestrial inertial system (IS), rotate at angular velocity ; however, the orbital speed at the top of the tower is greater than at the earth's surface. In addition to its vertical speed, the fired ball initially has the orbital speed of the earth's surface and would like to maintain this on its way. ${\displaystyle h}$ ${\displaystyle \omega }$ ${\displaystyle \omega \cdot h}$

Since the ball has a lower horizontal speed during the entire flight, i.e. a lower east component than a point on the tower at the same height, it deviates more and more to the west compared to the vertical up to the distance at the turning point. ${\displaystyle d_{W}}$

Even during the subsequent free fall, the ball continues to maintain its horizontal speed, so that the ball remains increasingly further west compared to the tower. Once at the base point, the horizontal velocities of all bodies agree again. Since the free fall lasts as long as the ascent, the total deviation is . A ball that is released at the top of the tower during the reversal time for comparison starts with the horizontal speed of the top of the tower and maintains this up to the base point, so that it deviates to the east compared to the base point (see "Vertical movements"). Off the equator must be replaced by. ${\displaystyle d_{\text{West}}=2d_{W}}$ ${\displaystyle \omega }$ ${\displaystyle \omega \cos \varphi }$

Synoptic overview of the deflection directions on earth

The expressions for the components of the Coriolis acceleration apply equally to the entire earth body. The directions are seen from the position of the observer in his respective geographical latitude . The middle column describes the Eötvös effect. ${\displaystyle \varphi }$

In the southern hemisphere, the vertical vector is exactly the opposite of the corresponding vector in the northern hemisphere . This results in a deviation to the left for the observer in the southern hemisphere with horizontal movements. ${\displaystyle {\vec {\omega }}_{\text{vertS}}}$ ${\displaystyle {\vec {\omega }}_{\text{vertN}}}$

When thrown vertically upwards, there is a deflection to the west. When throwing with a subsequent free fall, however, both directions of deflection must not be added one after the other; this case is dealt with in the chapter “The Mersenne Thought Experiment”.

Distraction due to the Coriolis acceleration on earth depending on the geographical latitude

Geographical latitude φ	horizontal movement (in any direction)		horizontal movement (east / west)		vertical movement (free fall)
	horizontal distraction		vertical deflection		horizontal distraction
	equation	direction	equation	direction	equation	direction
North Pole (90 ° N)	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{vert}}\times {\vec {v}}_{\text{hor}})}$	right	-	-	-	-
Northern Hemisphere (0 ° <φ <90 ° N)	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{vert}}\times {\vec {v}}_{\text{hor}})}$	right	${\displaystyle {\vec {a}}_{\text{vert}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{hor}})}$	up down	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{vert}})}$	east
Equator (0 °)	-	-	${\displaystyle {\vec {a}}_{\text{vert}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{hor}})}$	up down	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{vert}})}$	east
Southern Hemisphere (0 ° <φ <90 ° S)	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{vertS}}\times {\vec {v}}_{\text{hor}})}$	Left	${\displaystyle {\vec {a}}_{\text{vert}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{hor}})}$	up down	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{hor}}\times {\vec {v}}_{\text{vert}})}$	east
South Pole (90 ° S)	${\displaystyle {\vec {a}}_{\text{hor}}=-2\,({\vec {\omega }}_{\text{vertS}}\times {\vec {v}}_{\text{hor}})}$	Left	-	-	-	-

Coordinate systems

The Coriolis acceleration is experienced by a body that moves in a rotating reference system. For this, the formula is generally: . In some typical coordinate representations for rotating systems, the formulas are as follows: ${\displaystyle {\vec {a}}_{\mathrm {C} }}$ ${\displaystyle {\vec {a}}_{\mathrm {C} }=-2\,{\vec {\omega }}\times {\vec {v}}'}$

Cylindrical coordinates	Spherical coordinates	geographic coordinates
${\displaystyle {\begin{pmatrix}a_{\mathrm {C} ,r}\\a_{\mathrm {C} ,t}\\a_{\mathrm {C} ,z}\end{pmatrix}}=-2\,\omega {\begin{pmatrix}-\,v_{t}\\v_{r}\\0\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}a_{\mathrm {C} ,r}\\a_{\mathrm {C} ,\theta }\\a_{\mathrm {C} ,\varphi }\end{pmatrix}}=-2\,\omega {\begin{pmatrix}-\,v_{\varphi }\sin \theta \\-v_{\varphi }\cos \theta \\v_{r}\sin \theta +v_{\theta }\cos \theta \end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}a_{\mathrm {C} ,h}\\a_{\mathrm {C} ,\varphi }\\a_{\mathrm {C} ,\lambda }\end{pmatrix}}=-2\,\omega {\begin{pmatrix}-\,v_{\lambda }\cos \varphi \\-v_{\lambda }\sin \varphi \\v_{h}\cos \varphi -v_{\varphi }\sin \varphi \end{pmatrix}}}$

It is

• ${\displaystyle \omega }$the angular velocity of the reference system and
• ${\displaystyle {\vec {v}}'}$ is the velocity vector of the movement of the body, relative to the rotating reference system, and denotes
  • In the case of cylindrical coordinates, the index is the component parallel to the axis of rotation and the indices and the radial and tangential component perpendicular to the axis of rotation, ${\displaystyle z}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle r}$ ${\displaystyle t}$
  • For spherical coordinates, the index is the distance to the origin and the indices and the azimuth and polar angles, ${\displaystyle r}$ ${\displaystyle \varphi }$ ${\displaystyle \theta }$
  • For the geographic coordinates, the index is the distance to the surface of the sphere and the indices and the geographic latitude and longitude. ${\displaystyle h}$ ${\displaystyle \varphi }$ ${\displaystyle \lambda }$

If the movement takes place in a plane perpendicular to the axis of rotation, the angle between the velocity vector and the angular velocity vector is 90 °. Instead of calculating the cross product of the velocity and angular velocity vector, the magnitude of the Coriolis force can be used to determine the magnitude and the following applies:

${\displaystyle F_{\mathrm {C} }=2m\omega \,v'}$

Coriolis force in technology

Principle of a rotation rate sensor. With a rotated tuning fork, the prongs move laterally past each other in addition to normal movement. This movement is based on the Coriolis force.

Coriolis forces are important in technology when a rotary movement is "superimposed" by a second movement. This is the case, for example, with a robot that rotates and at the same time extends its gripper arm.

• If a load moves inwards or outwards on the boom of a crane while the crane is turning, it does not hang vertically downwards due to the Coriolis force, but is deflected to the side. If the load is retracted inwards along the boom, it leads the crane to rotate.

• In gear technology ( coupling gear ) and in robotics , the Coriolis forces play a role, since here too there are simultaneous movements along several degrees of freedom. If rotating reference systems are used to simplify the description, Coriolis forces occur for movements in these reference systems.

• The Coriolis mass flow meter is used to measure the mass flow of liquids or gases flowing through . The measuring tube is made to vibrate. These are measured and compared in the inlet and outlet. With the Coriolis balance , bulk goods in particular are measured by measuring the change in the required torque of a rotor plate.

• In centrifugal pumps , the medium is set in rotation by the pump wheel from the suction channel , which is usually located axially, and is thrown outward to the outlet by centrifugal force. The medium exerts Coriolis forces on the pump wheel, which results in a braking torque for the drive. The energy actually expended by the pump is roughly proportional to the radial mass flow, the radius of the pump wheel and the speed (disregarding turbulence, backflows and friction).

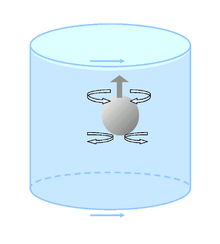
• Some yaw rate sensors for measuring angular velocities use the Coriolis force in the form of the so-called “tuning fork principle”, which is explained in the adjacent picture. Due to the rotary movement, the prongs of the tuning fork not only move towards each other, but they also perform lateral movements to each other, which are caused by the Coriolis force. The lateral deflection is approximately proportional to the angular velocity and can be detected, for example, by a capacitive or inductive measurement.

Didactic aspects

Academic instruction

In numerous textbooks and reference works, unclear and often incorrect statements about the Coriolis force have been found and still are to this day, especially with regard to its application to the physics of the earth, for example in meteorology and geosciences.

Simple but incorrect derivation of the Coriolis effect from the orbital speeds of the earth's surface in different latitudes

George Hadley's model of atmospheric circulation (1735) has been preserved in many textbooks as a standard didactic model due to its catchiness up to the most recent times. The main idea is that meridional air currents maintain their parallel to the latitude circle velocity component and thereby lag behind the earth's rotation when moving towards the equator, resulting in a westward directed current. This primarily includes an explanation of the north-east and south-east trade winds, but also the prevailing westerly winds north of the subtropical westerly wind belt. Because of this, at least in the statistical mean, correct description of the direction of flow, the Hadley model is sometimes viewed as a justified simplification, even if it only explains the deflection of meridional movements, but by no means parallel to latitude.

Behind the Hadley model stands the wrong physical concept of maintaining the velocity parallel to the latitude; in the quantitative result it leads to the Coriolis acceleration , so it is too small by half. It is also not taken into account that the Hadley model would result in wind speeds of a completely unrealistic order of magnitude even at relatively short distances of less latitude. The attempt to explain the non-occurrence of such speeds in reality with the additional hypothesis of a braking effect of friction only shifts the problem to another unrealistic effect: the required friction should have braked the rotation of the earth much more strongly in the course of its history. An air flow that would be caused solely by the different orbital speeds would lead to inertial circles that would reverse the direction of the air after a relatively short distance. A purely mechanical model that explains the atmospheric circulation only as an inertial movement does not do justice to the actual conditions. Flohn pointed out as early as 1960 that a circulation model based on Hadley's ideas is incompatible with the measured meteorological data. ${\displaystyle a_{c}=-\omega _{\text{vert}}\times v}$

Research history

Since the 16th century, the discussion of the Copernican view of the world has been speculating about the possible diversion from linear movements on earth. It was the anti-Copernicans who disputed the earth's own rotation, arguing, among other things, that a body would have to remain against the earth's rotation when it fell free on a rotating earth, that is, it would be deflected to the west; however, such a deflection could not be determined experimentally.

Accordingly, the discussion initially focused on deflecting vertical movements. Galileo correctly recognized that a deflection to the east should actually appear in the case of free fall, but this was also not experimentally verifiable at the time. Robert Hooke and Isaac Newton recognized in 1679 that free fall could not take place in a straight line, they assumed an elliptical orbit instead.

George Hadley considered large-scale horizontal movements on earth for the first time and in 1735 formulated a hypothesis for the formation of tropical trade winds based on the difference in the rotational speed of the earth in different geographical latitudes.

Leonhard Euler tried to derive the equations of motion mathematically, but the term for the deflection of a uniform motion was still incorrect.

The actual “discoverer” of the Coriolis effect is usually named Pierre Simon Laplace, who in 1775 derived the system of equations of motion for the surface of rotating planets and thus found a mathematically correct expression for the deflecting force for the first time; however, it did not go beyond the Hadley model in physical interpretation. Giovanni Battista Guglielmini (1791) in Bologna , Johann Friedrich Benzenberg (1802) in Hamburg's Michaeliskirche and in a mining shaft in the Ruhr area, and Ferdinand Reich (1832), also in a mine, provided pioneering work for experimental confirmation by measuring the deviation from the perpendicular direction in Freiberg in Saxony. In spite of the strong scatter , the results of Benzenberg's experiments agreed on average with the values calculated by Laplace and Gauss . An additional south deviation was found in various tests as early as the middle of the 19th century. In 1851, Léon Foucault was also able to experimentally confirm the horizontal deflection with the pendulum test named after him .

→ Main article : Fall experiments to prove the earth's rotation  and Foucault's pendulum

Gaspard Gustave de Coriolis (1792–1843)

In 1835 Gustave Coriolis mathematically analyzed the movement of machine parts that move relative to rotation. He found that the entire inertial force is made up of the centrifugal force and another, "composite" centrifugal force that causes a deflection. The latter was only referred to as the "Coriolis force" in the 20th century. Siméon Denis Poisson then calculated the deflection of artillery projectiles in 1838. In 1847 Joseph Bertrand presented a simplified kinematic derivation to the Paris Academy of Sciences , which later found its way into numerous textbooks. The deflection of the Foucault pendulum (1851) was considered the first reliable experimental confirmation. William Ferrel emphasized in 1858 that, contrary to the ideas of George Hadley, air currents in each direction in the northern hemisphere are deflected to the right (southern hemisphere to the left). Ferrel was the first to recognize movement on inertial circles and the dependence of their size on both the speed of movement and the latitude.

In 1879 Adolf Sprung founded the diversion of movements parallel to the latitude. He transferred the mathematical derivations applicable for a rotating flat disk to the system of a parabolic surface, in which the influence of the centrifugal force can be compensated so that the Coriolis effect can be viewed in isolation. Persson is of the opinion that Newton could have found this solution with his possibilities.

In the 1850s, the earth moved into the focus of research as a rotating system. The natural scientist Karl Ernst von Baer postulated a “general law” that the valleys of the great lowland currents in the northern hemisphere had a steeper right bank and a flatter left bank as a result of the Coriolis force. However, he limited the reasoning expressly to rivers in a meridional direction; Apparently existing river sections with steeper left bank he explained with the effectiveness of other factors. However, this theory was highly controversial among geoscientists and was very controversial, especially in the 1920s, in meteorological and geoscientific journals. On the one hand, the small size of the Coriolis force was mentioned, on the other hand, reference was made to the long periods of effectiveness. One cause of the controversy was the unclear conceptual separation between the Coriolis force and the "distracting force of the earth's rotation", which some authors have defined more broadly. A statistically valid proof of a greater frequency of steeply sloping valleys in the northern hemisphere was neither presented by Baer nor by other authors. The talasymmetry was only systematically researched geomorphologically from the middle of the 20th century and understood as multi-causal, with geological, tectonic and climatic factors acting together. In more recent works on geomorphology and geology, the "Baer law" no longer plays a role.

The problem of the meandering of rivers is closely linked to the flow behavior . Albert Einstein pointed to the role of the Coriolis force, in addition to centrifugal force, in the formation of river meanders (“ teacup effect ”) without discussing the quantitative relationship between the forces involved.

The idea that the movement of railroads is influenced by the Coriolis force and could lead to increased one-sided wear on tracks that are only used in one direction, comes from Braschman (1861) and has long been used in numerous textbooks in the sense of a given fact shown; there is no evidence of this in a technical publication. Helmut Vogel points out that the smallest irregularities in the track layout in the order of 0.1 mm have a far greater effect on the asymmetry of wear.

The experiences that Fridtjof Nansen had made on his Fram expedition in the Arctic led him to the assumption that the course of the drifting current is influenced by the earth's rotation. The thoughts developed by Ekman then led to the discovery of the Ekman spiral. The concept of internal waves also goes back to Nansen's observations.

The term "Coriolis force" has only been in use since the 1920s, before "distracting force" was a common term.

literature

• D. Meschede: Gerthsen Physik . 23rd edition. Springer, 2005, p. 56 .
• G. Coriolis: Memoire sur les equations du mouvement relatif des systèmes de corps . In: Journal de l'École polytechnique . No. 15 , 1835, pp. 142–154 ( online [PDF]).
• Pierre Simon Laplace: Recherches sur plusieurs points du système du monde . In: Mémoires de l'Académie Royale des Sciences . tape 88 , 1775, pp. 75-182 ( online ). (For this source one should read footnote 12 in "A. Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics ".)
  
• Adrian Gill: Atmosphere-Ocean Dynamics (International Geophysics) . Academic Pr Inc, 1982, ISBN 0-12-283522-0 .
• Henry M. Stommel , Dennis W. Moore: An introduction to the Coriolis force. Columbia University Press, New York 1989, ISBN 0-231-06637-6 .
• AO Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics. Part I: A history to 1885. In: History of Meteorology. Volume 2, 2005, pp. 1-24.
• Halliday-Resnick-Walker: Halliday Physics. 2nd Edition. Wiley-VCH, 2009, p. 154 ff.

Web links

Commons : Coriolis force  - collection of images, videos and audio files

Wiktionary: Coriolis force  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Coriolis Force  - Learning and Teaching Materials

• Video: Coriolis and centrifugal force in the rotating frame of reference . Institute for Scientific Film (IWF) 2007, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / C-13095 .
• What is the Coriolis Force? from the alpha-Centauri television series(approx. 15 minutes). First broadcast on May 11, 2005.
• Video from Terra X
• Device for demonstrating the Coriolis force

Individual evidence

1. ↑ Coriolis Force, the. Duden online , accessed on November 30, 2013. In German, instead of the last syllable, the first i or the second o is usually stressed.
2. ↑ Coriolis and centrifugal force in the rotating reference system: Video from 3:00 to 3:30 and from 5:00.
3. ↑ Jürgen Dankert, Helga Dankert: Technical Mechanics . 6th edition. Vieweg-Teubner, 2011, ISBN 978-3-8348-1375-6 . In technical mechanics , the "Coriolis acceleration" is seen as part of the acceleration in the inertial system, namely as the acceleration that must be given to the moving body perpendicular to its direction of movement in order to prevent its deflection; for this it has the opposite sign.
4. ↑ Wolfgang Demtröder: Experimentalphysik 1 . 6th edition. Springer Spectrum, Berlin Heidelberg 2013, ISBN 978-3-642-25465-9 , p. 83 .
5. ^ Dieter Meschede : Gerthsen Physics . 25th edition. Springer, Heidelberg 2017, p. 43 ff .
6. ↑ Richard Feynman et al. a .: Lectures on physics . Vol. 1, pages 19–2 , the last two sentences of the chapter.
7. ↑ Jürgen Dankert and Helga Dankert: Technical Mechanics. Springer, 6th edition, 2011, p. 497.
8. ^ Richard Feynman: The Feynman Lectures on Physics . 3. Edition. tape 1 . Basic Books, 2010, ISBN 978-0-465-02414-8 , pp. 19-15-19-16 (English).
9. ↑ Brigitte Klose: Meteorology . Springer, Berlin / Heidelberg 2008, p. 207 .
10. ^ Lew Landau , Jewgeni Lifschitz : Mechanics . 3. Edition. Butterworth Heinemann, 1976, ISBN 978-0-7506-2896-9 , pp. 126-129 (English).
11. ↑ AO Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics. In: History of Meteorology. Volume 2, 2005, pp. 2-3.
12. ↑ E. Becker: Technical Thermodynamics: An introduction to thermo- and gas dynamics . BG Teubner, 1985, ISBN 978-3-519-03065-2 , pp. 185 .
13. ^ ^{A b} John Marshal, R. Alan Plumb: Atmosphere, Ocean, and Climate Dynamics: An Introductory Text. Academic Press, 2007, pp. 96-97. Google.
14. ↑ Anders Persson: The Coriolis Effect - a conflict between common sense and mathematics. Norrköping 2005, p. 13.
15. ^ John Marshall: Inertial circles - visualizing the Coriolis force: GFD VI. 2003.
16. ^ John Marshal, R. Alan Plumb: Atmosphere, Ocean, and Climate Dynamics: An Introductory Text . Academic Press, 2007, ISBN 978-0-12-558691-7 , pp. 101 ( google.com ).
17. ↑ Anders Persson: The Coriolis force on the physical earth. In: Weather. Vol. 55, 2000, pp. 234-239.
18. ↑ Slight fluctuations and very long-term changes in the angular velocity can be disregarded in most cases.
19. ↑ ^{a b c d} A. O. Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885 . In: History of Meteorology . tape 2 , 2005, p. 1–24 ( meteohistory.org [PDF]). meteohistory.org. ( Memento from April 11, 2014 in the Internet Archive ).
    
20. ^ Robert Wichard Pohl : Mechanics, acoustics and thermodynamics. 17th edition, Springer-Verlag Berlin, Heidelberg, New York 1969, p. 94.
21. ^ Robert Stewart: Introduction to Physical Oceanography . Orange Grove Texts Plus, 2009, pp. 311 ( online [PDF; accessed October 19, 2019]).
22. ↑ Anders Persson: The Coriolis force and the geostrophic wind. In: Weather. Vol. 56, 2001, pp. 267-272.
23. ^ ^{A b c} Anders Persson: The Coriolis force and drifting icebergs. In: Weather. Vol. 56, 2001, pp. 439-444.
24. ^ NASA : Ocean in motion: Ekman Transport.
25. ↑ Swedish Meteorological and Hydrological Institute : Surface temperatures in the central Pacific as a result of upwelling created by the Coriolis force
26. ↑ Christoph Drösser: Right? Strange vortex. On: zeit.de. May 12, 1997, accessed December 14, 2014.
27. ↑ Jearl Walker : The Flying Circus of Physics . Oldenbourg Wissenschaftsverlag, 2007, ISBN 978-3-486-58067-9 ( limited preview in Google book search).
28. ^ Norbert Lossau : Five minutes of physics: bathtubs and low pressure areas. In: The world . June 6, 2007.
29. ↑ Anders Persson: Is the Coriolis effect an 'optical illusion'? In: Quarterly Journal of the Royal Meteorological Society Volume 141, 2014, pp. 1957-1967.
30. ↑ Anders Persson: The obstructive Coriolis force. In: Weather. Vol. 56, 2001, pp. 204-209.
31. ^ ^{A b} Anders Persson: The Coriolis force and the nocturnal jet stream. In: Weather. Vol. 57, 2002, pp. 28-33.
32. ↑ In general, even with parallel isobars, the wind is not directed completely in a straight line, this only applies in the statistical sense, but rather it runs cycloidal, since a rotational movement is superimposed on the translation.
33. ↑ The frictional force does not have to be directed exactly against the wind direction due to internal friction in the air.
34. ^ Ernst Heyer: Weather and Climate. 3rd edition, BSB BGTeubner Verlagsgesellschaft Leipzig 1975, pp. 130-131.
35. ↑ Rossby Waves.
36. ^ ^{A b} Hermann Flohn : On the dididactics of the general circulation of the earth. In: Geographical Rundschau. Volume 12, 1960, pp. 129-142, 189-196.
37. ↑ Brigitte Klose: Meteorology . Springer, Berlin / Heidelberg 2008, p. 220 .
38. ↑ Anders Persson: Coriolis I. (Slide 20: Comparison of the Mersenne experiment with free fall using the area theorem .)
39. ↑ Roland Steffen: Industrial flow measurement: Coriolis force flow measurement. 2004.
40. ↑ Klaus-Dieter Sommer: Modern methods for measuring force, mass and quantities derived from them. University of Erlangen 2008 (with equations and device construction).
41. ↑ MEMS sensors at a glance, automotive electronics. ( Memento from May 23, 2013 in the Internet Archive ). (PDF; 2.8 MB), April 2007.
42. ↑ Detlef Billep: Modeling and simulation of a micromechanical rotation rate sensor. (PDF; 4.6 MB), dissertation.
43. ^ Kristian Silver: An Intuitive Approach to the Coriolis Effect. Uppsala 2011, pp. 34-43.
44. ↑ Anders Persson: Hadley's Principle. Part 1 . In: Weather. Volume pp. 335-338; Part 2. In: Weather. Volume 64 2009, pp. 44-48.
45. ↑ ^{a b} Anders Persson: Hadley's Principle. Part 3. In: Weather. Volume pp. 93-96
46. ^ AO Persson: The Coriolis Effect - a conflict between common sense and mathematics. The Swedish Meteorological and Hydrological Institute: 8. 2005, pp. 5-6.
47. ↑ ^{a b} A. O. Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics. In: History of Meteorology. Volume 2, 2005, p. 6.
48. ↑ AO Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics. In: History of Meteorology. Volume 2, 2005, p. 18.
49. ↑ In an earlier work by Leonhard Euler from 1750 the factor 2 was still missing in the formula (Giulio Maltese: On the relativity of motion in Leonhard Euler's science. In: Archive for history of exact sciences. Volume 54 (January 2000), Pp. 319-348, here p. 343).
50. ^ PS Laplace: Recherches sur plusieuers points du Système du Monde . In: Mém. Acad. roy . des Sciences . 88, 1775, pp. 75-182. Quoted in David Edgar Cartwright: Tides: A Scientific History. Cambridge 1999, limited preview in Google Book search.
51. ^ Johann Friedrich Benzenberg: Experiments on the law of the fall, on the resistance of the air and on the rotation of the earth, together with the history of all earlier attempts from Galilee to Guglielmi. Dortmund 1804, 2nd edition, Hamburg 1824.
52. ↑ Ferdinand Reich: Drop tests over the revolution of the earth: employed in the Brüderschachte near Freiberge. Freiberg 1832.
53. ↑ Jürgen Teichmann : Change of the world view (=  cultural history of the natural sciences and technology, edited by the Deutsches Museum Munich ). 2nd Edition. Wissenschaftliche Buchgesellschaft, Darmstadt 1983, pp. 157–159.
54. ↑ Presentation of Rundell's Experiment, Mechanics Magazine, May 1849 , and a letter from Oersted to Herschel in the reports of the British Association for the Advancement of Science, 1846.
55. ^ GG Coriolis: Memoire sur les equations du mouvement relatif des systèmes de corps . In: Journal de l'École polytechnique . 15, 1835, pp. 142-154. The preliminary work by Laplace (1775) is not mentioned in this publication.
56. ↑ Adolf Sprung : Studies on the wind and its relationship to air pressure. I. On the mechanics of air movements. In: Archive of the Deutsche Seewarte Volume 2, 1879, pp. 1–28.
57. ↑ AO Persson: The Coriolis Effect: Four centuries of conflict between common sense and mathematics. In: History of Meteorology. Volume 2, 2005, pp. 13-15.
58. ^ Karl Ernst von Baer: About a general law in the design of river beds. In: Caspian Studies. 1860, VIII, pp. 1-6.
59. ↑ Julius Bartels : Again the Baer law. In: Petermanns Geographische Mitteilungen . 68, vol. 1922, pp. 146-147.
60. ^ Adolf Schmidt : The distracting force of the rotation of the earth. In: Petermanns Geographische Mitteilungen. 68, vol. 1922, pp. 144-146.
61. ↑ Karl-Heinz Bernhardt : Tea cup cyclones and river meanders - Einstein classic. (PDF), 2005, pp. 81–95, here pp. 87–88.
62. ↑ Albert Einstein: The cause of the meander formation of the rivers and the so-called Baer's law. In: The natural sciences . Volume 14, 1926, pp. 223-224; Handwritten draft of the publication .
63. ↑ Einstein reported in Die Naturwissenschaften 1926 (p. 223) the view held by geographers of a stronger erosion force on the right bank of the river, without deriving it or taking part in the discussion about it.
64. ↑ Nikolai Braschman: Note concernant la pression des wagons sur les rails droits et des courants d'eau suer la rive droite du mouvement en vertu de la rotation de la terre. In: Comptes rendues. Volume 53, 1861, pp. 1068-1071.
65. ↑ Helmut Vogel: Problems from Physics. Exercises and solutions for the 17th edition of Gerthsen / Vogel Physik. Springer, Berlin 1993, ISBN 3-540-56632-5 , p. 40.
66. ↑ Anders Persson: The Coriolis force according to Coriolis. In: Weather. Vol. 56, 2001, pp. 439-444.