Foucault's pendulum

This article covers the experimental setup; for the novel of the same name by Umberto Eco, see The Foucault Pendulum .

The Foucault pendulum in the Paris Panthéon

Foucault's pendulum at the north pole of the rotating earth

A Foucault pendulum is a long, spherical pendulum with a large pendulum mass, with the help of which the earth's rotation can be detected without reference to observations in the sky .

Trials and description

On January 3, 1851, the French physicist Léon Foucault carried out an experiment in the basement of his house in which he made a two-meter-long pendulum swing close to the ground and precisely marked its path. He observed that the plane of oscillation of the pendulum turned slowly. The force of gravity, which only acts vertically, could not cause this rotation, and no other external force acted on the pendulum. So it wasn't the pendulum, but the ground (the earth ) that changed direction. Strictly speaking, the pendulum describes a narrow rosette orbit (see adjacent figure), with which the plane of oscillation of the pendulum rotates slowly relative to the ground.

On February 3, 1851, Foucault carried out the experiment in the Paris observatory with a 12 meter long pendulum. On March 26, 1851, he presented it to the public in the Panthéon with a 67-meter-long pendulum and a 28-kilogram pendulum body. At the lower end of the pendulum body was a point that marked a track in a bed of sand on the floor with each oscillation. This was a sensational proof of the earth's rotation suitable for laypeople. The Italian physicist Vincenzo Viviani made similar observations as early as 1661 , but he did not yet associate them with the Earth's rotation.

The experiments were repeated by Caspar Garthe in Cologne Cathedral and Friedrich Magnus Schwerd in Speyer Cathedral , but with results that were not quantitatively satisfactory. Heike Kamerlingh Onnes carried out more precise measurements as part of his dissertation from 1879 and pointed out the sources of error that had disturbed Cologne and Speyer. Foucault pendulums are still hanging in various natural science museums today . The iron ball of the original pendulum was kept in the Conservatoire National des Arts et Métiers until 1946 and then returned to the Panthéon.

The suspension of the pendulum can be elastic, cardanic or rigid. It must not transmit any torque to the pendulum over one oscillation, in order not to obscure the effect.

Explanation

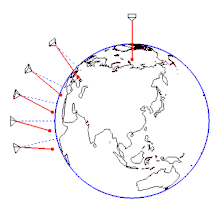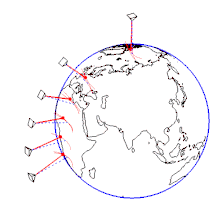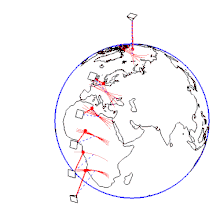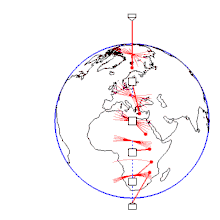
The physical explanation is that the main effect of the rotation of the earth is that the earth rotates away below the plane of oscillation of the pendulum, while the plane of oscillation itself remains unchanged. This is easiest to see at the North or South Pole , because the suspension point of the pendulum remains at rest there despite the rotation of the earth. Therefore the earth would turn under the pendulum exactly once in a sidereal day . (The four minutes difference to the exactly 24-hour sunny day results from the fact that the sun moves on in the starry sky.) The rotation observed on the pendulum is counter to the direction of the earth's rotation, i.e. clockwise at the north pole (i.e. clockwise), and left at the south pole. At the equator, on the other hand, the plane of oscillation of the pendulum does not rotate at all in relation to the ground. The closer you get to the poles, the stronger the rotation.

From the point of view of an observer who considers the earth to be at rest, the pendulum plane rotates in the manner described. In his reference system, this is due to an inertial force acting in addition to gravity . This is the Coriolis force , which in relation to the earth-fixed reference system always acts on it transversely to the direction of movement of the pendulum body and deflects it to the right in the northern hemisphere and to the left in the southern hemisphere . As a result, the plane of oscillation rotates around the vertical through the suspension point.

The angular velocity of this rotation is constant. It amounts to

${\displaystyle \omega _{\text{Coriolis}}=\Omega \,\sin(\varphi )}$,

where is the angular velocity of the earth and the latitude of the point of suspension. In Germany, a full rotation takes between 29.3 hours (in Flensburg) and 32.2 hours (in Munich). At the equator ( ) the plane of oscillation does not rotate at all. ${\displaystyle \Omega }$ ${\displaystyle \varphi }$ ${\displaystyle \varphi =0}$

Derivation of the rotational movement of the pendulum plane

Coordinate system used for the calculation

Path curve of a Foucault pendulum at a 1000 times faster earth rotation

Consider a mathematical pendulum at a location in the northern hemisphere with the latitude . An earth-fixed coordinate system is aligned in such a way that at the base of the pendulum it points to the east, to the north and to the zenith. The length of this pendulum should be much greater than its amplitude , so that, as a good approximation, applies to the body of the pendulum . The pendulum body thus remains in the xy-plane and experiences (through the acceleration of gravity ) the restoring force in a harmonic approximation ${\displaystyle \varphi }$ ${\displaystyle x,\,y,\,z}$ ${\displaystyle {\hat {e}}_{x}}$ ${\displaystyle {\hat {e}}_{y}}$ ${\displaystyle {\hat {e}}_{z}}$ ${\displaystyle l}$ ${\displaystyle A}$ ${\displaystyle z=0}$ ${\displaystyle g}$

${\displaystyle {\vec {F}}_{r}=-m\,{\frac {g}{l}}{\begin{pmatrix}x\\y\\0\end{pmatrix}}}$.

If the xy-plane represented an inertial system, then the pendulum would execute in it with a frequency of plane harmonic oscillations (see the relevant section in spherical pendulum ). Depending on the initial condition, this would be a linear oscillation through the base point or an ellipse or a circle around the base point, whereby the trajectory does not change on the xy plane. ${\displaystyle \textstyle \omega _{0}={\sqrt {g/l}}}$

The earth-fixed xyz coordinate system is not an inertial system; the earth rotates with angular velocity . (The effects due to the attraction of the moon and sun can be completely neglected.) The axis of rotation goes through the poles ( at both poles), which is the magnitude of the angular velocity . In order to calculate the movement in the co-rotating xyz reference system, the centrifugal force must be added to the linear restoring force ${\displaystyle {\vec {\Omega }}}$ ${\displaystyle \varphi =+90^{\circ }}$ ${\displaystyle \Omega =360^{\circ }/{\text{Siderischer Tag}}=2\pi /{(86164\,\mathrm {s} )\approx 7{,}3\cdot 10^{-5}\,\mathrm {s} ^{-1}}}$

${\displaystyle {\vec {F}}_{\text{Zf}}=-m\,{\vec {\Omega }}\times ({\vec {\Omega }}\times {\vec {R}})}$

and the Coriolis force

${\displaystyle {\vec {F}}_{\text{Cor}}=-2m\,{\vec {\Omega }}\times {\vec {v}}}$

add. ( is the position vector of the point (x, y, z), if the origin is in the center of the earth, its speed is in the fixed xyz reference system). ${\displaystyle {\vec {R}}}$ ${\displaystyle {\vec {v}}}$

The only practically observable change results from the fact that the entire trajectory turns with the angular velocity in the plane of oscillation around the vertical z-axis. In a reference system that rotates with the same angular velocity as compared to the fixed system, the pendulum maintains the orientation of its trajectory, i.e. i.e., it behaves like in an inertial frame. This is easiest to see for a pendulum whose rest position is the North Pole. There the earth simply rotates (counterclockwise) under the pendulum, which has no effect on the pendulum movement. (The same applies at the South Pole, but here with a clockwise rotation, because you have to use the geographical latitude as a variable for in the southern hemisphere in all formulas .) ${\displaystyle -\Omega \sin(\varphi )}$ ${\displaystyle \varphi }$ ${\displaystyle -\varphi }$

To make this understandable, note that angular velocity is a vector and can therefore be broken down into components (see figure):

${\displaystyle {\vec {\Omega }}=\Omega _{z}\,{\hat {e}}_{z}+\Omega _{y}\,{\hat {e}}_{y}={\begin{pmatrix}0\\\Omega _{y}\\\Omega _{z}\end{pmatrix}}}$

with and . ${\displaystyle \Omega _{z}=\Omega \sin(\varphi )}$ ${\displaystyle \Omega _{y}=\Omega \cos(\varphi )}$

For the Coriolis force, which is linear in , the effects of both components can be considered separately. The Coriolis force due to acts perpendicular to the z-axis, i.e. perpendicular to the plane of vibration. It just causes the observed rotation of the orientation of the trajectory. The Coriolis force due to has only a negligible effect, because it is vertical to the xy plane to which the body is bound, and its magnitude is at least a factor smaller than the vertical force of gravity. (The order of magnitude results from the maximum speed for the conditions in existing Foucault pendulums.) ${\displaystyle {\vec {\Omega }}}$ ${\displaystyle \Omega _{z}}$ ${\displaystyle \Omega _{y}}$ ${\displaystyle \textstyle \Omega /\omega _{0}\cdot A/l\approx 10^{-6}}$ ${\displaystyle v_{\mathrm {max} }=A\omega _{0}}$

The centrifugal force, on the other hand, depends on the square of . The static effect of centrifugal force leads to a deviation of the earth from the spherical shape ( earth flattening 21 km) and to a change in the direction and strength of the acceleration caused by gravity; these influences are already largely taken into account in the form of the measured values ​​for the parameters . Another influence on the period of oscillation and on the trajectory of the pendulum is negligible, because because of the quadratic dependence, the centrifugal force is at least a factor weaker than the restoring force . After this was once confirmed by exact calculations in the 19th century, the centrifugal force and other terms of the order of magnitude are consistently neglected in this context. ${\displaystyle {\vec {\Omega }}}$ ${\displaystyle g}$ ${\displaystyle \textstyle \Omega ^{2}/\omega _{0}^{2}\approx 10^{-8}}$ ${\displaystyle \Omega ^{2}/\omega _{0}^{2}}$

Calculation of the equations of the path

With the above justified neglect of the centrifugal force and the component of the Coriolis force caused by the equation of motion of the pendulum mass in the xy-plane reads: ${\displaystyle \Omega _{y}=\Omega \cos(\varphi )}$

${\displaystyle {\begin{pmatrix}{\ddot {x}}\\{\ddot {y}}\end{pmatrix}}=2\Omega _{z}{\begin{pmatrix}{\dot {y}}\\-{\dot {x}}\end{pmatrix}}-\omega _{0}^{2}{\begin{pmatrix}x\\y\end{pmatrix}}}$

These are two coupled ordinary differential equations of the second order. They become a single differential equation of the complex variable for easy solution

${\displaystyle u(t)=x(t)+\mathrm {i} \,y(t)}$

summarized:

${\displaystyle {\ddot {u}}=-2\mathrm {i} \Omega _{z}{\dot {u}}-\omega _{0}^{2}u}$

This has the form of a harmonic oscillation equation with an imaginary attenuator and can be solved directly with the methods known from there. Here, however, it is instructive, based on the considerations presented above, to express the movement in a coordinate system that rotates with the angular velocity in relation to the xy system . This is done through a variable transformation ${\displaystyle -\Omega _{z}}$

${\displaystyle u(t)=\mathrm {e} ^{-\mathrm {i} \Omega _{z}t}U(t)}$,

because the real and imaginary parts of form an XY coordinate system, which rotates in relation to the xy coordinate system with the angular velocity in the plane of vibration. Substituting for actually gives the simpler differential equation ${\displaystyle U(t)=X(t)+\mathrm {i} \,Y(t)}$ ${\displaystyle -\Omega _{z}}$ ${\displaystyle U(t)}$

${\displaystyle {\ddot {U}}=-(\omega _{0}^{2}+\Omega _{z}^{2})U}$.

This is the equation for a stationary undamped harmonic oscillation, but with the frequency

${\displaystyle \omega '=\omega _{0}{\sqrt {1+{\frac {\Omega _{z}^{2}}{\omega _{0}^{2}}}}}\approx \omega _{0}}$.

Accordingly, the coordinates describe the movement that a spherical pendulum would execute in the inertial system (see Harmonic Oscillator # Two-dimensional oscillator ). The term of the order of magnitude is consistently neglected in the treatment of the Coriolis force as well as in the treatment of the centrifugal force. In fact, both contributions approximately cancel each other out, since they come in with the opposite sign. The undisturbed oscillation of the pendulum with the undisturbed frequency is modulated in complex notation so an additional function , which means a uniform rotation around the z-axis. ${\displaystyle X(t),\,Y(t)}$ ${\displaystyle \Omega _{z}^{2}/\omega _{0}^{2}}$ ${\displaystyle \omega _{0}}$ ${\displaystyle e^{\pm \mathrm {i} \Omega _{z}t}}$

For another short solution in polar coordinates see e.g. B. Noble.

In practice, the initial condition in the fixed xy system is often set in such a way that the pendulum is released at a starting position with an initial speed of zero . Then the solutions for the movement are, again expressed in the earth-fixed xy coordinates: ${\displaystyle x_{0},y_{0}}$

${\displaystyle {\begin{aligned}x(t)&=x_{0}\cos(\omega _{0}t)\cos(\Omega _{z}t)+x_{0}{\frac {\Omega _{z}}{\omega _{0}}}\sin(\omega _{0}t)\sin(\Omega _{z}t)+y_{0}\cos(\omega _{0}t)\sin(\Omega _{z}t)-y_{0}{\frac {\Omega _{z}}{\omega _{0}}}\sin(\omega _{0}t)\cos(\Omega _{z}t)\\y(t)&=-x_{0}\cos(\omega _{0}t)\sin(\Omega _{z}t)+x_{0}{\frac {\Omega _{z}}{\omega _{0}}}\sin(\omega _{0}t)\cos(\Omega _{z}t)+y_{0}\cos(\omega _{0}t)\cos(\Omega _{z}t)+y_{0}{\frac {\Omega _{z}}{\omega _{0}}}\sin(\omega _{0}t)\sin(\Omega _{z}t)\end{aligned}}}$

Instead of the equation of motion given above, the trajectory fulfills a similar equation in which the deflection coefficient is replaced by . Since these coefficients differ only by the order of magnitude , the discrepancy for the size values ​​to be measured is irrelevant. ${\displaystyle -\omega _{0}^{2}}$ ${\displaystyle -(\omega _{0}^{2}-\Omega _{z}^{2})}$ ${\displaystyle 10^{-8}}$

Exactly the same trajectory is obtained if one uses a coordinate system that rotates around its axis with the angular velocity compared to the earth-fixed system (see graphic above) approximately like an inertial system. The simple inertia-free differential equation of a harmonic oscillator applies here. Its solution trajectories are ellipses with the limiting cases of a circle or a straight line. The earth's rotation is not noticeable in the system. Rotationally transformed into the earth-fixed system, the solution curve is transformed into the trajectory of Foucault's pendulum given above. The rotating reference system is not an inertial system. It is not fixed to the stars, but is sufficient for the calculation of Foucault's pendulum as an approximation for an inertial system. ${\displaystyle xyz}$ ${\displaystyle -\Omega \sin \Phi }$ ${\displaystyle z}$ ${\displaystyle xyz}$

To represent this movement of the pendulum body, the notation in plane polar coordinates is recommended . It then applies to the distance from the rest position ${\displaystyle \rho }$

${\displaystyle \rho ^{2}(t)=x^{2}(t)+y^{2}(t)=\rho _{0}^{2}\left(\cos ^{2}(\omega _{0}t)+{\frac {\Omega _{z}^{2}}{\omega _{0}^{2}}}\sin ^{2}(\omega _{0}t)\right)}$.

Two properties become clear in this: For results in the original harmonic oscillation in the inertial system. That is true at the equator. Secondly, it is shown that the Foucault pendulum, released from a starting point at a distance, follows a rosette orbit. The path does not lead exactly through the origin, but approaches it up to a fraction . The fact that in this case the pendulum does not go exactly through the rest position leads, due to the anharmonicity of the spherical pendulum, to a corruption of the rotation of the oscillation plane by a fraction , which is why excessive oscillation amplitudes must be avoided. ${\displaystyle \Omega _{z}=0}$ ${\displaystyle \rho _{0}}$ ${\displaystyle {\tfrac {\rho _{\text{min}}}{\rho _{0}}}={\tfrac {\Omega _{z}}{\omega _{0}}}}$ ${\displaystyle {\tfrac {\Delta \Omega }{\Omega _{z}}}=-{\tfrac {3}{8}}{\tfrac {\rho _{0}^{2}}{l^{2}}}}$

Six identical Foucault pendulums for 6 hours

The rotation of the apsidal line of the orbit per oscillation can go through

${\displaystyle \Delta \phi =\arctan \left({\frac {y\left({\tfrac {2\pi }{\omega _{0}}}\right)}{x\left({\tfrac {2\pi }{\omega _{0}}}\right)}}\right)-\arctan \left({\frac {y_{0}}{x_{0}}}\right)=-2\pi {\frac {\Omega _{z}}{\omega _{0}}}}$

be calculated. In the northern hemisphere, the Focault's pendulum (actually its approximate plane of oscillation; viewed from above) thus rotates clockwise, in the southern hemisphere counterclockwise (see animation on the right). A complete rotation of Foucault's pendulum takes time

${\displaystyle T={\frac {2\pi }{\Omega \,\sin \varphi }}}$.

In Germany the level of vibration rotates by around per hour . ${\displaystyle 11{,}5^{\circ }}$

gallery

• 

  Pendulum in the orangery in Kassel

• 

  Pendulum at the University of Koblenz

• 

  Pendulum in the Deutsches Museum, Munich

literature

• Ágoston Budó: Theoretical Mechanics . 4th edition. VEB Deutscher Verlag der Wissenschaften, Berlin 1967, § 25 The Foucault pendulum experiment, p. 122-126 .
• Reiner M. Dreizler, Cora S. Lüdde: Theoretical Physics 1: Theoretical Mechanics . Springer-Verlag, 2008, ISBN 3-540-70558-9 , pp. 311 ff .
• William Duncan MacMillan: On Foucault's Pendulum . In: American Journal of Mathematics . tape 37 , no. 1 , 1915, p. 95-106 , doi : 10.2307 / 2370259 , JSTOR : 2370259 .

Web links

Commons : Foucault's Pendulum  - collection of images, videos and audio files

• Technical description of the pendulum on the website of the University of Munich (with webcam)
• The Foucault Pendulum (1985) - film from the collection of the Federal Institute for Scientific Film (ÖWF) in the online archive of the Austrian Media Library

additions

1. ↑ In the animation, the earth rotates approx. 5000 times faster than in reality. Initial condition: The pendulum starts at maximum deflection without an initial speed relative to the earth. The otherwise often shown rosette orbit arises when the stationary pendulum is pushed out of its rest position.
2. ↑ Pendulum length: 50 m, location: northern latitude, Earth's rotation 1000 times faster than real. With the real value, the curve would appear as a filled circular area because the oscillation lines overlapped. Early rash: , initial velocity . This value allows the pendulum to pass the origin. : Amount of the angular velocity of the earth's rotation : Normal coordinate of the angular velocity vector of the earth's rotation at the pendulum location. Time span of the representation: Quarter-period of the oscillation plane rotation The curve depicts the solution of the differential equations . : squared natural angular frequency of the pendulum : amount of gravitational acceleration ${\displaystyle \varphi =50^{\circ }}$
   ${\displaystyle y_{0}=1{\text{ m}}}$ ${\displaystyle {\dot {x}}_{0}=\Omega _{z}y_{0}}$
   ${\displaystyle \Omega }$
   ${\displaystyle \Omega _{z}=\Omega \sin(\varphi )}$
   
   
   ${\displaystyle {\begin{pmatrix}{\ddot {x}}\\{\ddot {y}}\end{pmatrix}}=2\Omega _{z}{\begin{pmatrix}{\dot {y}}\\-{\dot {x}}\end{pmatrix}}-\omega _{0}^{2}{\begin{pmatrix}x\\y\end{pmatrix}}}$
   ${\displaystyle \omega _{0}^{2}=g/L}$
   ${\displaystyle g}$
3. ↑ Setup at 90 ° N, 50 ° N, 30 ° N, 15 ° N, 0 ° and 15 ° S. Representation of the earth's rotation in the star-fixed system. The ratio of the pendulum oscillation period to the duration of the earth's orbit (star day) is actually much smaller. Initial condition: All pendulums start simultaneously from a maximum parallel deflection to the east with no initial speed.

Individual evidence

1. ↑ Heike Kamerlingh Onnes: Nieuwe Bewijzen voor de aswenteling the aarde . Wolters, Groningen 1879, p. 1–312 (Dutch, gdz.sub.uni-goettingen.de [accessed on March 16, 2018] Title in German: “New evidence for the axis rotation of the earth”).
2. ^ History Of The Pantheon Paris. In: pantheonparis.com. Retrieved October 17, 2018 . 
3. ↑ ^{a b} A. Budo: Theoretical Mechanics . 4th edition. VEB Deutscher Verlag der Wissenschaften, Berlin 1967, § 24 Movements on the rotating earth, p. 119 .
4. ↑ P. Furtwängler: Mechanics of physical apparatus. In: F. Klein, C. Müller (Ed.): Encyclopedia of Mathematical Sciences. Vol. IV.2, Teubner, Leipzig 1904.
5. ^ William J. Noble: A Direct Treatment of the Foucault Pendulum . In: American Journal of Physics . No. 20 , 1952, pp. 334–336 (English, edu.tw [PDF]).
6. ↑ TJ I'A. Bromwich: On the Theory of Foucault's Pendulum, and of the Gyrostatic Pendulum . In: Proceedings of the London Mathematical Society . s2-13, no. 1 , 1914, p. 222-235 (English, wiley.com ).
7. ^ WS Kimball: The Foucault Pendulum Star Path and the n -Leaved Rose . In: American Journal of Physics . tape 13 , no. 5 , 1945, p. 271-277 , doi : 10.1119 / 1.1990726 (English).
8. ^ Roland Szostak: A permanently swinging Foucault pendulum for schools . In: PLUS LUCIS 2 / 2002-1 / 2003 . Mathematics and science lessons. S. 11–15 ( online [PDF; 160 kB ]).