Mathematical pendulum

Oscillation of a thread pendulum

The mathematical pendulum or plane pendulum is an idealized pendulum . In this case, a mass imagined to be point-shaped, which is suspended at a point by means of a massless pendulum rod, can oscillate back and forth in a vertical plane, with friction effects , in particular air resistance, being neglected. The plane pendulum is a special case of the spherical pendulum that can also move in other spatial directions. Since the movement of the pendulum body takes place on a vertical circle, it is also referred to as a circular pendulum , although it more often refers to the conical pendulum .

In practice, a mathematical pendulum can be approximated by using a rod that is as long and thin as possible or (if the deflection is less than 90 °) a thin thread and a pendulum that is as small and heavy as possible. The fact that the oscillation range ( amplitude ) only decreases noticeably after a large number of oscillations with this structure shows that the friction has only a minor influence.

Pendulums, which do not approximately fulfill the mentioned properties of the mathematical pendulum, can be described by the more complicated model of the physical pendulum .

The period of oscillation is independent of the mass of the vibrating body. In the case of small oscillations, the oscillation duration is almost independent of the size of the amplitude. Here the pendulum shows an almost harmonic oscillation , the period of which is determined exclusively by the length of the pendulum and the prevailing gravitational acceleration . The period of oscillation is extended to infinity the closer the amplitude gets to 180 °. Larger excitations lead to "rollover", so that the pendulum body moves periodically in a circle.

Mathematical description

Equation of motion

The restoring force is given by the tangential component of the weight force, which can be determined using a sine: ${\displaystyle F_{\mathrm {tan} }=F_{\mathrm {G} }\cdot \sin(\varphi )}$

On the basis of the forces, the equation of motion of the pendulum oscillation is set up below .

Due to the force of gravity ( , = acceleration due to gravity ), when a thread pendulum of the mass is deflected, a force is produced which acts tangentially to the circular pendulum path. The radial component does not play a role in the movement as it acts in the direction of the thread. Since the mathematical pendulum has only one degree of freedom , a scalar equation is sufficient. The amount of the restoring force increases with the deflection angle with respect to the rest position. The restoring force vector always points in the direction of the rest position, which is why there is a minus in the following equation: ${\displaystyle F_{\mathrm {G} }=mg}$ ${\displaystyle g}$ ${\displaystyle m}$ ${\displaystyle F_{\mathrm {tan} }(t)}$ ${\displaystyle \varphi }$ ${\displaystyle F_{\mathrm {tan} }}$

${\displaystyle F_{\mathrm {tan} }(t)=-mg\cdot \sin \left(\varphi (t)\right)}$

When looking at a swaying pendulum of thread, it becomes apparent that the speed decreases with increasing deflection and that the direction changes after reaching the apex. The change in speed means that the pendulum mass experiences an acceleration, more precisely a tangential acceleration takes place, since a circular movement path is present. According to Newton's 2nd law, the equation of motion reads :

${\displaystyle m\cdot a_{\mathrm {tan} }(t)=F_{\mathrm {tan} }(t)}$

The tangential acceleration can be expressed by the angular acceleration . ${\displaystyle {\ddot {\varphi }}}$

${\displaystyle a_{\mathrm {tan} }(t)=l\cdot {\ddot {\varphi }}(t)}$

In the case of undisturbed oscillation, the restoring force of the pendulum is the only external force. After changing and reducing the mass, a non-linear differential equation of the second order arises :

${\displaystyle m\cdot l\cdot {\ddot {\varphi }}(t)=-m\cdot g\cdot \sin \left(\varphi (t)\right)}$

${\displaystyle {\ddot {\varphi }}(t)+{\frac {g}{l}}\cdot \sin \left(\varphi (t)\right)=0}$

which can also be written as a system of two coupled differential equations of the first order with the help of the angular velocity : ${\displaystyle \omega }$

${\displaystyle {\dot {\varphi }}=\omega }$,

${\displaystyle {\dot {\omega }}=-{\frac {g}{l}}\sin \varphi }$.

Equation of motion in Cartesian coordinates

In addition to the equation of motion with the angle, there are other possible forms of description. The movement of the mathematical pendulum can also be formulated as a vector differential equation with Cartesian coordinates . A possible derivation is made using the Lagrange formalism with a Lagrange multiplier . The holonomic constraint is based on the idea that the length of the pendulum arm corresponds to the length of the position vector . Since the length of the pendulum arm is constant in a mathematical pendulum, the following must apply: ${\displaystyle \varphi }$ ${\displaystyle f(x,y)=0}$ ${\displaystyle l}$ ${\displaystyle l}$

${\displaystyle f(x,y)=x^{2}+y^{2}-l^{2}=0}$

The vector differential equation below is based on this holonomic constraint. The first term represents the centripetal acceleration and the second term the part of the acceleration due to gravity acting tangentially on the circular path. In this representation, the length of the pendulum arm is omitted in the differential equation. However, the initial values ​​are used to define which can be represented as a function of the initial values ​​of the angle and the angular velocity . ${\displaystyle l}$ ${\displaystyle l}$ ${\displaystyle \varphi }$ ${\displaystyle {\dot {\varphi }}}$

${\displaystyle {\begin{bmatrix}{\ddot {x}}\\{\ddot {y}}\end{bmatrix}}=\underbrace {-{\frac {{\dot {x}}^{2}+{\dot {y}}^{2}}{x^{2}+y^{2}}}\cdot {\begin{bmatrix}x\\y\end{bmatrix}}} _{\text{Zentripetalbeschleunigung}}\;\;\;\underbrace {-{\frac {gx}{x^{2}+y^{2}}}\cdot {\begin{bmatrix}-y\\x\end{bmatrix}}} _{\text{Tangentielle Erdbeschleunigung}}\quad ,\quad \underbrace {{\begin{bmatrix}x_{0}\\y_{0}\end{bmatrix}}=l\cdot {\begin{bmatrix}-\sin \varphi _{0}\\\cos \varphi _{0}\end{bmatrix}}\quad ,\quad {\begin{bmatrix}{\dot {x}}_{0}\\{\dot {y}}_{0}\end{bmatrix}}=-l{\dot {\varphi }}_{0}\cdot {\begin{bmatrix}\cos \varphi _{0}\\\sin \varphi _{0}\end{bmatrix}}} _{\text{Anfangswerte}}}$

Small amplitudes: harmonic oscillation

Small-angle approximation of the sine function: For is . ${\displaystyle \varphi \approx 0}$ ${\displaystyle \sin(\varphi )\approx \varphi }$

The small angle approximation applies to small angles :

${\displaystyle \sin(\varphi )\approx \varphi }$.

Substitution results in a linear differential equation of the second order of the general form , the general solution of which leads to the oscillation equation . ${\displaystyle {\ddot {x}}+\omega _{0}^{2}x=0\ }$ ${\displaystyle x(t)=u\,\sin(\omega _{0}t+\phi )}$

${\displaystyle {\ddot {\varphi }}(t)+{\frac {g}{l}}\cdot \varphi (t)=0}$

${\displaystyle \varphi (t)=\varphi _{\text{max}}\cdot \sin \left({\sqrt {\frac {g}{l}}}\cdot t+\alpha \right)}$

The angle denotes the amplitude and the zero phase angle at the point in time . In addition, the natural angular frequency and the associated period duration can be seen. ${\displaystyle \varphi _{\text{max}}}$ ${\displaystyle \alpha }$ ${\displaystyle t=0}$ ${\displaystyle \omega _{0}}$ ${\displaystyle T_{0}}$

${\displaystyle \omega _{0}={\sqrt {\frac {g}{l}}}}$

${\displaystyle T_{0}=2\pi {\sqrt {\frac {l}{g}}}}$

Exact solution

Dependence of the period on the maximum deflection angle θ _c .

Since pendulums are always deflected more than infinitesimally in reality , they behave non-linearly , i. H. Oscillations with a finite amplitude are anharmonic . The general differential equation cannot be solved in elementary terms and requires knowledge of elliptic integrals . With this the general solution for the period can be developed in a series:

${\displaystyle {\begin{aligned}T(\varphi _{\text{max}})&=T_{0}\sum _{n=0}^{\infty }\left({\frac {\left(2n\right)!}{\left(2^{n}n!\right)^{2}}}\right)^{2}\sin ^{2n}\left(\varphi _{\text{max}}/2\right)\\&=T_{0}\cdot \left(1+\left({\frac {1}{2}}\right)^{2}\cdot \sin ^{2}\left({\frac {\varphi _{\text{max}}}{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\cdot \sin ^{4}\left({\frac {\varphi _{\text{max}}}{2}}\right)+\dots \right)\end{aligned}}}$

Alternatively, the elliptical integral that occurs can also be evaluated using the arithmetic-geometric mean : ${\displaystyle M}$

${\displaystyle T(\varphi _{\text{max}})=T_{0}\cdot {\frac {1}{M\left(1,\cos {\frac {\varphi _{\text{max}}}{2}}\right)}}}$

In addition, the damping due to friction losses in a real pendulum is greater than zero, so that the deflections decrease approximately exponentially over time.

That the period does not depend on , but only on the ratio , can also be seen from a dimensional analysis, e.g. B. with Buckingham's Π-theorem . Only the numerical factor ( for small amplitudes, in the exact solution) cannot be determined in this way. ${\displaystyle m}$ ${\displaystyle l/g}$ ${\displaystyle 2\pi }$ ${\displaystyle \textstyle M\left(1,\cos {\tfrac {\hat {\varphi }}{2}}\right)}$

The angle as an explicit function of time with starting angle and (positive) starting speed is: ${\displaystyle \varphi }$ ${\displaystyle t}$ ${\displaystyle \varphi _{0}}$ ${\displaystyle {\hat {\omega }}}$

${\displaystyle \varphi (t)=2\operatorname {am} {\Bigg (}{\frac {2l\cdot \operatorname {F} {\Big (}{\frac {\varphi _{0}}{2}}{\Big |}{\frac {4g}{\xi }}{\Big )}-{\sqrt {l\cdot \xi }}\cdot t}{2l}}{\Bigg |}{\frac {4g}{\xi }}{\Bigg )}}$

with , where the Jacobi amplitude and the elliptic integral are of the 1st kind . In the case of a negative , the situation can simply be mirrored by reversing the sign of the starting angle. ${\displaystyle \xi =2g+l\cdot {\hat {\omega }}^{2}-2g\cdot \cos(\varphi _{0})}$ ${\displaystyle \operatorname {am} ()}$ ${\displaystyle \operatorname {F} ()}$ ${\displaystyle {\hat {\omega }}}$

Numerical solution

An approximate solution can be recursively calculated through numerical integration of the two first-order differential equations . With the simplest integration method ( Euler explicitly ) and the step size , the angular velocity results: ${\displaystyle h}$

${\displaystyle \omega _{k+1}=\omega _{k}-{\frac {g\cdot h}{l}}\cdot \sin \varphi _{k}\quad k=(0,1,2,\cdots ,k_{\text{max}})}$

The previously calculated angular velocity can be used for the angle:

${\displaystyle \varphi _{k+1}=\varphi _{k}+h\cdot \omega _{k+1}}$

The initial values ​​for angular velocity and angle are assigned to the index . ${\displaystyle k=0}$

The accuracy of the solution can be checked by simulating over several periods and adjusting the step size.

Conservation Laws

The law of conservation of energy in mechanics applies to the mathematical pendulum . The potential energy decreases on the way from the maximum deflection to the rest position . The weight force associated with it - more precisely: its tangential component - performs acceleration work, whereby the kinetic energy increases. After crossing the minimum, a component of the weight acts against the direction of movement. Lifting work is done.

${\displaystyle E_{\mathrm {pot} }+E_{\mathrm {kin} }={\text{konst.}}\,}$

The differential equation can also be derived from this:

${\displaystyle E_{\mathrm {pot} }=m\;g\;l\cdot (1-\cos \varphi )}$

${\displaystyle E_{\mathrm {kin} }={\frac {1}{2}}\cdot m\;(l\ {\dot {\varphi }})^{2}}$

The sum is constant over time, so

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}(E_{\mathrm {pot} }+E_{\mathrm {kin} })=0&=m\;g\;l\cdot \sin \varphi \cdot {\dot {\varphi }}+m\;l^{2}\cdot {\dot {\varphi }}\cdot {\ddot {\varphi }}\\&=m\;l^{2}\cdot {\dot {\varphi }}\cdot \left({\frac {g}{l}}\cdot \sin \varphi +{\ddot {\varphi }}\right)\end{aligned}}}$

This equation has two solutions:

1. ${\displaystyle {\dot {\varphi }}=0}$, there is no movement; this solution can be ignored here.
2. ${\displaystyle {\frac {g}{l}}\cdot \sin \varphi +{\ddot {\varphi }}=0}$ ; this solution is the same as the solution above.

Using the conservation of energy, the maximum speed of the pendulum mass after releasing the angle can be calculated: ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle \varphi }$

${\displaystyle v_{\mathrm {max} }={\sqrt {2\cdot g\ \cdot l\cdot (1-\cos \varphi )}}}$

The maximum speed is reached at the lowest point of the pendulum mass, i.e. H. when the thread is vertical.

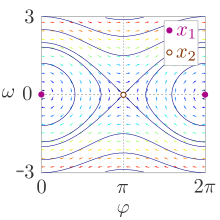
Equilibrium points in phase space

Phase space of the plane pendulum with g = l = 1. The phase space is periodic with period 2π with respect to the angle.

Equilibrium positions

The state of the system can be described by a tuple of the angle and the angular velocity . ${\displaystyle x=(\varphi ,\omega )}$ ${\displaystyle \varphi }$ ${\displaystyle \omega }$

There are two positions and where the system is in mechanical equilibrium . In both points the angular velocity and the sum of all acting forces and moments is zero. The equilibrium point at an angle of zero is the stable equilibrium when the pendulum has no deflection and speed. The second point is the unstable equilibrium when the pendulum has no speed and is "upside down". ${\displaystyle x_{1}=(0,0)}$ ${\displaystyle x_{2}=(\pi ,0)}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$

literature

• Ekbert Hering, Rolf Martin, Martin Stohrer: Physics for engineers . 8th edition. Springer, Berlin Heidelberg New York 2002, ISBN 3-540-42964-6 .

Web links

• A comprehensive analytical solution of the nonlinear pendulum , Karlheinz Ochs

Individual evidence

1. ↑ Physics and Mathematics with Maple, Kreispendel , accessed on December 22, 2014
2. ↑ Simon Tyran: The angle of a pendulum as an explicit function of time. 2016, p. 3 , accessed April 4, 2016 .