Anharmonic oscillator

The anharmonic oscillator is a physical system that can vibrate, in which the restoring force is not proportional to the deflection from the rest position. The consequence of this is that the oscillation is not strictly sinusoidal . Mechanical examples are pendulums (anharmonicity noticeable with greater deflection), tilting vibrations (the tilting of an upright object), and the hopping of a ball on a flat surface.

On closer inspection, almost all real oscillatory systems are anharmonic. Most, however, approach a harmonic oscillator the smaller the deflections from the rest position, because then the approximation of a linear restoring force always applies better (for mechanics see Hooke's law , mathematical pendulum ). In such anharmonic oscillators, small oscillations are approximately sinusoidal and have a certain natural frequency, the fundamental frequency of the oscillator.

Compared to the harmonic oscillator, fundamentally new phenomena occur with the anharmonic oscillator:

• The deviation from the sinusoidal shape means that the oscillation also contains harmonics (acoustic: overtones ) of the fundamental frequency.
• In the case of an asymmetrical law of force, the center of the oscillation shifts compared to the rest position. This occurs e.g. B. in the vibrations between the atoms of the solid body and is the cause of their thermal expansion.
• In the case of external excitation with a periodic force, the resulting forced oscillation has components with the frequency difference between the excitation frequency and the basic frequency and other integer combinations thereof. This is used for technical purposes. B. in non-linear optics with frequency doubling with laser light .
• In the case of external excitation with a periodic force, the anharmonic oscillator can also react with a chaotic movement if the initial conditions are selected accordingly or if its parameters are outside certain limits (e.g. if the damping is too low).

Equation of motion

Illustration of the anharmonic force law F (x) in example A (red) and B (green) for the case k = 1 and l = 0.2 , compared to the harmonic force law F (x) = - kx (blue). In addition, the associated potentials V (x) with F (x) = - d V / d x are shown in the gray box.

Trajectories of the harmonic oscillator and the two discussed anharmonic oscillators in comparison for the parameters m = k = 1, l = 0.2, c = 0 and different initial conditions and . The right column shows phase space portraits of the three oscillators. ${\displaystyle x(0)}$ ${\displaystyle m\cdot {\dot {x}}(0)=p(0)}$

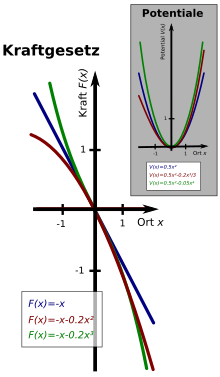
There are a number of different anharmonic oscillators and correspondingly many equations of motion. What they have in common is that their restoring force does not depend only linearly on the deflection , as is the case with the harmonic oscillator , but also on higher powers of ("non-linear force law"). In the figure opposite, the simplest examples are shown together with the approximate linear force law (blue straight line): ${\displaystyle F(x)=-kx}$ ${\displaystyle x}$ ${\displaystyle x}$

A) A simple asymmetrical force law (red curve in the picture on the right) reads . ${\displaystyle F(x)=-kx-lx^{2}}$

A transformation shows that the non-linear term increasingly weakens the restoring force on one side and strengthens it on the other, provided the deflections are not too large ( ). As you can see from the trajectories in the second figure, this leads to a stronger deflection of the oscillator in the direction of the weakened restoring force and to a slowed down period compared to the harmonic oscillator. Such an asymmetrical force law can be used as a second approximation (after the linear force law) to the Morse potential mentioned below in molecular physics . ${\displaystyle F(x)=-kx(1+{\tfrac {l}{k}}x)}$ ${\displaystyle |{\tfrac {l}{k}}x|<1}$ ${\displaystyle x(t)}$

B) A simple symmetrical force law (green curve in the picture on the right) reads . ${\displaystyle F(x)=-kx-lx^{3}}$

Depending on the sign of , the restoring force increases increasingly stronger ( ) or weaker ( ) compared to the harmonic oscillator . In the first case the oscillations occur faster with the same amplitude, in the second case more slowly. ${\displaystyle l}$ ${\displaystyle l>0}$ ${\displaystyle l<0}$

For example, this is the law of force for an approximation for the gravity or mathematical pendulum , whose period of oscillation increases with increasing amplitude. In this case the size stands for the dimensionless deflection angle of the pendulum. Such an approximation is obtained if one develops the restoring force of the mathematical pendulum in a Taylor series up to the third order in : ${\displaystyle l=-k/6}$ ${\displaystyle x}$ ${\displaystyle F(x)=-k\cdot \sin x}$ ${\displaystyle x}$

${\displaystyle F(x)=-k\cdot \sin x\approx \underbrace {-k\cdot x+{\frac {k}{6}}x^{3}} _{\text{1. und 3. Ordnung}}-{\frac {k}{120}}x^{5}+\ldots }$

The equations of motion with the damping term then result from Newton's law ${\displaystyle c{\dot {x}}}$

${\displaystyle m{\ddot {x}}=-c{\dot {x}}+F(x)}$

where the first and the second derivative of the function with respect to time denote: ${\displaystyle {\dot {x}}}$ ${\displaystyle {\ddot {x}}}$ ${\displaystyle x(t)}$ ${\displaystyle t}$

Case A : ${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx+lx^{2}=0}$

Case B : ${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx+lx^{3}=0}$

The linear force law and the differential equation of the damped harmonic oscillator are obtained for in both cases. Even for small deflections, the solution of the anharmonic oscillator is again almost harmonic, as the first trajectories in the figure on the right show. ${\displaystyle l=0}$

The superposition principle is invalidated by the non-linearity of the differential equations . This means that not every multiple of a solution is also a solution of the differential equation and, more generally, that with two solutions not every linear combination is also a solution (with arbitrary fixed numbers). The solution of the equation of motion is usually an elliptical integral and therefore cannot be represented in a closed form with elementary functions. This article focuses on periodic movements of the anharmonic oscillator. The attenuation is neglected in places, i.e. H. set. Only in this way, if no external force acts, will periodic movements in the strict sense result. For chaotic forms of movement, see chaos research and the specialist literature specified there. ${\displaystyle \alpha \cdot x(t)}$ ${\displaystyle x(t)}$ ${\displaystyle x_{1}(t),\;x_{2}(t)}$ ${\displaystyle x(t)=\alpha _{1}\cdot x_{1}(t)+\alpha _{2}\cdot x_{2}(t)}$ ${\displaystyle \alpha ,\,\alpha _{1},\,\alpha _{2}}$ ${\displaystyle c=0}$

Approximate solution

In the case of a weak anharmonic disturbance, i.e. H. or , the solution can be obtained by perturbation calculation . To do this, one gives an interference parameter in the form of a power series : ${\displaystyle |kx|\gg |lx^{2}|}$ ${\displaystyle |kx|\gg |lx^{3}|}$ ${\displaystyle x}$ ${\displaystyle \epsilon =-l/m}$

${\displaystyle {\begin{aligned}x(t)&=x_{0}(t)&+&\;\epsilon \cdot x_{1}(t)&+&\;\epsilon ^{2}\cdot x_{2}(t)&+&\ldots \\\omega &=\omega _{0}&+&\;\epsilon \cdot \omega _{1}&+&\;\epsilon ^{2}\cdot \omega _{2}&+&\ldots \end{aligned}}}$

The first term is the solution (adapted to the initial conditions) for the harmonic case , e.g. B. if the oscillator is currently released during the deflection with speed and has the basic frequency . ${\displaystyle l=0}$ ${\displaystyle x_{0}(t)=A\cos \omega _{0}t}$ ${\displaystyle t=0}$ ${\displaystyle x=A}$ ${\displaystyle {\dot {x}}=0}$ ${\displaystyle \omega _{0}={\sqrt {k/m}}}$

After inserting into the equation of motion, where is expressed by, there results a power series in , the coefficients of which are all to be set equal to zero. This gives differential equations for the individual approximation functions that have to be solved recursively. Concretely, the differential equation has the form of the equation of motion for a harmonic oscillator excited into forced oscillations by an external force given by the previous ones . ${\displaystyle x(t)}$ ${\displaystyle l}$ ${\displaystyle \epsilon }$ ${\displaystyle \epsilon }$ ${\displaystyle x_{i}(t)}$ ${\displaystyle x_{i+1}(t)}$ ${\displaystyle x_{i}}$

In case A follows in the first step

${\displaystyle x(t)=A\cos \omega _{0}t+\epsilon {\frac {A^{2}}{6\omega _{0}^{2}}}(3-4\cos \omega _{0}t+\cos 2\omega _{0}t)+\epsilon ^{2}(\ldots )+\ldots }$

The doubled basic frequency already occurs here. The mathematical reason for this can be traced back to the occurrence of the quadratic term in the equation of motion, which is linearized by the trigonometric identity . The further approximations result in summands with correspondingly higher multiples of the fundamental frequency, i.e. a whole spectrum of harmonics. ${\displaystyle x^{2}(t)}$ ${\displaystyle 2\cos ^{2}\phi =\cos(2\phi )+1}$

In case B , the first step is an unstable solution, because it contains a term that is too proportional. However, this can be eliminated if is set. In the first approximation, the oscillation frequency is dependent on the amplitude (as in case A only in the second step). ${\displaystyle x_{1}(t)}$ ${\displaystyle t\cos \omega _{0}t}$ ${\displaystyle \omega _{1}=-{\tfrac {3}{8}}{\tfrac {A^{2}}{\omega _{0}}}}$ ${\displaystyle \omega }$ ${\displaystyle A}$

Applications

Springs actually built into technical devices generally have a linear relationship between restoring force and deflection only within certain limits, sometimes also intended by the design. The dynamics of a system with such springs then follow the non-linear equations of motion as introduced above.

The Morse potential (blue) compared to the square potential of the harmonic oscillator (green). The energy levels are also shown which are equidistant ( ) for the harmonic oscillator, but which are less and less spaced with increasing energy with Morse code. ( is the binding energy, calculated from the minimum of the potential. Is the dissociation energy actually required to escape from the potential trough, because of the zero point energy ( ) is less than .) ${\displaystyle \hbar \omega }$ ${\displaystyle D_{e}}$ ${\displaystyle D_{0}}$ ${\displaystyle \nu =0}$ ${\displaystyle D_{e}}$

Important applications for anharmonic vibrations can be found in molecular physics for the vibration of diatomic molecules, or in solid-state physics for heat-induced vibrations of atoms. The anharmonicity is formed by the different effects when approaching (electrostatic repulsion, partially shielded by the electrons of the atomic shell , but reinforced by the Pauli principle ) and removal (restoring force due to the covalent bond of the atoms) of the atomic cores. As shown in the figure on the right, such oscillations can be calculated in a Morse potential .

Forced anharmonic vibrations

When moving under the influence of a time-dependent external force , anharmonic and harmonic oscillator are fundamentally different from each other. For example, even after the end of a transient process, the anharmonic oscillator can vibrate at different frequencies than those represented in the exciting force. Even with slow variations in the excitation frequency, sudden changes in the amplitude can occur. These phenomena are also of great practical interest, since real oscillators only behave in harmony as long as certain limits for deflection and / or frequency are observed. ${\displaystyle F(t)}$

These phenomena can generally be traced back to the non-linear form of the equation of motion, which means that the superposition principle can no longer be applied here. Some of the consequences:

• There is no generally valid solution method as with the forced oscillations of the harmonic oscillator. One has to integrate the equation of motion numerically or use analytical solutions that can only be obtained under approximate assumptions.
• The transient process (with periodic excitation) is not given by the superposition of the stationary oscillation with a free oscillation.
• The steady steady oscillation is not always independent of the initial conditions.
• After Fourier transformation, the equations of motion for different frequencies remain coupled to one another.

Amplitude jumps

As an example, consider the symmetrical force law (case B above ): The equation of motion reads (after division by , with and ): ${\displaystyle m}$ ${\displaystyle \gamma ={\frac {c}{2m}}}$ ${\displaystyle f(t)={\frac {F(t)}{m}}}$

${\displaystyle {\ddot {x}}+2\gamma {\dot {x}}+\omega _{0}^{2}x+\epsilon x^{3}=f(t)}$

Based on the assumption of a stationary harmonic oscillation

${\displaystyle x(t)=A\cdot \sin \Omega t}$

results from this for the causative force

(**) . ${\displaystyle \;f(t)=(\omega _{0}^{2}-\Omega ^{2})A\sin \Omega t\;+\;2\gamma \Omega A\cdot \cos \Omega t\;+\;\epsilon A^{3}\left({\tfrac {3}{4}}\sin \Omega t-{\tfrac {1}{4}}\sin(3\Omega t)\right)}$

The part of the force that oscillates with it comes from the deformation . This proportion is neglected in the following. The force can then be approximated ${\displaystyle 3\Omega }$ ${\displaystyle \sin ^{3}\phi \equiv {\tfrac {3}{4}}\sin \phi -{\tfrac {1}{4}}\sin(3\phi )}$

${\displaystyle f(t)=f_{0}\cdot \sin(\Omega t+\varphi )}$

summarize, so that here a force oscillating harmoniously with the frequency generates a harmonic oscillation of the same frequency. There is a phase shift and the amplitude of the force through ${\displaystyle \Omega }$ ${\displaystyle \varphi }$

${\displaystyle f_{0}^{2}=\left((\omega _{0}^{2}-\Omega ^{2})A\;+\;{\tfrac {3}{4}}\epsilon A^{3}\right)^{2}\;+\;4\,\gamma ^{2}\Omega ^{2}A^{2}}$

given. It is true that this equation cannot be changed in the form that is usual for the resonance curve. However, it can be resolved and the relationship between the excitation frequency and the stationary oscillation amplitude (for the force amplitude given by) is obtained in the form: ${\displaystyle A(\Omega )}$ ${\displaystyle \Omega ^{2}}$ ${\displaystyle \Omega }$ ${\displaystyle A}$ ${\displaystyle f_{0}}$

${\displaystyle (\Omega _{1/2})^{2}=\omega _{0}^{2}-2\gamma ^{2}\;+\;{\tfrac {3}{4}}\epsilon A^{2}\;\pm \;{\sqrt {{\frac {f_{0}^{2}}{A^{2}}}+\;4\,\gamma ^{2}\left(\gamma ^{2}\omega _{0}^{2}-{\tfrac {3}{4}}\epsilon A^{2}\right)}}}$.

The two solutions that arise here by solving a quadratic equation express that two excitation frequencies generally lead to the same amplitude of the stationary oscillation, as is the case with the harmonic oscillator on the left and right of the resonance peak. For the harmonic case ,, this formula agrees with the resonance curve of the harmonic forced vibrations, which has its amplitude maximum at and falls symmetrically on both sides. What is new with the anharmonic oscillator is that the resonance frequency shifts with increasing amplitude (term in the formula). As a result, the entire resonance peak in the diagram of the resonance curve can curve in such a way that it assumes an S-shape in certain frequency ranges, i.e. shows up to three different possible values ​​for the steady-state amplitude despite the same force amplitude and excitation frequency . If such a range is reached with slow, steady variation of the excitation frequency, the amplitude jumps from one branch of the resonance curve to another: the oscillation "tips". ${\displaystyle \Omega _{1/2}}$ ${\displaystyle \epsilon =0}$ ${\displaystyle \Omega ^{2}=\omega _{0}^{2}-2\gamma ^{2}}$ ${\displaystyle {\tfrac {3}{4}}\epsilon A^{2}}$ ${\displaystyle A(\Omega )}$ ${\displaystyle f_{0}}$ ${\displaystyle \Omega }$ ${\displaystyle A}$

Subharmonic excitation

In the previous section, a contribution to the force that oscillates with frequency was simply left out in equation (**). This is not always justified because this contribution can also play the main role under certain conditions. If that applies ${\displaystyle 3\Omega }$

${\displaystyle \gamma =0}$   and   , ${\displaystyle (\omega _{0}^{2}-\Omega ^{2})\;+\;{\frac {3}{4}}\epsilon A^{2}=0}$

then all with periodic terms vanish from equation (**) . It stays: ${\displaystyle \Omega }$

${\displaystyle x(t)=A\cdot \sin \Omega t}$

is a solution to external force

${\displaystyle f(t)=\epsilon A^{3}{\frac {1}{4}}\sin(3\Omega t)}$.

Example: The mathematical pendulum with basic frequency ( acceleration due to gravity, pendulum length), the law of force approximated by selecting the parameter , is driven by an external force ${\displaystyle \omega _{0}={\sqrt {g/L}}}$ ${\displaystyle g}$ ${\displaystyle L}$ ${\displaystyle \epsilon =-\omega _{0}^{2}/6}$

${\displaystyle F(t)=-{\frac {1}{24}}m\omega _{0}^{2}\cdot \sin(3\Omega t)\quad {\text{mit}}\quad \Omega ={\sqrt {7/8}}\omega _{0}}$.

Then it vibrates with amplitude and a three times reduced frequency like . In order to be able to observe this behavior, however, one must either meet the correct initial conditions or wait for additional natural vibrations to subside, which can take a long time due to the assumption of negligibly low damping. ${\displaystyle A=1\approx 57^{\circ }}$ ${\displaystyle x(t)=A\sin(\Omega t)}$

Intermodulation

Intermodulation describes the phenomenon that the oscillator responds to an excitation with two frequencies with an oscillation in which combination frequencies ( and integers) are also represented. During the transient process, which usually only lasts for a short time because of the damping, such frequency multiples and combination frequencies are also present in relation to the fundamental frequency . In acoustics, they can appear as audible tones, which are caused by the fact that the eardrum or a loudspeaker membrane is excited beyond the deflection up to which a linear law of force applies to the restoring force. ${\displaystyle \Omega _{1}\neq \Omega _{2}}$ ${\displaystyle \Omega =|n\Omega _{1}\;\pm \;m\Omega _{2}|}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle \omega _{0}}$

literature

Friedhelm Kuypers: Classic mechanics . 8th edition. Wiley-VCH, Weinheim 2007, ISBN 978-3-527-40721-7 .

See also

• Duffing oscillator
• Van der Pol system
• Method of harmonic balance
• Harmonic oscillator
• Harmonic oscillator (quantum mechanics)
• Perturbation theory (quantum mechanics)