Trajectory (mathematics)
In mathematics, the trajectory (also known as a trajectory) is usually the solution curve of a differential equation with given initial conditions. The differential equation describes the coordinates of a system (in phase space or spatial space) depending on a parameter, which in mechanical applications is usually time. Then the trajectory describes the coordinates of the system as a function of "time".
definition
We consider the solution of an initial value problem of the following form:
The solution of this initial value problem is assumed to be on a (maximum) existence interval .
The image is then used as a trajectory or phase curve of the system of equations
which is defined by this solution.
Phase space
The common representation of all trajectories of a system is called a phase portrait or phase space . The phase portrait thus contains all trajectories that provide the solutions to the initial value problems when the initial value passes through all values of the definition range.
example
The following system of linear differential equations is given:
A general solution of the system is the following linear combination:
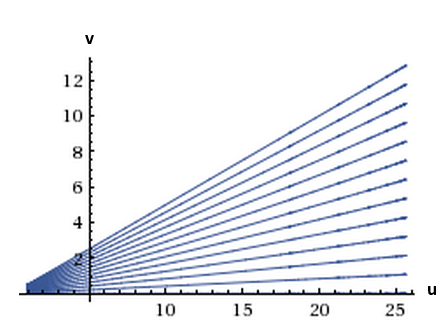
We want to draw trajectories for . The function to be represented can be found either by transforming the solutions for and or by solving the following differential equation ( and from the given differential equation):
The solution is:
The graph of this function is the trajectory sought, the constant is determined by the initial condition of the DGL system. A phase space consisting of twelve trajectories with different initial conditions is shown here.
Trajectories in Geometry
In geometry, the term trajectory is also used to designate a function graph that intersects a given set of curves isogonally , i.e. always at the same angle . If this angle is 90 °, one speaks of an orthogonal trajectory .
See also
Individual evidence
- ↑ See Brockhaus 1996. Vol. 22. p. 304