Orthogonal trajectory
An orthogonal trajectory is in math
- a curve that intersects all curves of a given set of curves (in the plane) perpendicularly.
For example, the orthogonal trajectories of a family of concentric circles are the straight lines through the center of the circles. The sub-area differential equation in mathematics provides suitable methods for finding orthogonal trajectories. In the standard procedure, you first determine an ordinary first-order differential equation for the orthogonal trajectories you are looking for and then solve this using the method separation of the variables . Both steps can be difficult or even impossible. Then you have to resort to numerical methods.
Orthogonal trajectories play z. B. in physics ( electrostatics ) a role as field lines in an electric field. They are perpendicular to the equipotential lines.
If any fixed angles are allowed when the curve intersects with the family of curves, an isogonal trajectory is obtained .
Determination of the orthogonal trajectories
In Cartesian coordinates
As a rule one assumes that the given family of curves is implicitly given by an equation of the form
- (0) 1st example 2nd example
is described, where is the flock parameter. If the family of curves is given explicitly in the form , it can also be described by implicitly. For the derivations required in the following, it is always tacitly assumed that they exist.
- Step 1
Implicit differentiation according to x results in
- (1) in the 1st example 2nd example
- 2nd step
It is now assumed that equation (0) can be solved for the parameter and thus can be eliminated from (1). A first order differential equation of the form is then created
- (2) in the 1st example 2nd example
which is fulfilled by the given set of curves.
- 3rd step
Since the slope of the orthogonal trajectory at the point must be the negative inverse of the slope of the given curve at this point, the differential equation applies to the orthogonal trajectory
- (3) in the 1st example 2nd example
- 4th step
This Dgl. one tries to solve it with one of the available methods.
In both examples, separation of the variables is appropriate. The solution
in the 1st example is the straight line and
in the 2nd example the ellipses
In polar coordinates
If the given set of curves is implicit in polar coordinates
- (0p)
before, as in the Cartesian case, the associated parameter-free Eq is determined.
- (1p)
- (2p)
the family of curves. The Dgl. the orthogonal ajectories in polar coordinates is then (see Heuser, p. 120)
- (3p)
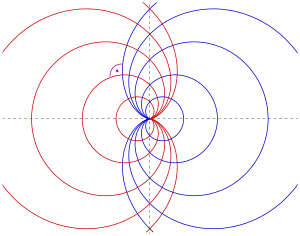
Example: cardioids :
- (0p) (in the picture: blue)
- (1p)
Elimination of results in the like. of the given family:
- (2p)
The Dgl. the orthogonal trajectories is then:
- (3p)
After solving this like. with separation of the changeable it finally results
This is the family of cardioids (red in the picture), which is created by mirroring the given family on the y-axis.
Isogonal trajectory
- A curve that intersects the curves of a given set of curves at a fixed angle is called an isogonal trajectory .
For an isogonal trajectory to the angle , the relationship between the slope of the curve (the family) and the slope of the trajectory is:
This follows from the addition theorem of the tangent, because the slope angle of the trajectory is larger than that of the given curve. The condition for the orthogonal trajectory results for.
To determine the isogonal trajectories of a family of curves, only the 3rd step in the above instructions needs to be adjusted.
- 3rd step (Isog.-Traj.)
The differential equation of the isogonal trajectory is:
- (3i)
In the 1st example , the angle of intersection is
- (3i)
This is a similarity differential equation , which with the substitution in a separable Eq. can be transferred and resolved. After back substitution one obtains the equation for the solution curves:
In polar coordinates this is simplified to
This equation describes logarithmic spirals (see picture).
Numerical methods
If the occurring differential equation of the trajectories cannot be solved with the theoretical method, one has to resort to numerical methods to solve an ordinary 1st order equation: z. B. on the Runge-Kutta method .
See also
literature
- R. Courant: Lectures on differential and integral calculus, Volume 2 , Springer-Verlag, 1963, p. 402.
- J. Erven, D. Schwägerl: Mathematics for engineers , Oldenbourg-Verlag, 2011, ISBN 978-3-486-59746-2 , p. 370.
- H. Heuser: Ordinary differential equations , Vieweg + Teubner, 2009, ISBN 978-3-8348-0705-2 , p. 120.
- K. Meyberg, P. Vachenauer: Höhere Mathematik 2 , Springer-Verlag, 2003, ISBN 978-3-540-41851-1 , p. 7.
- F. Paech: Analysis - descriptive and application-oriented , Fachbuchverlag, Leipzig, 2013, ISBN 978-3-446-43175-1 , p. 223.
Individual evidence
- ↑ Finckenstein, Lehn, Schellhaas, Wegmann: Workbook Mathematics for Engineers , Volume II, Teubner-Verlag, 2006, ISBN 3-8351-0030-0 , p. 14