Cardioids

Cardioids created by a rolling circle on a circle with the same radius.

Generation of a cardioid by rolling a circle on a circle with the same radius

The cardioid or heart curve (from Greek καρδία 'heart' ; English : cardioid) is a plane curve , more precisely an algebraic curve of the 4th order, which got its name because of its shape.

If one lets another circle with the same radius roll on the outside of a given solid circle with center M and radius  and one considers a certain point P on the rolling circle, then P describes a cardioid. The cardioid thus proves to be a special epicycloid . ${\displaystyle a}$

Cardioid equations

If the common radius of the generating circles with the centers , the roll angle and the zero point is the starting point (see picture), then one obtains the ${\displaystyle a}$ ${\displaystyle (-a,0),(a,0)}$ ${\displaystyle \varphi }$

• Parameter representation:

${\displaystyle x(\varphi )=2a(1-\cos \varphi )\cdot \cos \varphi \ ,}$

${\displaystyle y(\varphi )=2a(1-\cos \varphi )\cdot \sin \varphi \ ,\qquad 0\leq \varphi <2\pi }$ .

This results in the representation in

• Polar coordinates :

${\displaystyle r(\varphi )=2a(1-\cos \varphi )}$

With the substitution and the implicit representation in is obtained after removing the root ${\displaystyle \cos \varphi =x/r}$ ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$

• Cartesian coordinates :

${\displaystyle (x^{2}+y^{2})^{2}+4ax(x^{2}+y^{2})-4a^{2}y^{2}\,=\,0}$ .

Proof of the parametric representation

The proof of the parametric representation can easily be carried out with the help of complex numbers and their representation as a Gaussian number plane . The rolling motion of the black circle on the blue circle can be broken down into two consecutive rotations. The rotation of a point (complex number) around the zero point with the angle is caused by the multiplication with . ${\displaystyle z}$ ${\displaystyle 0}$ ${\displaystyle \varphi }$ ${\displaystyle e^{i\varphi }}$

The rotation around the point is . ${\displaystyle \Phi _{+}}$ ${\displaystyle a}$ ${\displaystyle z\mapsto a+(z-a)e^{i\varphi }}$

The rotation around the point is . ${\displaystyle \Phi _{-}}$ ${\displaystyle -a}$ ${\displaystyle z\mapsto -a+(z+a)e^{i\varphi }}$

A cardioid point is created by rotating the zero point by and then rotating it by the angle : ${\displaystyle p(\varphi )}$ ${\displaystyle a}$ ${\displaystyle -a}$ ${\displaystyle \varphi }$

${\displaystyle p(\varphi )=\Phi _{-}(\Phi _{+}(0))=\Phi _{-}(a-ae^{i\varphi })=-a+(a-ae^{i\varphi }+a)e^{i\varphi }=a\;(-e^{i2\varphi }+2e^{i\varphi }-1)}$.

from this it follows

${\displaystyle {\begin{array}{cclcccc}x(\varphi )&=&a\;(-\cos(2\varphi )+2\cos \varphi -1)&=&2a(1-\cos \varphi )\cdot \cos \varphi &&\\y(\varphi )&=&a\;(-\sin(2\varphi )+2\sin \varphi )&=&2a(1-\cos \varphi )\cdot \sin \varphi &.&\end{array}}}$

(The formulas were used. See the Trigonometry formula collection .) ${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi ,\ (\cos \varphi )^{2}+(\sin \varphi )^{2}=1,\ \cos 2\varphi =(\cos \varphi )^{2}-(\sin \varphi )^{2},\;\sin 2\varphi =2\sin \varphi \cos \varphi }$

Area, curve length and radius of curvature

For the above cardioid is

• the area , and ${\displaystyle A=6\pi a^{2}}$
• the curve length . ${\displaystyle L=16a}$
• Radius of curvature ${\displaystyle \rho (\varphi )={\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\ .}$

The evidence each uses the polar representation of the cardioids above. Formulas for the area and the curve length can be found e.g. B. here.

Proof of the area

${\displaystyle A=2\cdot {\tfrac {1}{2}}\int _{0}^{\pi }{(r(\varphi ))^{2}}\;d\varphi =\int _{0}^{\pi }{4a^{2}(1-\cos \varphi )^{2}}\;d\varphi =\cdots =4a^{2}\cdot {\tfrac {3}{2}}\pi =6\pi a^{2}}$ .

Proof of the curve length

${\displaystyle L=2\int _{0}^{\pi }{\sqrt {r(\varphi )^{2}+(r'(\varphi ))^{2}}}\;d\varphi =\cdots =8a\int _{0}^{\pi }{\sqrt {{\tfrac {1}{2}}(1-\cos \varphi )}}\;d\varphi =8a\int _{0}^{\pi }\sin({\tfrac {\varphi }{2}})d\varphi =16a}$ .

Proof of the radius of curvature

The radius of curvature of a curve in polar coordinates is (see curvature ) ${\displaystyle \rho }$ ${\displaystyle r=r(\varphi )}$

${\displaystyle \rho (\varphi )={\frac {\left[r(\varphi )^{2}+{\dot {r}}(\varphi )^{2}\right]^{3/2}}{r(\varphi )^{2}+2{\dot {r}}(\varphi )^{2}-r(\varphi ){\ddot {r}}(\varphi )}}\ .}$

For the cardioids it results ${\displaystyle r(\varphi )=2a(1-\cos \varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}}$

${\displaystyle \rho (\varphi )=\cdots ={\frac {[16a^{2}\sin ^{2}{\frac {\varphi }{2}}]^{\frac {3}{2}}}{24a^{2}\sin ^{2}{\frac {\varphi }{2}}}}={\frac {8}{3}}a\sin {\frac {\varphi }{2}}\ .}$

Properties of the cardioids

Tendons of a cardioid

Tendons through the tip

S1: The tendons through the tip of the cardioids are all the same length . ${\displaystyle 4a}$

S2: The centers of the tendons through the tip lie on the fixed generating circle (see picture).

Proof of S1

The points lie on a chord through the tip (= zero point). It is ${\displaystyle P:p(\varphi ),\;Q:p(\varphi +\pi )}$

${\displaystyle |PQ|=r(\varphi )+r(\varphi +\pi )}$

${\displaystyle =2a(1-\cos \varphi )+2a(1-\cos(\varphi +\pi ))=\cdots =4a}$ .

Proof of S2

The representation in the Gaussian plane of numbers (see above) is used for the proof. For the points

${\displaystyle P:p(\varphi )=a\;(-e^{i2\varphi }+2e^{i\varphi }-1)}$

${\displaystyle Q:p(\varphi +\pi )=a\;(-e^{i2(\varphi +\pi )}+2e^{i(\varphi +\pi )}-1)=a\;(-e^{i2\varphi }-2e^{i\varphi }-1)}$,

is

${\displaystyle M:{\tfrac {1}{2}}(p(\varphi )+p(\varphi +\pi ))=\cdots =-a-ae^{i2\varphi }}$

the center of the chord and lies on the circle of the Gaussian plane with center and radius (see picture). ${\displaystyle PQ}$ ${\displaystyle -a}$ ${\displaystyle a}$

The cardioid is created by mirroring a parabola on the unit circle (dashed)

Cardioids as the inverse curve of a parabola

→ Main article : Inversion (geometry)

• The cardioid is the image of a parabola under a circular reflection ( inversion ), in which the inversion center is in the focal point of the parabola (see picture).

In the example in the picture, the generator circles have the radius . The mirrored parabola satisfies the equation in xy coordinates . ${\displaystyle a={\tfrac {1}{2}}}$ ${\displaystyle x={\tfrac {1}{2}}(y^{2}-1)}$

Cardioids as the envelope of a group of circles

Cardioids as the envelope of a group of circles

If the tangents are mapped in the inversion of the parabola in the previous section, they merge as straight lines into a family of circles through the inversion center (zero point). A closer examination (recalculation) shows: The centers of the circles all lie on the fixed circle (cyan) of the cardioids. The circle of producers is the image of the guideline of the parabola. Since the tangents intersect perpendicularly on the guideline of a parabola and the mirroring of the circle is true to angle, circles of the group of circles also intersect perpendicularly on the generator circle.

The property of the circle set described here allows a simple method to draw a cardioid :

1) Choose a circle k and a point O on it,

2) draw circles through O with centers on k,

3) draw the envelope of these circles.

Proof with an envelope condition

It was through

${\displaystyle F(x,y,t)=0}$

given a family of implicit curves with the family parameter . The envelope (or envelope curve) consists of points that represent fixed solutions of the generally non-linear system of equations ${\displaystyle t}$ ${\displaystyle (x,y)}$ ${\displaystyle t}$

• ${\displaystyle F(x,y,t)=0,\quad F_{t}(x,y,t)=0\;.}$ (Envelope conditions)

are. ( means the partial derivative according to , see envelope ) ${\displaystyle F_{t}}$ ${\displaystyle t}$

Let k be the circle with center and radius . k has the parametric representation . The group of circles whose centers lie on k and which go through the point can be passed implicitly ${\displaystyle (-1,0)}$ ${\displaystyle 1}$ ${\displaystyle (-1+\cos t,\sin t)}$ ${\displaystyle O=(0,0)}$

${\displaystyle F(x,y,t)=(x+1-\cos t)^{2}+(y-\sin t)^{2}-(2-2\cos t)=0}$

describe. If you multiply the brackets, you get

${\displaystyle F(x,y,t)=x^{2}+y^{2}+2x\;(1-\cos t)-2y\;\sin t=0\;.}$ The 2nd set condition is

${\displaystyle F_{t}(x,y,t)=2x\;\sin t-2y\;\cos t=0}$

It is easy to check that the points of the cardioids with the parametric plot

${\displaystyle x(t)=2(1-\cos t)\cos t,\quad y(t)=2(1-\cos t)\sin t}$

satisfies the non-linear system of equations. The flock parameter here is identical to the angle parameter of the cardioids. ${\displaystyle t}$

Cardioids as the envelope of a set of straight lines

Cardioids as the envelope of a set of straight lines

A similarly simple method of constructing a cardioid as the envelope of a set of straight lines goes back to L. Cremona :

1. Draw a circle, divide it evenly with dots (see picture) and number them consecutively. ${\displaystyle 2N}$
2. Draw the tendons: . (You can put it this way: the second point on the chord moves at twice the speed.) ${\displaystyle (1,2),(2,4),....,(n,2n),....,(N,2N),(N+1,2),(N+2,4),....,}$
3. The envelope of these stretches is a cardioid.

Cardioids: Cremona production, for proof

proof

The trigonometric formulas for are used below . In order to keep the calculations simple, the proof for the cardioids is made with the polar representation (see section Cardioids with different orientation ). ${\displaystyle \cos \alpha +\cos \beta ,\ \sin \alpha +\sin \beta ,\ 1+\cos 2\alpha ,\ \cos 2\alpha ,\sin 2\alpha }$ ${\displaystyle r=2(1{\color {red}+}\cos \varphi )}$

Equation of tangent

to the cardioids with the polar representation : ${\displaystyle r=2(1+\cos \varphi )}$

From the parametric representation

${\displaystyle x(\varphi )=2(1+\cos \varphi )\cos \varphi ,}$

${\displaystyle y(\varphi )=2(1+\cos \varphi )\sin \varphi }$

one first calculates the normal vectors . The equation of the tangent is then: ${\displaystyle {\vec {n}}=({\dot {y}},-{\dot {x}})^{T}}$ ${\displaystyle {\dot {y}}(\varphi )\cdot (x-x(\varphi ))-{\dot {x}}(\varphi )\cdot (y-y(\varphi ))=0}$

${\displaystyle (\cos 2\varphi +\cos \varphi )\cdot x\ +\ (\sin 2\varphi +\sin \varphi )\cdot y=2(1+\cos \varphi )^{2}\ .}$

With the help of the trigonometric formulas and the subsequent division by , the equation of the tangent can be written as follows: ${\displaystyle \cos {\tfrac {1}{2}}\varphi }$

• ${\displaystyle \cos({\tfrac {3}{2}}\varphi )\cdot x+\sin({\tfrac {3}{2}}\varphi )\cdot y=4(\cos {\tfrac {1}{2}}\varphi )^{3}\quad 0<\varphi <2\pi ,\ \varphi \neq \pi .}$

Equation of the secant

to the circle with center and radius : For the equation of the secant through the two points we get: ${\displaystyle (1,0)}$ ${\displaystyle 3}$ ${\displaystyle (1+3\cos \theta ,3\sin \theta ),\ (1+3\cos {\color {red}2}\theta ,3\sin {\color {red}2}\theta ))}$

${\displaystyle (\sin \theta -\sin 2\theta )\cdot x\ +\ (\cos 2\theta -\sin \theta )\cdot y=-2\cos \theta -\sin 2\theta \ .}$

With the help of the trigonometric formulas and the subsequent division by , the equation of the secant can be written as follows: ${\displaystyle \sin {\tfrac {1}{2}}\theta }$

• ${\displaystyle \cos({\tfrac {3}{2}}\theta )\cdot x+\sin({\tfrac {3}{2}}\theta )\cdot y=4(\cos {\tfrac {1}{2}}\theta )^{3}\quad 0<\theta <2\pi .}$

The two angles have different meanings (see picture), but the result is the same straight line. So every above secant to the circle is also a tangent of the cardioids and ${\displaystyle \varphi ,\theta }$ ${\displaystyle \varphi =\theta }$

• the cardioid is the envelope of the circular tendons.

Note:
The proof can also be carried out with the envelope conditions of an implicit family of curves (see previous section). It describes

${\displaystyle F(x,y,t)=\cos {\tfrac {3}{2}}t\cdot x\ +\ \sin {\tfrac {3}{2}}t\cdot y-4(\cos {\tfrac {1}{2}}t)^{3}=0\ ,}$ the crowd of secants to the circle (see above)

${\displaystyle F_{t}(x,y,t)=-{\tfrac {3}{2}}\sin {\tfrac {3}{2}}t\cdot x\ +\ {\tfrac {3}{2}}\cos {\tfrac {3}{2}}t\cdot y+3\cos {\tfrac {1}{2}}t\sin t=0\ .}$

Both equations are straight line equations for fixed parameters t. The intersection

${\displaystyle x(t)=2(1+\cos t)\cos t,\quad y(t)=2(1+\cos t)\sin t}$

the straight line is a point of the cardioid with the polar representation . (Trigonometric formulas (see above) must be used again and again for transformations.) ${\displaystyle r=2(1+\cos t)}$

For cardioids as caustic :
light source , light beam , reflected beam ${\displaystyle Z}$ ${\displaystyle {\vec {s}}}$ ${\displaystyle {\vec {r}}}$

Cardioids as the caustic of a circle with a light source (right) on the circle

Cardioids as the caustic of a circle

The previous considerations also provide evidence that a cardioid occurs as the caustic of a circle with the light source on the circle.

• If light rays emanate from a point of a reflecting circle in the plane as shown in the figure, the light rays reflected inside the circle are the tangents of a cardioid. (see section cardioids in optics and acoustics ) ${\displaystyle Z}$

proof

The circle has (as in the previous section) the center and the radius . The circle then has the parametric representation ${\displaystyle (1,0)}$ ${\displaystyle 3}$

${\displaystyle k(\varphi )=(1+3\cos \varphi ,3\sin \varphi )\ .}$

The tangent in the circle point has the normal vector . The reflected beam must then have the normal vector (according to the illustration) and go through the point of the circle . The reflected beam is therefore (see previous section) on the straight line with the equation ${\displaystyle K=k(\varphi )}$ ${\displaystyle {\vec {n}}_{t}=(\cos \varphi ,\sin \varphi )^{T}}$ ${\displaystyle {\vec {n}}_{r}=(\cos {\color {red}{\tfrac {3}{2}}}\varphi ,\sin {\color {red}{\tfrac {3}{2}}}\varphi )^{T}}$ ${\displaystyle K:(1+3\cos \varphi ,3\sin \varphi )}$

${\displaystyle \cos {\tfrac {3}{2}}\varphi \cdot x\ +\ \sin {\tfrac {3}{2}}\varphi \cdot y=4(\cos {\tfrac {1}{2}}\varphi )^{3}\ ,}$

which in turn tangent to the cardioid with the polar representation

${\displaystyle r=2(1+\cos \varphi )}$

of the previous section.

Note: Multiple reflections on the circle are usually not taken into account in these considerations.

Cardioids as the base point curve of a circle

Cardioids: plumb points on circular tangents

The Cremona generation of a cardioid should not be confused with the following generation:

Let there be a circle and a fixed point on this circle. The following applies: ${\displaystyle k}$ ${\displaystyle O}$

• The plumb line from the point to the tangents of the circle form a cardioid. ${\displaystyle O}$ ${\displaystyle k}$

A cardioid is thus a special Fußpunktkurve (ger .: pedal curve ) of a circle.

proof

In the xy-plane the circle has the center and the radius . The tangent in the circle point has the equation ${\displaystyle k}$ ${\displaystyle (2a,0)}$ ${\displaystyle 2a}$ ${\displaystyle (2a+2a\cos \varphi ,2a\sin \varphi )}$

${\displaystyle (x-2a)\cdot \cos \varphi +y\cdot \sin \varphi =2a\ .}$

The perpendicular to the tangent is the point with the still unknown distance from the zero point . Insertion into the tangent equation gives ${\displaystyle O}$ ${\displaystyle (r\cos \varphi ,r\sin \varphi )}$ ${\displaystyle r}$ ${\displaystyle O}$

${\displaystyle (r\cos \varphi -2a)\cos \varphi +r\sin ^{2}\varphi =2a\quad \rightarrow \quad r=2a(1+\cos \varphi )}$

the polar representation of a cardioid.

Note: If the point is not on the circle , a Pascal snail is created (see next section). ${\displaystyle O}$ ${\displaystyle k}$

Cardioids as a Pascal snail

A Pascal snail is a flat curve with a polar representation . In the case of a cardioid results. So: ${\displaystyle r=b+a\cos t}$ ${\displaystyle b=a}$

• The cardioid is a special case of the Pascal snail , which in turn is a special case of the conchoid .

Cardioids on the glaze of a Dutch oven

Cardioids in optics and acoustics

• The appearance of light ( caustic ) in a coffee cup that is struck by light from a light source placed on the edge of the cup is a cardioid. The caustic, which is produced by parallel incident light, is, however, described by a different curve ( nephroids ); in other cases a mixed form arises.

In sound engineering , the polar diagram of the directional characteristic of a cardioid is called a kidney , even if it represents a heart curve.

Evolute of a cardioid

Evolute (green) of a cardioid (red)
magenta: a point P, its center of curvature M and the associated circle of curvature

The evolute of a plane curve is the geometric location of all centers of curvature of this curve. For a parameterized curve with a radius of curvature , the Evolute has the parametric representation ${\displaystyle {\vec {x}}(s)={\vec {c}}(s)}$ ${\displaystyle \rho (s)}$

${\displaystyle {\vec {X}}(s)={\vec {c}}(s)+\rho (s){\vec {n}}(s).}$

where is the appropriately oriented unit normal. ( points towards the center of curvature.) ${\displaystyle {\vec {n}}(s)}$ ${\displaystyle {\vec {n}}(s)}$

The following applies to a cardioid:

• The evolution of a cardioid is again a third as large (see picture).

proof

For the cardioids with the parametric display

${\displaystyle x(\varphi )=2a(1-\cos \varphi )\cos \varphi =4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi \ ,}$

${\displaystyle y(\varphi )=2a(1-\cos \varphi )\sin \varphi =4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi }$

is the unit normal

${\displaystyle {\vec {n}}(\varphi )=(-\sin {\tfrac {3}{2}}\varphi ,\cos {\tfrac {3}{2}}\varphi )}$

and the radius of curvature (see above)

${\displaystyle \rho (\varphi )={\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\ .}$

So the Evolute has the parametric representation

${\displaystyle X(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \sin {\tfrac {3}{2}}\varphi =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\cos \varphi -{\tfrac {4}{3}}a\ ,}$

${\displaystyle Y(\varphi )=4a\sin ^{2}{\tfrac {\varphi }{2}}\sin \varphi +{\tfrac {8}{3}}a\sin {\tfrac {\varphi }{2}}\cdot \cos {\tfrac {3}{2}}\varphi \ =\cdots ={\tfrac {4}{3}}a\cos ^{2}{\tfrac {\varphi }{2}}\sin \varphi \ .}$

These equations describe a cardioid that is one-third the size of the given cardioid, rotated 180 degrees, and shifted along the x-axis. ${\displaystyle -{\tfrac {4}{3}}a}$

( Trigonometric formulas were used:. ) ${\displaystyle \sin {\tfrac {3}{2}}\varphi =\sin {\tfrac {\varphi }{2}}\cos \varphi +\cos {\tfrac {\varphi }{2}}\sin \varphi \ ,\ \cos {\tfrac {3}{2}}\varphi =\cdots ,\ \sin \varphi =2\sin {\tfrac {\varphi }{2}}\cos {\tfrac {\varphi }{2}}\ ,\ \cos \varphi =\cdots }$

Orthogonal trajectories

orthogonal cardioids

An orthogonal trajectory of a family of curves is a curve that perpendicularly intersects each curve of the family. The following applies to cardioids:

• The orthogonal trajectories of the family of cardioids with the equations

${\displaystyle r=2a(1-\cos \varphi )\ ,\;a>0\ ,\ }$

are the cardioids with the equations

${\displaystyle r=2b(1+\cos \varphi )\ ,\;b>0\ .}$

(The second set is created by mirroring the first on the y-axis. See picture.)

Proof:
If a curve in polar coordinates is given by a function , the following relationship exists between the Cartesian coordinates and the polar coordinates of a point: ${\displaystyle r(\varphi )}$

${\displaystyle x(\varphi )=r(\varphi )\cos \varphi \ ,\qquad }$ ${\displaystyle y(\varphi )=r(\varphi )\sin \varphi \qquad }$

and thus

${\displaystyle {\frac {dx}{d\varphi }}=r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi \ ,\qquad }$ ${\displaystyle {\frac {dy}{d\varphi }}=r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi \ .}$

If you divide the last two equations you get the slope in Cartesian coordinates:

${\displaystyle {\frac {dy}{dx}}={\frac {r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi }{r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi }}.}$

For the cardioids with the equations or results ${\displaystyle r=2a(1-\cos \varphi )\;}$ ${\displaystyle r=2b(1+\cos \varphi )\ }$

${\displaystyle {\frac {dy_{a}}{dx}}={\frac {\cos \varphi -\cos 2\varphi }{\sin 2\varphi -\sin \varphi }}\quad }$ or. ${\displaystyle \quad {\frac {dy_{b}}{dx}}=-{\frac {\cos \varphi +\cos 2\varphi }{\sin 2\varphi +\sin \varphi }}\ .}$

(The gradients only depend on and no longer on the parameters  !) This results in ${\displaystyle \varphi }$ ${\displaystyle a,b}$

${\displaystyle {\frac {dy_{a}}{dx}}\cdot {\frac {dy_{b}}{dx}}=\cdots =-{\frac {\cos ^{2}\varphi -\cos ^{2}2\varphi }{\sin ^{2}2\varphi -\sin ^{2}\varphi }}=-{\frac {-1+\cos ^{2}\varphi +1-\cos ^{2}2\varphi }{\sin ^{2}2\varphi -\sin ^{2}\varphi }}=-1\ .}$

I.e. every curve of one group intersects every curve of the other group perpendicularly.

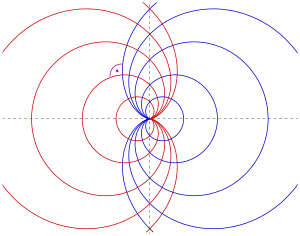
4 cardioids with polar representation and position in the coordinate system

Different orientated cardioids

If you choose other positions of the cardioids in the coordinate system, the equations that describe them change. The picture shows the 4 common orientations and their associated polar representations.

On the history of the cardioids

In search of an optimal form of gears, Ole Roemer examined epicycloids and thus cardioids in 1674. The name cardioid was first used by Johann Francesco Melchiore Salvemini Castillon . The length of a cardioid was calculated by Philippe de la Hire in 1708 . A cardioid is a special Pascal snail named after Étienne Pascal , the father of Blaise Pascal .

literature

• Small encyclopedia of mathematics . Harri Deutsch-Verlag, 1977, ISBN 3-87144-323-9 , p. 479

Web links

Commons : Cardioids  - collection of images, videos and audio files

Wiktionary: Cardioids  - explanations of meanings, word origins, synonyms, translations

• Eric W. Weisstein : Cardioid . In: MathWorld (English).
• John J. O'Connor, Edmund F. Robertson :  Cardioid. In: MacTutor History of Mathematics archive .
• Xah Lee: Cardioid (English)
• Curves & Surfaces: Cardioid . (English)
• Cardioid . Mathcurve

Individual evidence

1. ^ Meyberg, Vachenauer: Higher Mathematics 1 . Springer-Verlag, 1995, ISBN 3-540-59188-5 , pp. 198,199