Nephroids

Construction of a nephroid by rolling a circle on a circle with a double radius

Construction of the same nephroids by rolling a circle around a half-radius circle

A nephroid (from ancient Greek ὁ νεφρός ho nephros , "the kidney", according to its shape) is an algebraic curve of the 6th degree. The nephroids are created by rolling a circle with the radius on the outside of a circle with the radius . The nephroids thus belong to the epicycloid class . ${\displaystyle a}$ ${\displaystyle 2a}$

Equations of a nephroid

Nephroids: definition

If the radius of the small (rolling) circle and the center and radius of the large (fixed) circle, the roll angle (of the small circle) and the point are the starting point (see picture), then you get the ${\displaystyle a}$ ${\displaystyle (0,0),\;2a}$ ${\displaystyle 2\varphi }$ ${\displaystyle (2a,0)}$

• Parameter representation:

${\displaystyle x(\varphi )=3a\cos \varphi -a\cos 3\varphi =6a\cos \varphi -4a\cos ^{3}\varphi \ ,}$

${\displaystyle y(\varphi )=3a\sin \varphi -a\sin 3\varphi =4a\sin ^{3}\varphi \ ,\qquad 0\leq \varphi <2\pi }$ .

Substituting the parametric representation into the equation

• ${\displaystyle (x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}.}$

proves that it is the corresponding implicit representation.

Proof of the parametric representation

The proof of the parametric representation can easily be carried out with the help of complex numbers and their representation as a Gaussian number plane . The rolling motion of the black circle on the blue circle can be broken down into two consecutive rotations. The rotation of a point (complex number) around the zero point with the angle is caused by the multiplication with . ${\displaystyle z}$ ${\displaystyle 0}$ ${\displaystyle \varphi }$ ${\displaystyle e^{i\varphi }}$

The rotation about the point by the angle is . ${\displaystyle \Phi _{3}}$ ${\displaystyle 3a}$ ${\displaystyle 2\varphi }$ ${\displaystyle z\mapsto 3a+(z-3a)e^{i2\varphi }}$

The rotation about the point by the angle is . ${\displaystyle \Phi _{0}}$ ${\displaystyle 0}$ ${\displaystyle \varphi }$ ${\displaystyle z\mapsto ze^{i\varphi }}$

A nephroid point is created by rotating the point with and then rotating with : ${\displaystyle p(\varphi )}$ ${\displaystyle 2a}$ ${\displaystyle \Phi _{3}}$ ${\displaystyle \Phi _{0}}$

${\displaystyle p(\varphi )=\Phi _{0}(\Phi _{3}(2a))=\Phi _{0}(3a-ae^{i2\varphi })=(3a-ae^{i2\varphi })e^{i\varphi }=3ae^{i\varphi }-ae^{i3\varphi }}$.

From this it follows

${\displaystyle {\begin{array}{cclcccc}x(\varphi )&=&3a\cos \varphi -a\cos 3\varphi &=&6a\cos \varphi -4a\cos ^{3}\varphi \ ,&&\\y(\varphi )&=&3a\sin \varphi -a\sin 3\varphi &=&4a\sin ^{3}\varphi &.&\end{array}}}$

(The formulas were used. See the Trigonometry formula collection .) ${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi ,\ \cos ^{2}\varphi +\sin ^{2}\varphi =1,\ \cos 3\varphi =4\cos ^{3}\varphi -3\cos \varphi ,\;\sin 3\varphi =3\sin \varphi -4\sin ^{3}\varphi }$

Proof of the implicit representation

With results ${\displaystyle x^{2}+y^{2}-4a^{2}=(3a\cos \varphi -a\cos 3\varphi )^{2}+(3a\sin \varphi -a\sin 3\varphi )^{2}-4a^{2}=\cdots =6a^{2}(1-\cos 2\varphi )=12a^{2}\sin ^{2}\varphi }$

${\displaystyle (x^{2}+y^{2}-4a^{2})^{3}=(12a^{2})^{3}\sin ^{6}\varphi =108a^{4}(4a\sin ^{3}\varphi )^{2}=108a^{4}y^{2}\ .}$

different orientation

If the tips are on the y-axis:
Parametric display:

${\displaystyle x=3a\cos \varphi +a\cos 3\varphi ,\quad y=3a\sin \varphi +a\sin 3\varphi ).}$

Equation:

${\displaystyle (x^{2}+y^{2}-4a^{2})^{3}=108a^{4}x^{2}.}$

A shortened nephroid

Area, curve length and radius of curvature

For the above nephroids is

• the curve length , and ${\displaystyle L=24a}$
• the area ${\displaystyle A=12\pi a^{2}\ .}$
• the radius of curvature ${\displaystyle \rho (\varphi )=|3a\sin \varphi |.}$

The evidence uses parametric representation

${\displaystyle x(\varphi )=6a\cos \varphi -4a\cos ^{3}\varphi \ ,}$

${\displaystyle y(\varphi )=4a\sin ^{3}\varphi }$

of the above nephroids and their derivatives

${\displaystyle {\dot {x}}=-6a\sin \varphi (1-2\cos ^{2}\varphi )\ ,\quad \ {\ddot {x}}=-6a\cos \varphi (5-6\cos ^{2}\varphi )\ ,}$

${\displaystyle {\dot {y}}=12a\sin ^{2}\varphi \cos \varphi \quad ,\quad \quad \quad \quad {\ddot {y}}=12a\sin \varphi (3\cos ^{2}\varphi -1)\ .}$

Formulas for the area and the curve length can be found e.g. B. here.

Proof of the curve length

The formula for the length of a parameterized curve results in

${\displaystyle L=2\int _{0}^{\pi }{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}\;d\varphi =\cdots =12a\int _{0}^{\pi }\sin \varphi \;d\varphi =24a}$ .

Proof of the area (with the Leibniz sector formula )

${\displaystyle A=2\cdot {\tfrac {1}{2}}|\int _{0}^{\pi }[x{\dot {y}}-y{\dot {x}}]\;d\varphi |=\cdots =24a^{2}\int _{0}^{\pi }\sin ^{2}\varphi \;d\varphi =12\pi a^{2}}$ .

Proof of the radius of curvature

${\displaystyle \rho =\left|{\frac {\left({{\dot {x}}^{2}+{\dot {y}}^{2}}\right)^{\frac {3}{2}}}{{\dot {x}}{\ddot {y}}-{\dot {y}}{\ddot {x}}}}\right|=\cdots =|3a\sin \varphi |.}$

Nephroids as envelopes of a group of circles

Nephroids as envelopes of a group of circles

The following applies:

• If a circle and points are of the same diameter , then the envelope of the family of circles, the centers of which lie on top of and touch the diameter , is a nephroid with the tips . ${\displaystyle k_{0}}$ ${\displaystyle D_{1}D_{2}}$ ${\displaystyle d_{12}}$ ${\displaystyle k_{0}}$ ${\displaystyle d_{12}}$ ${\displaystyle D_{1},D_{2}}$

proof

Let it be the circle with the center and the radius . The necessary diameter is on the x-axis (see picture). The circle group is: ${\displaystyle k_{0}}$ ${\displaystyle (2a\cos \varphi ,2a\sin \varphi )}$ ${\displaystyle (0,0)}$ ${\displaystyle 2a}$

${\displaystyle f(x,y,\varphi )=(x-2a\cos \varphi )^{2}+(y-2a\sin \varphi )^{2}-(2a\sin \varphi )^{2}=0\ .}$

The envelope condition is

${\displaystyle f_{\varphi }(x,y,\varphi )=2a(x\sin \varphi -y\cos \varphi -2a\cos \varphi \sin \varphi )=0\ .}$

One calculates that the nephroid point fulfills the two equations and is thus a point of the envelope of the group of circles. ${\displaystyle p(\varphi )=(6a\cos \varphi -4a\cos ^{3}\varphi \;,\;4a\sin ^{3}\varphi )}$ ${\displaystyle f(x,y,\varphi )=0,\;f_{\varphi }(x,y,\varphi )=0}$

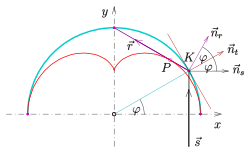
Nephroids as the envelope of a family of straight lines: The tangents of the nephroids are chords of a circle. The chords each run between point n and point 3n on the circular path, which is evenly divided into a number of steps that corresponds to a multiple of 3.

Nephroids as the envelope of a family of straight lines: The tangents of the nephroids are chords of a circle

Nephroids as the envelope of a set of straight lines

Similar to the creation of a cardioid as the envelope of a family of lines, the following applies here:

1. Draw a circle, divide it evenly with dots (see picture) and number them consecutively. ${\displaystyle 3N}$
2. Draw the tendons: . (You can put it this way: the second point on the tendon moves at three times the speed.) ${\displaystyle (1,3),(2,6),....,(n,3n),....,(N,3N),(N+1,3),(N+2,6),....,}$
3. The envelope of these stretches is a nephroid.

proof

The trigonometric formulas for are used below . To keep the calculations simple, the proof for the nephroids is made with the tips on the y-axis. ${\displaystyle \cos \alpha +\cos \beta ,\ \sin \alpha +\sin \beta ,\ \cos(\alpha +\beta ),\ \cos 2\alpha }$

Equation of tangent

to the nephroids with the parametric representation

${\displaystyle x=3\cos \varphi +\cos 3\varphi ,\;y=3\sin \varphi +\sin 3\varphi }$:

First the normal vectors are calculated from the parametric representation . The equation of the tangent is then: ${\displaystyle {\vec {n}}=({\dot {y}},-{\dot {x}})^{T}}$
${\displaystyle {\dot {y}}(\varphi )\cdot (x-x(\varphi ))-{\dot {x}}(\varphi )\cdot (y-y(\varphi ))=0}$

${\displaystyle (\cos 2\varphi \cdot x\ +\ \sin 2\varphi \cdot y)\cos \varphi =4\cos ^{2}\varphi \ .}$

For the nephroids have their points where they have no tangents. For can be divided by and finally gets ${\displaystyle \varphi ={\tfrac {\pi }{2}},{\tfrac {3\pi }{2}}}$ ${\displaystyle \varphi \neq {\tfrac {\pi }{2}},{\tfrac {3\pi }{2}}}$ ${\displaystyle \cos \varphi }$

• ${\displaystyle \cos 2\varphi \cdot x+\sin 2\varphi \cdot y=4\cos \varphi \ .}$

Equation of the secant

to the circle with center and radius : For the equation of the secant through the two points we get: ${\displaystyle (0,0)}$ ${\displaystyle 4}$ ${\displaystyle (4\cos \theta ,4\sin \theta ),\ (4\cos {\color {red}3}\theta ,4\sin {\color {red}3}\theta ))}$

${\displaystyle (\cos 2\theta \cdot x+\sin 2\theta \cdot y)\sin \theta =4\cos \theta \sin \theta \ .}$

For the secant degenerates into a point. For can be divided by and the equation for the secant results: ${\displaystyle \theta =0,\pi }$ ${\displaystyle \theta \neq 0\pi }$ ${\displaystyle \sin \theta }$

• ${\displaystyle \cos 2\theta \cdot x+\sin 2\theta \cdot y=4\cos \theta \ .}$

The two angles have different meanings ( is half the roll angle, is the parameter of the circle whose secants are calculated), but the result is the same straight line. So every above secant to the circle is also a tangent to the nephroids and ${\displaystyle \varphi ,\theta }$ ${\displaystyle \varphi }$ ${\displaystyle \theta }$ ${\displaystyle \varphi =\theta }$

• the nephroid is the envelope of the circular tendons.

Nephroids as the caustic of a circle: principle

Nephroids as caustic of a semicircle

Nephroids as caustic of a semicircle

The previous considerations also provide evidence that a nephroid appears as the caustic of a semicircle:

• If parallel rays of light in the plane fall into a reflective semicircle as shown in the figure, the reflected rays of light are the tangents of a nephroid. (see section: Nephroids in Daily Life)

proof

The circle has (as in the previous section) the zero point as its center and its radius . The circle then has the parametric representation ${\displaystyle 4}$

${\displaystyle k(\varphi )=4(\cos \varphi ,\sin \varphi )\ .}$

The tangent in the circle point has the normal vector . The reflected beam must then have the normal vector (according to the illustration) and go through the point of the circle . The reflected ray lies on the straight line with the equation ${\displaystyle K=k(\varphi )}$ ${\displaystyle {\vec {n}}_{t}=(\cos \varphi ,\sin \varphi )^{T}}$ ${\displaystyle {\vec {n}}_{r}=(\cos {\color {red}2}\varphi ,\sin {\color {red}2}\varphi )^{T}}$ ${\displaystyle K:4(\cos \varphi ,\sin \varphi )}$

${\displaystyle \cos {\color {red}2}\varphi \cdot x\ +\ \sin {\color {red}2}\varphi \cdot y=4\cos \varphi \ ,}$

which in turn is the tangent to the nephroids of the previous section at point

${\displaystyle P:(3\cos \varphi +\cos 3\varphi ,3\sin \varphi +\sin 3\varphi )}$

is (see above).

Evolute of a nephroid

Nephroids (red) and their evolutes (green),
magenta: a point P, its center of curvature M and the corresponding circle of curvature

The evolute of a plane curve is the geometric location of all centers of curvature of this curve. For a parameterized curve with a radius of curvature , the Evolute has the parametric representation ${\displaystyle {\vec {x}}(s)={\vec {c}}(s)}$ ${\displaystyle \rho (s)}$

${\displaystyle {\vec {X}}(s)={\vec {c}}(s)+\rho (s){\vec {n}}(s).}$

where is the appropriately oriented unit normal. ( points towards the center of curvature.) ${\displaystyle {\vec {n}}(s)}$ ${\displaystyle {\vec {n}}(s)}$

For a nephroid in the picture:

• The evolution of a nephroid is again a nephroid, half the size.

proof

The nephroids in the picture (the tips are on the y-axis!) Has the parametric representation

${\displaystyle x=3\cos \varphi +\cos 3\varphi ,\quad y=3\sin \varphi +\sin 3\varphi \ ,}$

is the unit normal

${\displaystyle {\vec {n}}(\varphi )=(-\cos 2\varphi ,-\sin 2\varphi )^{T}}$ (see above)

and has the radius of curvature (see above)

${\displaystyle \rho (\varphi )=3\cos \varphi }$.

So the Evolute has the parametric representation

${\displaystyle x=3\cos \varphi +\cos 3\varphi -3\cos \varphi \cdot \cos 2\varphi =\cdots =3\cos \varphi -2\cos ^{3}\varphi ,}$

${\displaystyle y=3\sin \varphi +\sin 3\varphi -3\cos \varphi \cdot \sin 2\varphi \ =\cdots =2\sin ^{3}\varphi \ ,}$

These equations describe a nephroid that is half the size and rotated 90 degrees (see picture and the section Equations of a Nephroid ).

Inversion (green) of a nephroid (red) on the blue circle

Inversion (mirroring of a circle) of a nephroid

The reflection

${\displaystyle x\mapsto {\frac {4a^{2}x}{x^{2}+y^{2}}},\quad y\mapsto {\frac {4a^{2}y}{x^{2}+y^{2}}}}$

on the circle with the center and radius forms the nephroid with the equation ${\displaystyle (0,0)}$ ${\displaystyle 2a}$

${\displaystyle (x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}}$

on the 6th degree curve with the equation

${\displaystyle (4a^{2}-(x^{2}+y^{2}))^{3}=27a^{2}(x^{2}+y^{2})y^{2}}$

from (see picture).

Nephroids in Daily Life

If light from an infinitely distant light source falls laterally on a concave , circular reflective surface, the envelope of the light rays forms part of a nephroid. Sometimes it is therefore also called "coffee cup caustic" ( caustic = focal line). You can also observe them on the street when the bare rims of a bicycle reflect the light on the ground: Since the sunlight hits the cylinder jacket of the bicycle rim in parallel , a focal surface is formed , the profile of which has the shape of half a nephroid and which, if you are lies slightly in the curve, forms part of a nephroid as a sectional figure with the level surface.

See also

• Cardioids

literature

1. ^ Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1. Springer-Verlag, 1995, ISBN 3-540-59188-5 , pp. 194, 200.

• D. Arganbright: Practical Handbook of Spreadsheet Curves and Geometric Constructions. CRC Press, 1993, ISBN 0-8493-8938-0 , p. 54.
• F. Borceux: A Differential Approach to Geometry: Geometric Trilogy III. Springer, 2014, ISBN 978-3-319-01735-8 , p. 148.
• EH Lockwood: A Book of Curves. Cambridge University Press, 1978, ISBN 0-521-05585-7 , p. 7.

Web links

Commons : Nephroid  - collection of pictures, videos and audio files

• Mathworld nephroid
• mathcurve: nephroid
• Xahlee: nephroid