Cycloid

A fixed point on a rolling circle draws a cycloid

A cycloid (from Latin cyclus or ancient Greek κύκλος kýklos = circle and ειδής -eidés = similar), also cyclic curve , wheel (running) or rolling curve , is the path that a point on the circumference of a circle describes when this circle rolls on a guide curve, for example a straight line. A trochoid is created if the leading curve is also a circle (locking circle), whereby the point under consideration lies outside or inside the rolling circle (passage circle). The use of cycloids and trochloids in drawing ornaments became widespread thanks to the toy Spirograph .

Mathematical representation of the cycloids

A cycloid can be represented as an analytical equation and in parametric representation. The parametric representation is

{\ displaystyle x = r (t- \ sin (t)); \ quad y = r (1- \ cos (t)),}

where denotes the radius of the circle and the parameter ("rolling angle"). The parameter can be eliminated from this . The analytical equation is ${\ displaystyle r}$ ${\ displaystyle t}$ ${\ displaystyle t}$

{\ displaystyle x (y) = r \ arccos \ left ({\ frac {ry} {r}} \ right) - {\ sqrt {y (2r-y)}},}

but only describes the part of the cycloid . ${\ displaystyle 0 \ leq x \ leq r \ pi}$

Any cycloids can be calculated using the following parameter representation :

{\ displaystyle x = rt-c \ sin (t); \ quad y = rc \ cos (t),}

where indicates the distance of the generating point from the center. Cycloids with are shortened, cycloids with are called lengthened. However, these arbitrary cycloids can no longer all be represented in an analytical form. ${\ displaystyle c}$ ${\ displaystyle c <r}$ ${\ displaystyle c> r}$

Properties of the cycloid

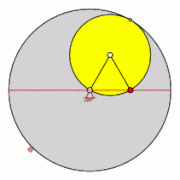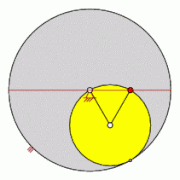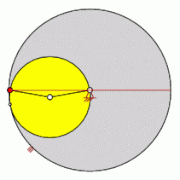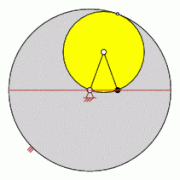
An ordinary cycloid is created when a circle rolls on a straight line. To put it graphically, a point on a tire of a moving bicycle (approximately the valve ) moves on an ordinary cycloid. The catacoustic , the evolute and the involute of the cycloid are themselves again cycloids. The centers of the circles of curvature of a cycloid lie completely on its evolute.

A shortened cycloid arises when the path of a point inside the circle is observed, for example the side radiators on a bicycle. An elongated cycloid, on the other hand, requires that a point outside of the rolling circle moves with the circle. These two curves are also called trochoid (from ancient Greek τροχός trochos "wheel").

Examples

Ordinary cycloids are described by points on the tread of a car tire or other running wheels (train, cable car) and by the points of marbles rolling along the tread .
Shortened cycloids are described by points with a radius smaller than that of the running surface, such as points on bicycle spokes or the attachment points of connecting rods on a steam locomotive .
Elongated cycloids are described by points with a radius greater than that of the tread; in the case of railroads , these would be all points on the flange .

The shape of an ordinary cycloid resembles a series of further arches , the elongated cycloid still has loops at the tips between the arches, while the tips of the shortened cycloids are rounded.

A brachistochrone or tautochrone is created by mirroring a cycloid on the x-axis .

The tautochrony of the cycloid

Tautochrony of the cycloid

Assuming that air resistance and friction are negligible, a freely movable mass point always reaches the lowest point in the same time from every starting point on an upturned cycloid. This property is also called tautochrony (line of equal fall time; ancient Greek ταὐτό tauto the same, χρόνος chronos time).

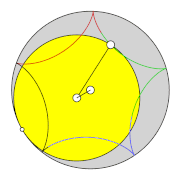
Epi-, peri- and hypocycloids

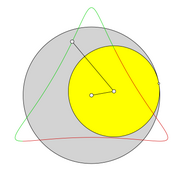
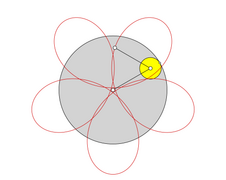
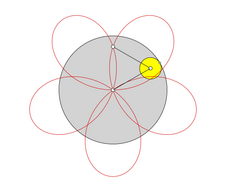
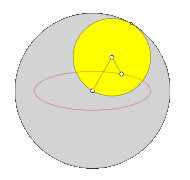
If the circle rolls outside on another circle, epicycloids are created ( ancient Greek ἐπίκυκλος epíkyklos , »secondary circle«). Their radius is equal to the sum of the radius of the guide circle and the diameter of the moving circle. Historically, attempts have been made to explain the observed planetary orbits with sometimes peculiar loops through the epicyclic theory . If a circle rolls around a fixed smaller circle, pericycloids are formed. In terms of transmission technology, the generating transmission of a pericycloid can be realized by rolling a ring gear around a stationary smaller wheel.

Two hypotrochoid

Double generation of epicycloids
Epicycloid i = 3/1
Pericycloid i = 3/4

Two hypotrochoid (animation)

In mathematics, both curves are often referred to as epicycloids, since the resulting curve can be generated either by rolling a circle on another circle or by rolling a circle around a circle. This realization is called the double generation of cycloids.

Ellipse as a special hypotrochoid at i = 2 (animation)

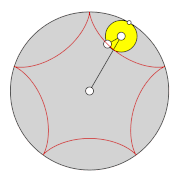
On the other hand, if the circle rolls inside the other circle, hypocycloids are formed. Each hypocycloid can also be generated analogously to epicycloids due to the double generation of a second pair of wheels. In the case of hypocycloids, the second generating pair of gears is also a hypocycloid: in one of the two pairs of gears, the diameter of the rotating inner gear is less than or equal, in the other one greater than or equal to the radius of the fixed ring gear.

Double generation of hypotrochoid with i = 3/1 or i = 3/2

Both epicycloids and hypocycloids are closed curves if and only if the (translation) ratio i of the radii r _R / r _{G is} rational and can be written as a shortened fraction of two whole numbers i _Z / i _N by abbreviation . In mathematical terms, this means: and . In this fraction, r _R is the radius of the ratchet track , i.e. the ratcheting and thus stationary wheel, and r _G is the radius of the gang pole track , namely the walking, i.e. the rotating wheel. In the technical implementation in the form of gears, the number of teeth is decisive, so that closed curves always result. ${\ displaystyle i_ {Z} = r_ {R} / \ operatorname {ggT} (r_ {G}, r_ {R})}$ ${\ displaystyle i_ {N} = r_ {G} / \ mathrm {ggT} (r_ {G}, r_ {R})}$

The number of peaks during one period is identical to the number i _Z .

Special hypo- and epicycloids
Hypocycloid i = 2/1 (Cardan circles)
Hypocycloid i = 3/1 (deltoids)
Hypocycloid i = 4/1 (astroids)
Epicycloid i = 1/1 (heart curve)

Special hypocycloids:

For i = 2 ( Cardanic circles ) the result is a straight hypocycloid, all points of which lie on one diameter.
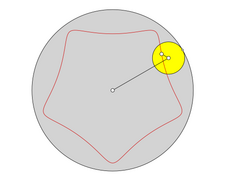
For i = 3 there is a deltoid (hypocycloid with 3 points)
For i = 4 there is an astroid : the diamond , as we know it from playing cards.

Special epicycloids:

For i = 1 the cardiac curve results ( cardioids )

The number of rotations of the moving wheel during one period is i _N . In the pictures, a different color is used for each part of the cycloid that forms during one revolution of the moving wheel.

Number of revolutions and number of intersections for cycloids
Hypocycloid i = 5/1
Hypocycloid i = 5/3
Hypocycloid i = 5/2
Hypocycloid i = 5/4

The number of intersection points s ₀ of epicycoids is the same . ${\ displaystyle i_ {Z} \ cdot (i_ {N} -1)}$

This equation also applies hypocycloids mi t , so if the diameter of the circumferential circle is less than or equal to the radius of the fixed circle. ${\ displaystyle i \ geqq 2}$

For pericycloids and for hypocycloids with applies . ${\ displaystyle i \ leqq 2}$ ${\ displaystyle s_ {0} = i_ {Z} \ cdot (i_ {Z} -i_ {N} -1)}$

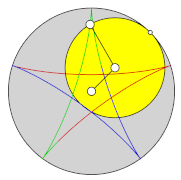
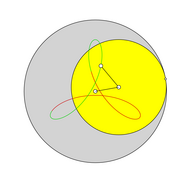
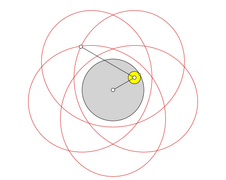
In addition to the usual, namely the pointed cycloids, there are the elongated and thus intertwined as well as the shortened and thus elongated epi, peri and hypercycloids, which are often also called epi, peri and hypotrochoids .

elongated, pointed, and intertwined hypotrochoid
elongated hypotrochoid i = 3/1
pointed hypocycloid i = 3/1
intertwined hypotrochoid i = 3/1
intertwined hypotrochoid i = 3/2
pointed hypocycloid i = 3/2
elongated hypotrochoid i = 3/2

Elongated epi-, peri- and hypotrochoid

All stretched epi-, peri- and hypotrochoids have the same number of intersection points as the pointed ones, i.e. s ₀ .

The elongated trochoid can be divided into trochoid with turning points and without.

The center of curvature of trochoid with turning points changes at each turning point from one side of the curve to the other. Thus, these trochoid have left and right turns. The number of left and right turns is i _Z and thus equal to the number of peaks. The number of turning points is thus . Points that produce stretched trochoid with turning points are near the edge of the rotating wheel.

{\ displaystyle 2 \ cdot i_ {Z}}

Points that produce stretched trochoid without turning points are further away from the edge of the rotating wheel.

Both areas are separated by the special case that the stretched trochoid runs through an approximate straight line. This is the case when the generating point is located on the ball's curve, and thus the following distance r _B having the center of the revolving wheel: . The number of approximated straight lines is equal to i _Z and thus equal to the number of peaks ${\ displaystyle r_ {B} = r_ {G} / (1 + i_ {Z} / i_ {N})}$

pointed and elongated hypotrochoid
pointed hypocycloids
elongated hypotrochoid with turning points
elongated hypotrochoid with approximated straight lines
elongated hypotrochoid without inflection points

Tangled epi-, peri- and hypotrochoid

The number of loops during a period is identical to the number i _Z and thus identical to the number of tips of the cycloid.

Tangled trochoid have at least i _Z more intersections than the (pointed) cycloid. The exact number of intersection points can only be determined with the help of transition curve points. A transition curve point creates a trochoid with points of contact. The number of transition curve points and thus of trochoidal points of contact is equal to the integer value of . Thus, when i _Z equals 1 , no points of contact occur . ${\ displaystyle (i_ {Z} / 2)}$

Unfortunately, transition curve points cannot be calculated analytically. The determination with the help of approximation methods is not complicated, but would go beyond the scope of this article. Therefore, only the phenomena for generating the variety of forms of the intertwined trochoid should be explained here. The shapes and their diversity are so fascinating that this fascination is used by a special toy, namely the spirograph . With a spirograph, various flowery-looking intertwined hypotrochoids can be created manually with the help of pencils. The pencils are put through holes in a cogwheel rotating in a ring gear and guided over a piece of paper until a closed curve results.

The fact that hypotrochoids appear again and again due to slight variation of the distance between the hole and the center of the rotating wheel can be explained using the special cases in which trochoid with points of contact arise.

entwined hypotrochoid with i = 5/1
pointed hypocycloids
Tangled hypotrochoid with 5 intersection points
Tangled hypotrochoid with 5 points of contact
Tangled hypotrochoid with 15 intersection points
Tangled hypotrochoid with 10-fold intersection point and 5 intersection points
Tangled hypotrochoid with 15 intersection points

Tangled trochoid with the minimum number of intersection points are created by points that are near the outer edge of the rotating wheel. The number of intersections is equal to the number of peaks plus i _Z .

The integer value of gives the number n _B of trochoid with points of contact . If n _{B is}
greater than zero, an intertwined trochoid with points of contact will be generated at some point when the generating point is shifted away from the circumference. The trochoid with contact points itself still has an unchanged number of self-intersection points. But if the generating point is moved further away, a trochoid is created without a point of contact, the number of intersections of which has increased by. If the underlying pair of wheels generates more than one trochoid with contact points, the same thing is repeated (several times) if the generating point is further removed from the circumference and thus reaches a point again in which a trochoid with contact points is generated. ${\ displaystyle (i_ {Z} / 2)}$ ${\ displaystyle (i_ {Z} / 2)}$ ${\ displaystyle 2 \ cdot i_ {Z}}$ ${\ displaystyle 2 \ cdot i_ {Z}}$
- All points that create trochoidal points of contact are between the outer edge of the rotating wheel and a concentric circle through the center of the stationary wheel. If the generating point is moved further away from the edge of the rotating wheel over the center of the stationary wheel, nothing changes in the number of intersection points and no further special cases occur.

Points which are further away from the center of the rotating wheel than the distance between the center points of the two trochoid generating wheels with the maximum number of intersection points n _Smax .

If i _{Z is} an even number, it is the maximum number of intersection points ${\ displaystyle n_ {Smax} = n_ {S0} +2 \ cdot n_ {B} \ cdot i_ {Z}}$
In all other cases, namely if i _{Z is} an odd number, the following applies: ${\ displaystyle n_ {Smax} = n_ {S0} + (1 + 2 \ cdot n_ {B}) \ cdot i_ {Z}}$

A trochoid that runs through the center of the stationary wheel and has more than one point of intersection is always a special case:

If i _{Z is} an even number , then this intertwined trochoid has at least one point of contact. If there are several points of contact, the points of contact and self-intersection are on top of each other
If i _{Z is} an odd number , then several points of intersection of the intertwined trochoid lie on top of one another.

Special trochoid

A very special special case are (pointed) hypocycloids with i = 2 , in which the diameter of the rotating wheel is equal to the radius of the stationary wheel. This cycloid is a straight line that is traversed twice and simultaneously has two points and points of contact. All non-sharpened trochoid are ellipses and the second generating gear is a hypotrochoid with the same gear ratio.

Hypotrochoid i = 2/1
Hypotrochoid: ellipse
Hypotrochoid: straight
Hypotrochoid: ellipse

For i = 2 of an epitrochoid, the envelope curve in the housing of the Wankel engine results from a special point inside the rolling circle .

Cycloidal teeth in gear technology

In the transmission technology which is cycloidal one of several techniques for teeth of gears and toothed racks . In cycloid gears , the contour of the cam discs follows a cycloid equidistantly .

Most important findings since the 16th century

The 17th century, known as the “Golden Age of Analysis”, was also relevant to the study of cycloids. The best mathematicians and natural scientists dealt with this particularly aesthetic curve.

The first publication on cycloids was made in 1570 by Gerolamo Cardano , who among other things describes the cardanic circles . Galileo Galilei undertook further geometric studies of cycloids in 1598. The first calculation of area and length on a cycloid succeeded in 1629 by the Italian Bonaventura Cavalieri . The Frenchman Marin Mersenne provided further research impulses in the same year .

In 1634 Gilles Personne de Roberval and in 1635 René Descartes and Pierre de Fermat made further progress through squaring . Roberval succeeded in constructing tangents in 1638, and Evangelista Torricelli in 1641 . Torricelli developed a quadrature in relation to the helix by 1643. The Englishman Christopher Wren showed in 1658 that the length of a cycloid is four times the diameter of the generating circle.

In response to a Newton competition from 1658, Blaise Pascal managed the rectification , the quadrature, the determination of the center of gravity and the cubatures. A quadrature over an infinite series was done in 1664 by Isaac Newton . Gottfried Wilhelm Leibniz developed the quadrature via the quadratrix in 1673 . The Dutchman Christiaan Huygens accomplished the evolution determination and tautochrony in 1673 .

Leibniz completed the integral representation in 1686. The last important finding was the brachistochron property by Johann I Bernoulli in 1697 .

literature

Joachim Erven, Dietrich Schwägerl: Mathematics for engineers . Walter De Gruyter, 4th edition, 2011, ISBN 978-3-486-70796-0 , pp. 211-215

Volker Jäkel: Division of a level moving plane into fields with qualitatively equal crosspoint paths with special consideration of the transition curve , VDI Verlag GmbH, Düsseldorf 2000, ISBN 3-18-332401-6 , chapter 4

Web links