radius
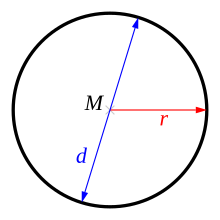
As a radius (from latin radius , literally "rod", "spoke" or "jet"), or semi-diameter is in the geometry of the distance between the center M of a circle designated and the cycle line. More generally, the distance between the center point and the spherical surface or sphere is also called this for a three-dimensional sphere or a - dimensional sphere . Occasionally, a line that connects the center of the figure to its edge is also called a radius or radius. The radius in the sense of a length is then given by the length of such a radius in the sense of a distance.
In astronomy , the radius is a measured quantity .
In general, every geometric object with a circular cross-section or a circular base area has a radius, including a cylinder or a cone .
geometry
The radius r corresponds to half the diameter d .
- .
The radius is related to the circumference U as follows:
- .
The radius is related to the circular area A as follows:
- .
astronomy
In astronomy, the radius of an approximately spherical object or an object (simplified or because of insufficient observation data ) acceptable as a spherical object is a characteristic number for a typical distance value from its center to its boundary surface (for example the geometric radius of a perfect sphere of equal volume). The interface is only clearly defined by the nature of the object in the case of a few types of astronomical objects (for example, dry rock planets with no atmosphere ). For most objects (e.g. stars ), the boundary surface on which the radius specification is based must be defined using other physical parameters ( e.g. opacity , i.e. the actually opaque part of a gaseous celestial body), and different radii can therefore be specified for an object depending on the boundary surface definition become.
Similarly, a radius can be specified for disk-shaped objects with a defined circumferential line, for example for galaxies or planetary ring systems .
The radius is a measured value if the distance to the object is known and its apparent size can be measured with sufficient accuracy. This is the case, for example, for the larger objects of the solar system and for numerous galaxies. Otherwise, a radius can be derived for many objects from other measured values (e.g. for stars from distance, brightness and spectral composition of the light , or for exoplanets, among other things, from the attenuation of the central star light during a transit ).