Earth flattening

The shape of the earth, which is slightly flattened compared to a sphere, can be approximated by an ellipsoid of revolution (for clarification, exaggerated representation that does not correspond to the dimensions of the semi-axes a and b according to WGS 84 entered here )

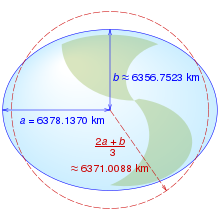
The earth flattening describes the geometrical flattening of the planet earth and thus its deviation from the spherical shape . It arises from the centrifugal force of the earth's rotation , which is greatest at the equator and zero at the poles . As a result, the sea ​​level approximates the shape of an ellipsoid of revolution whose semiaxes (radii) differ by 21.38 km ( = 6378.137 km at the equator or = 6356.752 km at the poles). The flattening of the earth is thus ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle f={\tfrac {a-b}{a}}=1:298{,}256\pm 0{,}001}$

This corresponds to about 0.3% of the earth's radius and would cause noticeable errors in calculations on a spherical surface.

The earth would be just as flattened if it had no oceans . Because the material of the earth's interior is somewhat plastic , so that the earth (like other planets in the solar system ) had to give in to this force over time.

Gravity flattening

→ Main article : Flattening of gravity

This deformation of the earth by the factor f also causes differences in the gravitational field , the gravity flattening :

${\displaystyle \beta ={\frac {g_{\mathrm {P} }-g_{\mathrm {A} }}{g_{\mathrm {A} }}}}$

With

• the acceleration due to gravity at the poles ${\displaystyle g_{\mathrm {P} }}$
• the acceleration due to gravity at the equator. ${\displaystyle g_{\mathrm {A} }}$

For the most internationally used earth model GRS80 is and . This results in the flattening of gravity as β = 0.0053025 = 1: 188.6 , i.e. H. the force of gravity is at the poles by about 0.53 percent higher than at the equator. Due to the difference in gravity, a person weighing 80 kg has a weight of 787 N (about 80.2 kg) at the earth's poles, but only one of 782 N (about 79.7 kg) at the equator. ${\displaystyle g_{\mathrm {P} }=9{,}83218\,\mathrm {m} /\mathrm {s} ^{2}}$ ${\displaystyle g_{A}=9{,}78032\,\mathrm {m} /\mathrm {s} ^{2}}$

Earth's mantle, core and their effect

The flattening of gravity also depends on the structure of the earth's interior. The theory of the equilibrium figures says that a homogeneous body of the shape of the earth , its mean density (5.521 g / cm³) and its rotation time (23 hours 56 minutes) must have a geometric flattening f '= 1: 230 ( Maclaurin- Ellipsoid ).

In fact, at 1: 298, the earth is much more spherical because its core is more than twice as dense as the mantle. This means that the centrifugal force is less important.

The greater density of the earth's core can be taken into account with a two-shell model of the earth's interior. This model by Emil Wiechert also explains the observed gravity field in near space better - and, despite its simplicity, agrees surprisingly well with the results of seismology . Finer geophysical models of the earth subdivide the crust, mantle, and core of the earth twice , which, however, already reaches the limits of predictability. Mass , pressure , density and gravity have to fit together in every single layer and overall, as well as the course of temperature and the modulus of elasticity in the depth.

More precise information

The figure of the earth and the earth's gravity field can be calculated to a few centimeters or 0.0001 percent. One knows z. For example, since the fourth artificial earth satellite , Vanguard 1  (1958), that the flattening is stronger in the southern hemisphere than in the north (the catchphrase at the time spoke of a “pear shape”): the ellipsoid half-axis  b is 16 meters shorter in the south and in North longer than mean . This causes a periodic path disturbance, as with changing pressure on a top .

Further analyzes ( terrestrial and with geodetic satellites ) meanwhile allow the shape of the sea ​​level (the geoid ) to be precisely described with millions of coefficients - a prerequisite for the now everyday GPS and also for modern, precise space travel .

See also

• dynamic flattening
• Reference ellipsoid
• Degree measurement , plumb direction
• Land surveying , network expansion
• Clairaut's Theorem (Earth Measurement)
• Measurements from 1736 by Charles Marie de La Condamine

Individual evidence

1. ^ Richard H. Rapp: Current estimates of mean Earth ellipsoid parameters. In: Geophysical Research Letters. 1, 1974, pp. 35-38, doi: 10.1029 / GL001i001p00035