Spinning top
A top is a ( rigid ) body that rotates around an axis. Otherwise it can move freely ( free top ), but can also be forced in a certain direction with an axis ( tied top ). In physics, gyroscopes do not necessarily have to be rotationally symmetrical .
Demarcation
As gyroscope or gyro (Greek.) Are also called measuring instruments that perform tasks similar to those of a gyroscope , even if they do not contain a rotating top. Examples are laser gyroscopes , fiber optic gyroscopes or vibration gyroscopes .
use
- Children's toys
Spinning tops also serve as children's toys , which are rotated around a vertical axis on a base and then roughly maintain the axial direction for a while, with the top moving around on the base ( examples of toy tops ).
The spinning top is one of the oldest toys that can be found at archaeological sites. In addition to being a toy, spinning tops have also historically been used for games of chance and fortune- telling . - Technology
( examples of technical applications )- Axis stability
In technology, gyroscopes are used, for example, for stabilization and navigation, since the direction of the angular momentum remains the same if no torque is acting on it. The reason for this is the conservation of angular momentum . If the axis of rotation agrees with the direction of the angular momentum, it does not change either. - as energy storage.
- Axis stability
physics
General
A top rotating around its figure axis maintains its orientation in space with cardanic suspension , even if the support frame is rotated. The weak torque that acts through the bearing friction of the suspension produces a negligibly small change in the angular momentum that does not lead to an observable change in the axis of rotation . Compared to the stationary top, large external moments are required to change the orientation.
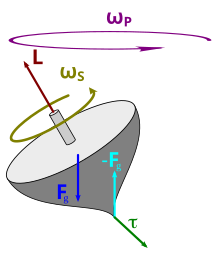
It can also be observed: If an attempt is made to tilt its axis of rotation on a rotating top, then a force can be registered perpendicular to the direction of tilt of the axis of rotation. The faster the top rotates, the greater the forces (which are also called gyroscopic forces ). This can be explained by the high angular momentum of the top, which has to be changed in its direction. Its change takes place in the direction in which the axis of rotation is tilted and requires a torque that lies in the tilting plane. The torque to be applied determines the force effect perpendicular to the direction of tilt.
Conversely, a torque perpendicular to a rotating gyroscope does not cause it to change its orientation around the axis of the torque, but rather tilts it in the direction of the torque axis.
The explanation of the gyroscopic behavior may be computationally logical, but the angular momentum itself is not a very clear variable. Therefore, to check the plausibility of the processes, assume a body that is enclosed in the top. As long as the top rotates stably around its figure axis, the top only has to exert a centripetal force on the enclosed body . It gets exciting when the rotation axis of the top is tilted and the movement of the body is analyzed. Then the enclosed body also moves in the tilting direction, but constantly changes its side and thus its direction of movement, i.e. its speed . The enclosed body executes a sinusoidal oscillation in the direction of the vertical to the tilting plane . This means that there is a rest point at the apex and in the "zero crossing", when changing the tilting side, the greatest change in the "tilting speed" and thus the greatest force takes place. So the top wants to break out of the way when tilting.
Gyroscopic moment
If the angular speed of the gyro ω is significantly greater than the tilting angular speed Ω , then the following approximate calculation applies. The change in angular momentum results from the change in angle d φ and the alignment of the tilt axis according to the following formula. The cross product means that only the component of angular momentum that is perpendicular to the tilting axis is of interest here . The portion parallel to the tilt axis is neglected.
The change in angle d φ over time d t also represents the tilt angle velocity Ω . In the next step, the change in angular momentum is inserted into Euler's law of angular momentum. The resulting torque M follows from the gyroscopic parameters rotation rate ω and moment of inertia of the figure axis I , combined with the tilt angle speed Ω .
Moment of deviation
The moment of deviation is a measure of the tendency of a gyroscope to change its axis of rotation if it is not rotating around one of its main axes of inertia.
Euler's gyroscopic equations
A generalization of the gyroscopic motion results from the angular momentum law. The angular momentum follows from the product of the inertia tensor and the rotational speed of the top. Just as the mass for the translational movement indicates how “difficult” a body is to accelerate, the inertia tensor for the rotational movement describes how “difficult” it is to change the rotation of a top. The moments of inertia for rotations around the various axes of rotation of the gyro are summarized in the inertia tensor . If the change in angular momentum is calculated by deriving it with respect to time, we get:
This means that the change in the angular momentum requires a torque . It depends on the change in the spatial direction of the angular momentum (term ) and on the change in the instantaneous angular velocity (term ).
By rotating in a reference system in which the inertia tensor forms a diagonal matrix , the individual components of the vectors can be reformulated into a particularly simple system of differential equations. They are known as Euler's gyro equations after their discoverer Leonhard Euler .
Classification
According to properties:
- In a symmetrical top , at least two main moments of inertia are equal. This group includes the rotationally symmetrical toy tops or blocks with two sides of equal length. One of its main axes coincides with the figure axis. Perpendicular to it, through its center of gravity, it has an infinite number of equal main equatorial axes. The ellipsoid of inertia of a symmetrical top is always rotationally symmetrical.
- With a flattened top or oblate top (e.g. disk), the figure axis has a greater moment of inertia than the equatorial axes. ( I 1 = I 2 < I 3 )
- In contrast, the elongated top or prolate top (e.g. rod) has a smaller moment of inertia in the direction of the figure axis than in the other axes. ( I 1 = I 2 > I 3 )
- In a spherical top , all three main moments of inertia are the same. Examples are cubes and balls . A sphere also has an infinite number of identical main axes. ( I 1 = I 2 = I 3 )
- If there are three different main moments of inertia, one speaks of an asymmetrical top .
After hanging:
- A gyroscope is force-free when it is not acted on by external torques ; that is, all external forces outside the center of gravity must cancel each other out. For this purpose, the point of support of the gyro must be, for example, just below the center of gravity of the gyro, as a cardanic suspension (center of gravity in the center of the gimbal frame), or as a Kleinscher gyro (support directly in the center of gravity of a gyro body hollowed out below). The equations of motion for a force-free symmetrical top are easier to solve than for a heavy top. Its movement generally consists of actual rotation and nutation . In nutation, the angular momentum and the momentary axis of rotation have different directions. This occurs when the moment of inertia is direction-dependent (the moments of inertia are not all the same) and the rotation does not take place around the axis of a main moment of inertia. If the top is not symmetrical, it can lead to more complicated movements.
- The opposite is the heavy top: if a toy top is tilted, for example, gravity tries to tip it over. Since the resulting torque is perpendicular to the angular momentum, the angular momentum only changes its direction. The top rotates around an axis that goes straight up through its support point. This rotation is called precession . The equations of motion can only be solved approximately here (especially for fast gyroscopes).
- A tethered top is limited in its degrees of freedom and exerts gyroscopic moments on its suspension when it rotates.
Examples of toy spinning tops

The toy is available in numerous designs and variants:
- Humming top
- Spinning top or Preckel
- Drawing top
- Whip top
- Whistling top
- Dueling top
- Beyblade
- Beigoma
- Dreidel
- Take
- Sakai top
- Standing top (revolving top), it turns upside down when turning. Helene Sperl applied for a patent on October 7, 1891.
- the gyrotwister
- The Celtic rocking stone is a "top" with a special shape and mass distribution. As a result, the roughly elliptical body rotates normally in one direction, but reverses rotation in the other direction.
- Fidget spinner
Technical applications
- Gyroscope (measurement of the axis) and gyrometer (measurement of the rotational speed)
- Gyroscope as energy storage (see also rotating mass storage ).
- Inertia wheels for the attitude control of missiles
- The Levitron is a spinning magnet that hovers in the air above an oppositely polarized, ring-shaped magnetic field. Its gyratory motion prevents it from tipping over and being attracted to the magnetic ring. - Video ( Ogg ; 1.13 Mbps)
- The gyro compass aligns itself - through the rotation of the earth - towards the North Pole.
At the beginning of the 20th century spinning tops - e.g. B. the Musil color spinning top - used to investigate human color perception.
Popular culture of the top
In the 2010 film Inception , the protagonist Cobb uses a top as a " totem ".
literature
- Richard Grammel Der Kreisel: Its Theory and Its Applications , 2 volumes, 2nd edition, Springer Verlag, 1950 (first Vieweg 1920).
- Felix Klein , Arnold Sommerfeld : About the theory of the top . Teubner, Stuttgart 1965.
- Heinz Parkus : Mechanics of Solid Bodies . 2nd Edition. Springer textbook, Vienna / Berlin 1966.
- H. Westphal: Physics. A textbook . 24th edition. Springer-Verlag Berlin / Heidelberg 1963, chap. I and III.
- Renée Holler: Roundabout. Hugendubel, Munich 1989, ISBN 3-88034-401-9 .
Web links
- Script on experimental physics (PDF; 421 kB), including a relatively detailed consideration of rotary movements
- By centrifugal mechanically stabilized two-wheeled transport (English)
- World record top with 60 kg
- International Top Spinners Association