angular momentum

Physical size
Surname	angular momentum
size type	effect
symbol	${\displaystyle {\vec {L}},{\vec {J}}}$
Size and unit system unit dimension S.I N m s = kg m 2 s −1 _ _ _ _ M · L2 · T − 1

Play media file

Angular momentum conservation demonstration experiment (video, 18 s). As the person applies a torque, the angular momentum of the wheel changes direction to the vertical (red arrow). According to the principle of action equals reaction, the swivel chair receives an opposite angular momentum (yellow arrow) from the reaction moment. The vertical angular momentum of zero is preserved.

The angular momentum (in mechanics also twist or obsolete momentum or momentum , in quantum mechanics in some cases also spin ) is a physical conserved quantity . For example, a system has angular momentum when it rotates about its center of mass , such as a top , an athlete performing a pirouette , or a planetary system .

The angular momentum is a vector quantity, namely – like the torque and the angular velocity – a pseudo -vector . Its dimension is the product of mass, length and speed. In the SI system of units , it is measured in newton meter seconds ( ). Its symbol is or . ${\displaystyle \mathrm {N\,m\,s} }$ ${\displaystyle {\vec {L}}}$ ${\displaystyle {\vec {J}}}$

The angular momentum of a system is the sum of the angular momenta of its components. The angular momentum of a component of the system is generally made up of two components (see #The angular momentum of a rigid body ):

1. the orbital angular momentum, as the proportion that arises due to the movement of a mass-bearing body with respect to a reference point, provided that the body does not move directly towards or away from the reference point.
2. the intrinsic angular momentum, as the part that is not orbital angular momentum. In mechanics, this part is caused by the rotation around the center of mass of the body. In quantum mechanics, it is spin .

The angular momentum always refers to the point in space that is chosen as the reference point for the rotary movement. In a freely rotating system, the center of gravity is often set as the reference point, in astronomy mostly the center of gravity of the central star . When the rotation is dictated by a bearing , a point on the axis is usually chosen.

The angular momentum can generally be calculated as the vector product of the position vector and the momentum of the body: ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {p}}}$

${\displaystyle {\vec {L}}={\vec {r}}\times {\vec {p}},}$

or using the inertia tensor and the angular velocity to: ${\displaystyle \mathbf {\Theta } }$ ${\displaystyle \omega }$

${\displaystyle {\vec {L}}=\mathbf {\Theta } \cdot {\vec {\omega }}.}$

In quantum mechanics, angular momentum is described by the angular momentum operator. It turns out that it is a quantized quantity. The magnitude of the angular momentum is always an integer or half-integer multiple of the reduced Planck constant . The orientation of the angular momentum is also quantized. It is subject to directional quantization with respect to the quantization axis . The role of angular momentum is played by spin , which is not associated with spatial motion. Thus, the angular momentum operator consists of the components orbital angular momentum operator and spin operator . ${\displaystyle {\hat {\mathbf {L} }}={\hat {\mathbf {r} }}\times {\hat {\mathbf {p} }}}$

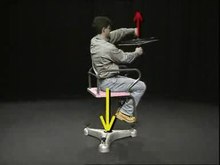
In 1775 Leonhard Euler introduced the principle of angular momentum as a fundamental principle in mechanics that was independent of Newton's laws . It states that a torque must act on the system in order to change the angular momentum. The conservation of angular momentum can be experienced in many places in everyday life (see video, or pirouette effect ).

Definition and Illustration

Using the right-hand rule , the direction of the angular momentum vector can be determined as the direction of the thumb.

For a point mass moving in place with momentum , the angular momentum is given by the cross product ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {p}}=m{\vec {v}}}$

${\displaystyle {\vec {L}}={\vec {r}}\times {\vec {p}}}$

Are defined. The point of reference is the origin . For the angular momentum about another reference point , one has to replace by . ${\displaystyle {\vec {r}}={\vec {0}}}$ ${\displaystyle {\vec {r}}_{0}}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {r}}'=({\vec {r}}-{\vec {r}}_{0})}$

The case in which the mass point performs a level circular movement around the origin is suitable for illustration. Then the angular momentum vector is perpendicular to the plane of the circle, i.e. in the direction of the axis of the circular motion, and has the amount

${\displaystyle L=mrv=mr^{2}\omega }$.

The angular momentum increases with it

• proportional to higher angular velocity , ${\displaystyle \omega }$
• also proportional to larger mass , ${\displaystyle m}$
• greater distance of this mass to the axis of rotation, however, in a quadratic ratio. ${\displaystyle r}$

The angular momentum vector points in the direction in which a right-hand screw would advance with the same direction of rotation. The corkscrew rule or right-hand-rule applies: if the curled fingers of the right hand indicate the direction of rotation, the thumb points in the direction of angular momentum (see picture). The fact that the right hand must be used for this rule and not the left is due to the definition of the cross product of two vectors.

The angular momentum of an extended body at a specific reference point is obtained by forming the angular momenta of its mass points at this reference point and adding them vectorially.

Even if the name suggests otherwise, such bodies also have an angular momentum that, seen graphically, do not rotate at all. Even a body moving in a straight line and not rotating about itself has angular momentum if the reference point is chosen so that it does not lie on the orbit of the body's center of mass . The angular momentum is then simply calculated from the product of mass, velocity and the vertical distance of the reference point from the orbit. It is therefore always possible to find reference systems in which no angular momentum is associated with the movement of the center of mass. The angular momentum of a body rotating around its center of mass, on the other hand, only vanishes in a co-rotating, i.e. accelerated reference system .

conservation of angular momentum

Experience has shown that the angular momentum of an isolated physical system remains unchanged in terms of amount and direction, regardless of the internal forces and interactions between the components of the system. This is called conservation of angular momentum . Almost perfectly isolated systems are e.g. B. the atomic nuclei , the molecules in rarefied gases and astronomical objects in the universe. Kepler 's second law , according to which a planet moves faster in its eccentric orbit the closer it is to the sun, can be derived from the conservation of angular momentum.

The conservation of angular momentum also applies in the presence of external forces if these forces do not exert a total torque on the system. In a homogeneous gravitational field, this applies e.g. B. for the angular momentum of each body about its own center of mass . If the external forces on different parts of a system are parallel to each other, then the component of the angular momentum parallel to the forces remains the same.

Conservation of angular momentum can be seen, for example, in toy spinning , discus throwing and the pirouette effect .

The conservation of angular momentum applies to any physical system (e.g. also electromagnetic fields) and can be derived using the Noether theorem from the fact that the physical laws do not depend on the orientation of the system under consideration in space.

Translation, rotation, mirroring

While position vector and momentum reverse their direction in a point reflection around the origin of coordinates, that of the angular momentum remains unchanged with respect to the center of the disk. (In the image, the vectors are in bold and not drawn with an arrow.) ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {p}}=m{\vec {v}}}$ ${\displaystyle {\vec {L}}=m{\vec {r}}\times {\vec {v}}}$

The magnitude and direction of the angular momentum of a point mass depend on which point is chosen as the reference point. Moving the reference point changes the vector of each location in and the angular momentum in ${\displaystyle {\vec {x}}^{\,\prime }={\vec {x}}+{\vec {a}}}$

${\displaystyle {\vec {L}}^{\prime }={\vec {L}}+{\vec {a}}\times {\vec {p}}.}$

The center of mass or a point that is at rest during the rotations under consideration, i.e. on the axis of rotation, is often chosen as the reference point .

The cross product of two vectors is always perpendicular to the plane spanned by them, but a rotation of the system under consideration rotates both the position vectors and the orbital velocities by the same amount, which means that the angular momentum is also rotated in the same way.

In the case of point reflection at the reference point, the location merges into the opposite location. The sign of the velocity with respect to this point is also reversed. When the cross product is formed, these two sign changes compensate each other, so that the angular momentum does not change in the case of point reflection. In this way it differs from the behavior of the velocity or the position vector: Angular momentum belongs to the class of pseudo -vectors .

Euler's law of angular momentum

→ Main article : Twist set

In order to change the momentum of a body, a force must act. More precisely, the change in momentum over time is the force:

${\displaystyle {\frac {\mathrm {d} {\vec {p}}}{\mathrm {d} t}}={\vec {F}}.}$

In 1754 Leonhard Euler formulated Euler 's angular momentum theorem in a completely analogous way, according to which the change in angular momentum with respect to the origin over time is equal to the applied torque around the origin: ${\displaystyle {\vec {M}}}$

${\displaystyle {\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {M}}.}$

In order to change the angular momentum of a body, a torque must occur. A torque is the cross product of distance vector and force : ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {F}}}$

${\displaystyle {\vec {M}}={\vec {r}}\times {\vec {F}}.}$

The law of angular momentum results when one derives the angular momentum with respect to time, for example for a point mass at the location : ${\displaystyle {\vec {x}}}$

${\displaystyle {\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\dot {\vec {L}}}={\frac {\mathrm {d} }{\mathrm {d} t}}[{\vec {x}}\times {\vec {p}}]={\underline {{\dot {\vec {x}}}\times {\vec {p}}}}+{\vec {x}}\times {\dot {\vec {p}}}={\vec {x}}\times {\vec {F}}={\vec {M}}.}$

Since the velocity and momentum are parallel, their cross product is omitted in the underlined term. In order to change the (orbital) angular momentum of a point mass , a moment is required that corresponds to the moment of the force acting on the point mass . In the case of an extended body, a force couple with a resultant force can also trigger a change in angular momentum, as far as the intrinsic angular momentum is concerned, see below. Of course, the intrinsic angular momentum does not apply to a point mass. ${\displaystyle {\vec {M}}}$ ${\displaystyle {\vec {F}}}$ ${\displaystyle {\vec {F}}={\vec {0}}}$

If the force is a central force , the angular momentum around the center is conserved because the change in angular momentum over time – the acting moment of the central force – disappears: ${\displaystyle {\vec {F}}=f{\tfrac {\vec {x}}{|{\vec {x}}|}}}$

${\displaystyle {\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {x}}\times \left(f{\frac {\vec {x}}{|{\vec {x}}|}}\right)={\frac {f}{|{\vec {x}}|}}\underbrace {{\vec {x}}\times {\vec {x}}} _{={\vec {0}}}={\vec {0}}.}$

Consequently, the angular momentum about the center is constant over time. This applies in particular to planetary movements around a central star.

Plane orbit, set of surfaces

If the angular momentum of a point mass (e.g., the Earth orbiting the sun) remains at its initial value at all times, then the trajectory of the point mass is in a plane.

Because the cross product is perpendicular to its factors and at all times applies to the angular momentum with respect to the coordinate origin ${\displaystyle t}$

${\displaystyle {\vec {x}}(t)\cdot {\vec {L}}(t)={\vec {x}}(t)\cdot {\bigl (}{\vec {x}}(t)\times m{\vec {v}}(t){\bigr )}=0,}$

if the mass and the orbital velocity of the point mass are If now the angular momentum is independent of time, then every orbital point satisfies the plane equation ${\displaystyle m}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle {\vec {L}}(t)={\vec {L}}(0),}$

${\displaystyle {\vec {x}}(t)\cdot {\vec {L}}(0)=0.}$

It is therefore a motion in the plane through the center of mass of the system perpendicular to the angular momentum.

Then Kepler's second law (also called the law of areas) applies: The trajectory to the planet sweeps out areas of equal size in the same amount of time.

Because in a short time the driving line changes and sweeps over the area of ​​the triangle with these two sides. The triangle is half the size of the parallelogram spanned by the two vectors, the content of which is given by the absolute value of the cross product. Consequently, the line of travel sweeps over the surface over time ${\displaystyle \mathrm {d} t}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {v}}\mathrm {d} t}$ ${\displaystyle \mathrm {d} t}$

${\displaystyle \mathrm {d} F={\frac {1}{2}}\left|{\vec {x}}(t)\times {\vec {v}}(t)\,\right|\,\mathrm {d} t={\frac {1}{2\,m}}{\bigl |}{\vec {L}}{\bigr |}\mathrm {d} t.}$

Consequently, if angular momentum does not change with time, surface velocity is constant. This fact can also be generalized to situations in which the angular momentum changes, see angular momentum #area theorem .

The area law also applies in relativistic physics if the energy is also conserved. Because in relativistic physics is ${\displaystyle E}$

${\displaystyle {\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}={\frac {\vec {p}}{E}}\,c^{2}}$

and

${\displaystyle \mathrm {d} F={\frac {c^{2}}{2\,E}}{\bigl |}{\vec {L}}{\bigr |}\mathrm {d} t.}$

For plane orbits, there is a relationship between angular momentum and angular velocity that is relevant to the Runge-Lenz vector : ${\displaystyle {\vec {L}}}$ ${\displaystyle {\vec {\omega }}}$

${\displaystyle {\vec {L}}=mr^{2}{\vec {\omega }}.}$

To prove this, the speed is broken down into a radial and an azimuthal component (see polar coordinates/speed ), . In the cross product with the radial velocity vanishes and one obtains ${\displaystyle {\dot {\vec {r}}}={\dot {r}}{\vec {e}}_{r}+r{\dot {\varphi }}{\vec {e}}_{\varphi }}$ ${\displaystyle {\vec {r}}=r{\vec {e}}_{r}}$

${\displaystyle {\vec {L}}={\vec {r}}\times m{\dot {\vec {r}}}=mr^{2}{\dot {\varphi }}\,{\vec {e}}_{r}\times {\vec {e}}_{\varphi }=mr^{2}{\dot {\varphi }}{\vec {e}}_{z}=mr^{2}{\vec {\omega }}.}$

The angular momentum of a rigid body

The angular momentum of a body is the sum of the angular momenta of its components:

${\displaystyle {\vec {L}}=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {x}}}_{n}}$

or for a body with continuous mass distribution the integral:

${\displaystyle {\vec {L}}=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times {{\vec {v}}({\vec {x}})}}$

• ${\displaystyle m_{1\ldots N}}$… the masses of the mass points of the body with discrete mass distribution
• ${\displaystyle \rho ({\vec {x}})}$… the mass density of the continuous mass distribution
• ${\displaystyle {\vec {x}}_{1\ldots N}}$and … the locations and velocities of the mass points of the body with discrete mass distribution ${\displaystyle {\dot {\vec {x}}}_{1\ldots N}}$
• ${\displaystyle {\vec {v}}({\vec {x}})}$… the velocity field, which indicates the velocity at which the mass is moving at that location ${\displaystyle {\vec {x}}}$

With the help of the center of mass of a body and its location coordinates as well as its center of mass velocity , related location coordinates and the angular velocities of the mass points can be defined. Then the speeds can be expressed as: ${\displaystyle {\vec {s}}}$ ${\displaystyle {\dot {\vec {s}}}}$ ${\displaystyle {\vec {\chi }}:={\vec {x}}-{\vec {s}}}$ ${\displaystyle {\vec {\omega }}_{n}}$

${\displaystyle {\begin{aligned}{\dot {\vec {x}}}_{n}&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}_{n}\\{{\vec {v}}({\vec {x}}})&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}.\end{aligned}}}$

In the case of a rigid body whose orientation to the reference point is constant, all angular velocities are also the same . The angular momentum is then: ${\displaystyle (\forall n:{\vec {\omega }}_{n}\equiv {\vec {\omega }})}$

${\displaystyle {\begin{aligned}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right){\text{ bzw.}}\\{\vec {L}}&=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\int \mathrm {d} ^{3}\chi \rho ({\vec {\chi }})\,{\vec {\chi }}\times \left({\vec {\omega }}\times {\vec {\chi }}\right){\text{ oder verallgemeinert}}\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\mathbf {\Theta } _{s}\cdot {\vec {\omega }}.\end{aligned}}}$

Here are additional

• ${\displaystyle M=\sum _{n}m_{n}}$the total mass of the body and
• ${\displaystyle \mathbf {\Theta } _{s}=\int \mathrm {d} ^{3}x\rho ({\vec {x}})\,[({\vec {x}}\cdot {\vec {x}})\,\mathbf {1} -{\vec {x}}\otimes {\vec {x}}]}$the inertial tensor of the body referred to its center of mass.

derivation

---

derivation

Various conversions, the Graßmann identity (BAC-CAB formula), and the definition of the center of mass are used in the derivation:

${\displaystyle {\begin{array}{lllll}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|+{\vec {0}}={\vec {s}}-{\vec {s}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}+{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\vec {x}}_{n}-{\vec {s}}={\vec {\chi }}_{n}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\text{Graßmann-Identität}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,\left({\vec {\omega }}\left({\vec {s}}\cdot {\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)\right)&\left|{\text{Summe in die Klammer}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+{\vec {\omega }}\left({\vec {s}}\cdot \sum _{n}m_{n}{\vec {\chi }}_{n}\right)-\sum _{n}m_{n}{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)&\left|\sum _{n}m_{n}\chi _{n}={\vec {0}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+0\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Graßmann-Identität}}\right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\omega }}\left({\vec {\chi }}_{n}{\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {\omega }}{\vec {\chi }}_{n}\right)&&\left|{\text{Dyadisches Produkt}}\otimes \right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left(({\vec {\chi }}_{n}{\vec {\chi }}_{n})\mathbf {1} -{\vec {\chi }}_{n}\otimes {\vec {\chi }}_{n}\right){\vec {\omega }}\end{array}}}$

The first term is called the orbital angular momentum , the second term is the intrinsic angular momentum. ${\displaystyle M{\vec {s}}\times {\dot {\vec {s}}}}$

The intrinsic angular momentum

→ Main article : Inertial tensor

The intrinsic angular momentum of a rigid body is the fraction of its angular momentum that can be represented by rotation about its center of mass . With the help of the angular velocity and the inertia tensor , each related to the center of mass , it can be calculated as their matrix product: ${\displaystyle {\vec {s}}}$ ${\displaystyle {\vec {\omega }}_{s}}$ ${\displaystyle \mathbf {\Theta } _{s}}$ ${\displaystyle {\vec {s}}}$

${\displaystyle {\vec {L}}_{s}=\mathbf {\Theta } _{s}\cdot {\vec {\omega }}_{s}.}$

Generally pointing and not in the same direction - a rotating body "wobbles" when it is free to move, or exhibits imbalance when the direction of the axis is fixed. Only when rotating around one of the main axes of inertia of the body are and parallel, so that the conservation of angular momentum also causes the axis of rotation to remain in the same direction and thus the moment of inertia to be constant. The inertia tensor is symmetric and therefore the principal axes of inertia are pairwise orthogonal. From the inertia tensor one can calculate the moment of inertia and the main axes of inertia for any axis of rotation by solving the eigenvalue problem . ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {L}}_{s}}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {L}}_{s}}$

Angular momentum in the theory of relativity

In the theory of relativity , angular momentum cannot be embedded in a four-vector. This is already evident from the fact that under Lorentz transformations such as transformed. This problem is circumvented by introducing the angular momentum tensor. This is defined as ${\displaystyle L_{i}=\varepsilon _{ijk}x_{j}p_{k}}$ ${\displaystyle L'_{i}=\varepsilon _{ijk}\Lambda ^{\mu j}x_{\mu }\Lambda ^{\nu k}p_{\nu }}$ ${\displaystyle M^{\mu \nu }}$

${\displaystyle M_{\mu \nu }=x_{\mu }p_{\nu }-p_{\mu }x_{\nu }}$

and its entries are

${\displaystyle \left(M_{\mu \nu }\right)={\begin{pmatrix}0&-N_{x}&-N_{y}&-N_{z}\\N_{x}&0&L_{z}&-L_{y}\\N_{y}&-L_{z}&0&L_{x}\\N_{z}&L_{y}&-L_{x}&0\end{pmatrix}}}$

With ${\displaystyle N_{i}=\gamma mcx_{i}-cp_{i}t.}$

See also

• Specific angular momentum
• Galilean transformation as the basis of classical mechanics

literature

• Dieter Meschede : Gerthsen physics . 24th revised edition. Springer, Heidelberg Dordrecht London New York 2010, ISBN 978-3-642-12893-6 , p. 32-33, 40, 81-98 , doi : 10.1007/978-3-642-12894-3 .
• Florian Scheck : Theoretical Physics 1 . 8th edition. Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-71377-7 , p. 13-18, 20, 184-185 .

web links

Commons : Angular Momentum  - Collection of images, videos and audio files

Wiktionary: Angular momentum  – explanations of meaning, word origin, synonyms, translations

• Video: Swivel Chair Experiments on Conservation of Angular Momentum . Institute for Scientific Film (IWF) 2003, made available by the Technical Information Library (TIB), doi : 10.3203/IWF/C-14826 .
• Video: On the Vector Nature of Angular Momentum . Institute for Scientific Film (IWF) 2003, made available by the Technical Information Library (TIB), doi : 10.3203/IWF/C-14827 .

Remarks

1. ↑ The formally identical unit joule second should not be used because the joule is reserved for energy, a scalar quantity.

itemizations

1. ↑ Clifford Truesdell : The Development of the Swirl Theorem . In: Society for Applied Mathematics and Mechanics (ed.): Journal for Applied Mathematics and Mechanics (=  Issue 4/5 ). tape 44 , April 1964, p. 149–158 , doi : 10.1002/zamm.19640440402 ( wiley.com ).