directional quantization

Quantization of angular momentum along the quantization axis . The cones (and the plane) show the possible orientations (angles) of the angular momentum vector relative to the axis for and . ${\displaystyle z}$ ${\displaystyle J=2}$ ${\displaystyle m_{j}=-2,-1,0,1,2}$

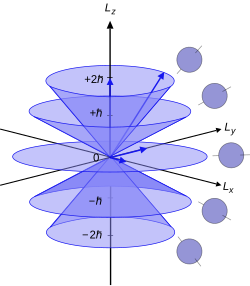
Directional quantization or directional quantization is the fact that the angle between the angular momentum vector of a quantum mechanical system and an arbitrarily chosen direction can only assume certain, discrete values. ${\displaystyle \theta _{m}}$

The states with well-defined angle between the angular momentum and a distinguished axis, the quantization axis , are also called on-axis aligned .

Affected are u.

• Spin and orbital angular momentum of free particles and
• without exception all free atoms , molecules etc. in their energy eigenstates .

Mathematical description

With a total angular momentum , whose absolute value is given by , the component of angular momentum can only assume values ​​along the chosen direction . ${\displaystyle {\vec {J}}}$ ${\displaystyle {\sqrt {J(J+1)}}\,\hbar }$ ${\displaystyle m_{j}\,\hbar }$

inside is

• ${\displaystyle J=0,\,{\frac {1}{2}},\,1,\,{\frac {3}{2}},\,\ldots }$the half or integer total angular momentum quantum number
• ${\displaystyle \hbar }$the (reduced) Planck constant
• ${\displaystyle m_{j}=-J,\,-(J-1),\,\ldots ,\,(J-1),\,J}$the directional quantum number of the total angular momentum.

The possible angles result in: ${\displaystyle \theta _{m}}$

${\displaystyle {\begin{alignedat}{3}-1&<\cos \theta _{m}&&={\frac {m_{j}}{\sqrt {J(J+1)}}}&&&<1\\\Rightarrow 180^{\circ }&>\theta _{m}&&=\arccos {\frac {m_{j}}{\sqrt {J(J+1)}}}&&&>0^{\circ }\end{alignedat}}}$.

They are symmetrical to 90°. Because 0° and 180° are excluded here, the angular momentum in the two states with the maximum component ( ) is often referred to as parallel or antiparallel to the axis. ${\displaystyle m_{j}{\mathord {=}}\pm J}$

The direction of the component of angular momentum perpendicular to the axis is not fixed in aligned states; rather, all directions (perpendicular to the axis) are equally probable. However, all states that the system can assume at all with the same internal state can be formed from the aligned states by quantum mechanical superposition . So you can z. For example, a state that is oriented along any other (also oblique) direction is always represented as a superposition of the states that are oriented along the originally chosen axis. ${\displaystyle 2J+1}$

story

Directional quantization was theoretically predicted in 1916 as part of the Bohr-Sommerfeld atomic model . It allows the quantum physical interpretation of the splitting of the energy levels in the magnetic field , as observed in the Zeeman effect . Directional quantization was first observed directly in 1922 by magnetic deflection of silver atoms with differently oriented angular momenta in the Stern-Gerlach experiment .

In both cases, the quantum numbers correspond to different energy levels in the magnetic field, from which the name magnetic quantum number and the choice of the letter are derived. ${\displaystyle m}$ ${\displaystyle m}$

See also

• spin polarization
• spin-orbit interaction
• nuclear magnetic resonance
• multiplicity