Spin polarization
In a collection of similar particles such as electrons , atoms or ions, there is spin polarization if the spin vectors of the particles are more or less aligned, i.e. the directions are not randomly distributed. In technical language z. B. in nuclear physics is usually simply referred to as polarization .
Basics
The axial vector of a spin described by the quantum number can adopt different directions with respect to a selected quantization axis (see direction quantization , multiplicity ). These are denoted by a "spin magnetic" quantum number :
In the simplest case , the two values and (multiplicity 2) result.
States that differ only in the value of are quantum mechanically different. But they usually have the same energy, so they are " degenerate ". In an ensemble of particles of the same kind, these states are therefore generally equally populated apart from random statistical fluctuations (the electrons and positrons of the beta radiation are an exception , see below).
A polarization, i.e. deviation from the uniform distribution , can be described in the case of spin 1/2 particles by the degree of polarization :
Here and are the numbers of particles with the two spin orientations (“up” and “down”) to the selected axis. The degree of polarization is also often referred to as “the polarization” for short. is 0 for an unpolarized ensemble and ± 1 for a maximally polarized ensemble, often expressed as ± 100%. Description by a polarization vector is also possible; this is the vector sum of all spins in the ensemble divided by the number of particles and is usually also normalized to the amount 1 for maximum polarization . For particles with a higher spin than 1/2, i.e. three or more possible orientations, the description of the polarization is more complicated and generally requires a tensor of the appropriate level.
Spin polarization is not a property of a single particle, but of the ensemble. To speak of a single “polarized particle” is pointless. In terms of quantum mechanics, spin polarization can be described using the density matrix formalism.
Spin polarization in a magnetic field
The spin of particles is associated with a magnetic moment . If the ensemble of particles is brought into a magnetic field , the energy of the individual state changes depending on the position in relation to the direction of the field, and the degeneration is reversed. Hence the term "magnetic" quantum number. The corresponding observable splitting of optical spectral lines is called the Zeeman effect .
Since the particles prefer to collect in states of lower energy, the magnetic field leads to a certain spin polarization without any further measures. However, this is usually low at ambient temperature because the magnetic energy differences are small compared to the thermal energy of the particles (this applies in particular to atomic nuclei with their small magnetic moments). Much higher polarizations can be achieved with special processes. This is called hyperpolarization in some, but not all, cases .
Spin-orbit interaction in scattering processes
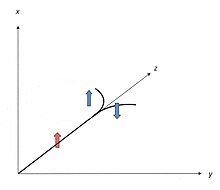
If a particle initially flying in a straight path is deflected with spin from its direction of flight, the interaction between spin and orbital angular momentum influences the movement, similar to that in atoms and atomic nuclei (see spin-orbit coupling ). For example, if the spin vector points in the -direction while the particle flies in the -direction, the vectors of spin and orbital angular momentum are antiparallel when deflected ( scattered ) in the -direction and parallel to each other in the - -direction (see sketch). The differential effective cross-section is therefore different for the same scattering angle, depending on whether the scattering takes place on the + side or on the - side . More generally: it depends not only on the scattering angle but also on the azimuth angle (see spherical coordinates ), the angle between the plane of the orbit and the xz plane . In this way, the scattering process represents an analyzer for a polarized particle beam , because two detectors set up symmetrically to the left and right of the plane register different numbers of particles. On the other hand, with an unpolarized beam, the particles that are scattered to a certain side are a more or less strongly polarized ensemble; the scattering process also acts as a polarizer.
Because of the conservation of angular momentum , the behavior of nuclear reactions is similar to that of scattering. Scattering and reaction experiments with observation of the polarization of the emitted particles or with a polarized beam or target are therefore an important means in nuclear physics for a more detailed determination of the spin-orbit interaction. Before it was possible to produce polarized particle beams or polarized targets, double- scattering experiments, in which the same particles passed through two scatters in a row, provided information on this. For them, the first scatter represented the polarizer, the second the analyzer.
The weak charge of the proton was measured precisely in a scattering experiment using a polarized 1.16 GeV electron beam . The fact that parity is not maintained only applies to weak interaction .
Establishing the spin polarization
Neutral matter
In solids, liquids or gases, polarization of the atomic nuclei is generated by means of a magnetic field, often with the help of low temperatures, in order to keep the thermal energy of the particles small (see Boltzmann distribution ). With this technique z. B. in the Wu experiment at 10 milli kelvin a degree of polarization of the cobalt -60 cores of about 60%.
Instead of a strong external field, the field caused by the electron spin in a paramagnetic ion can in some cases be used to polarize the nuclei , so that a relatively weak external field is sufficient to align the ions.
Another method is to align atoms by optical pumping with circularly polarized light and to use the coupling of the electrons with the nuclear moment (see hyperfine structure ).
Ion beams
Polarized ion beams for use in particle accelerators can be produced according to the further developed concept of the Stern-Gerlach experiment : from an atomic beam , e.g. B. hydrogen or deuterium , a polarized partial beam is obtained in the inhomogeneous magnetic field and then - in the simplest case - ionized in a weak magnetic field using the hyperfine splitting .
Another type of “polarized ion source ” uses the splitting of the energy levels through the Lamb shift .
Electron beams
Electrons in storage rings are polarized longitudinally through the emission of synchrotron radiation .
Neutrons
Polarized slow neutrons for neutron scattering are obtained by reflection on the aligned atoms of a ferromagnetic mirror (see neutron super mirror ).
Applications
- Spin-polarized neutrons can be used to study the magnetic structure of solids .
- In photoelectron spectroscopy , the spin polarization of the emitted electrons can provide information about the magnetic alignment of the sample and the polarization of the exciting radiation.
- In nuclear physics , scattering and nuclear reaction experiments with polarized particles help to investigate the details of certain states of the nuclei, since the cross sections of the processes depend on the spin alignment.
- It is possible that the reaction yield in nuclear fusion reactors can be significantly improved by using spin-polarized fuel.
- Substances with polarized atomic nuclei improve in certain nuclear magnetic resonance studies , e.g. B. in medicine, the sensitivity (see hyperpolarization (physics) ).
- The spin-polarized scanning tunneling microscopy allow a detailed analysis of the surface of magnetized materials.
- A temporally constant electron polarization is used in the read head of hard disks when reading via the magnetoresistive effect . In initial models, this polarization was only a few percent.
- A temporally coherent oscillating electron polarization can be detected in the Rabi oscillation in magnetic systems. It may be useful in quantum computers .
Electron and positron polarization during beta decay
The particles emitted during beta decay are spin-polarized along their emission direction. To put it clearly, z. B. the electrons from beta-minus decays, seen in their direction of flight, preferably counterclockwise ( left-handed electrons ). This is explained by the fact that the weak interaction responsible for the beta decay only generates chiral left-handed particles and chiral right-handed antiparticles, in so far as the mirror symmetry of the laws of nature is violated to the maximum (see parity violation ). This has the effect of a longitudinal spin polarization of the emitted particles. Theory and measurements show that the degree of polarization ( particle speed , speed of light ) is practically 100% for relativistic beta electrons and for neutrinos from beta decay.
literature
- H. Paetz gen. Schieck: Nuclear Physics with Polarized Particles. Heidelberg etc .: Springer, 2012. ISBN 978-3-642-24225-0 .
Individual evidence
- ^ JE Reimer: Nuclear hyperpolarization in solids and the prospects of nuclear spintronics. Solid State Nuclear Magnetic Resonance Vol. 37 (2010) pp. 3-12.
- ↑ z. B. generally not in connection with nuclear reactions, see e.g. Schieck (literature list).
- ↑ N. Bigelow, P. Nacher and M. Leduc: Accurate optical measurement of nuclear polarization in optically pumped He-3 gas. J. de Physique Vol. 2 (1992) pp. 2159-2179.
- ^ Bernard L. Cohen, Concepts of Nuclear Physics , New York, etc .: McGraw-Hill, 1971, p. 53.
- ^ The Jefferson Lab Q-weak Collaboration: Precision measurement of the weak charge of the proton. Nature Vol. 557 (2018) pages 207-211, doi: 10.1038 / s41586-018-0096-0 [1] .
- ^ EB Paul: Nuclear and Particle Physics. Amsterdam: North-Holland, 1969. p. 318
- ↑ G. Clausnitzer, R. Fleischmann and H. Schopper, Zeitschrift für Physik Volume 144 (1956) p. 336.
- ↑ LW Anderson and W. Haeberli (eds.): Polarized Ion Sources and Polarized Gas Targets (conference report, Madison, Wisconsin 1993). American Inst. Of Physics, 1994.
- ^ AA Sokolov, IM Ternov: On Polarization and Spin Effects in Synchrotron Radiation Theory. So V. Phys. Docl. Volume 8, p. 1203 (1964).
- ↑ H. Paetz gen. Schieck: The status of polarized fusion , Eur. Phys. J. 44 A (2010) pp. 321-354.
- ↑ Jörn Bleck-Neuhaus: Elementary Particles . From the atoms to the standard model to the Higgs boson. 2nd, revised edition. Springer, Berlin Heidelberg 2013. Page 546 f.