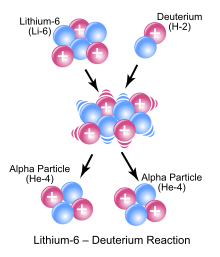Nuclear reaction
A nuclear reaction is a physical process in which an atomic nucleus changes its state or its composition when it collides with another atomic nucleus or particle. Often the elastic collisions of nuclei are not counted, because only the impulses of the two collision partners change, sometimes not the inelastic collisions, in which one of the collision partners is additionally put into an excited state . In the other cases - the nuclear reactions in the literal sense of the word - the nuclei change their composition by releasing or absorbing particles. However, the total number of existing nucleons is always retained, in most of the cases considered also the neutrons - and the number of protons each separately.
Radioactive decay is not one of the nuclear reactions , because here the nuclear transformation takes place spontaneously, i.e. it is not triggered by a shock.
Nuclear physics and particle physics are primarily concerned with research into nuclear reactions . Nuclear reactions play an important role in the formation of nuclides, see Sect. Astrophysics , cosmochemistry . There are applications for B. in energy technology (see nuclear reactor , fusion reactor ) and medical technology (production of radionuclides for nuclear medicine and radiation therapy ).
Certain restrictions result from the conservation of momentum and energy in the nuclear reactions. They are described in the article Kinematics . Other conserved quantities such as the baryon number also play a role.
history
Starting in 1911, Ernest Rutherford used alpha particles from a radioactive substance in his scattering experiments, in which he observed their elastic scattering on gold atomic nuclei. The first observation of a nuclear reaction in the narrower sense, also by Rutherford, dates from 1919: Alpha particles were shot through nitrogen, which behind it also gave signals of protons on the zinc sulfide screen, which served as a scintillator (reaction: 14 N + α → 17 O + p).
Further research into and use of nuclear reactions was based predominantly on artificially accelerated projectile particles and was therefore closely linked to the development of particle accelerators . In 1930, John Cockcroft and Ernest Walton succeeded in providing the first evidence of a nuclear reaction triggered by artificially accelerated particles - at the time proudly referred to as nuclear shattering . They irradiated lithium with protons with a kinetic energy of 300 keV ; 4 helium atomic nuclei (alpha particles) were observed as reaction products . So it was the reaction 7 Li + p → 2 4 He. The energy and mass balance determined by them became the first experimental proof of the “ conversion of mass into energy ” according to Einstein's equation E = mc 2 .
Formula notation and examples
In the symbolic picture shown as an example, a 6 Li nucleus and a deuterium nucleus (a deuteron ) react and form the intermediate nucleus 8 Be, which immediately breaks down into two alpha particles .
A nuclear reaction can be represented and verified by a formula similar to a chemical equation . Nuclear decays can be represented similarly, but then there is only one nucleus on the left. Every particle that takes part in the reaction is written with its chemical symbol , with the mass number at the top left and the atomic number at the bottom left. Since the atomic number is clearly defined by the chemical symbol, it can also be omitted.
The formula for the example shown is
or simplified
- .
The neutron is written as n, the proton can be written as 1 H or p. Some particles appear in so many reactions under consideration that they are usually abbreviated. For example, the 4 He core is designated with the Greek letter α. Deuterons (heavy hydrogen , 2 H) are denoted by d.
In many reactions of interest, a relatively light particle ( nucleon or light nucleus, the projectile ) meets a relatively heavy nucleus, a particle of the same “light” class (the ejectile ) is emitted, and another nucleus remains. In these cases, the reaction can be simply written as follows
- .
The starting core is often referred to as the target core (from English target 'target').
Projectile or ejectile are mostly protons , deuterons , helium nuclei, tritons , neutrons , gamma quanta , etc.
For example, with particle symbols, the formula is
- ,
with omitted ordinal numbers
or in compressed form
- .
Further examples
From an atomic nucleus of silver -107, a neutron is captured and a γ-quantum emitted, silver-108:
- 107 Ag (n, γ) 108 Ag
14 N is converted into 14 C by a neutron of cosmic radiation (this process continuously generates 14 C, the basis of radiocarbon dating ):
- 14 N (n, p) 14 C
A lithium -6 nucleus absorbs a neutron and is converted into a triton and a helium-4 nucleus:
- 6 Li (n, t) 4 He
The reaction types listed in the examples (regardless of the target nuclide) are briefly referred to as (d, α), (n, γ), (n, p) or (n, t) reactions.
Special types of nuclear reactions and special cases
The compressed notation is also used for scattering processes . For example, 12 C (n, n) 12 C or 12 C (n, n) for short stands for the elastic scattering of a neutron on a carbon-12 nucleus. Inelastic scattering is indicated by a line on the precipitating particle, e.g. B. 12 C (n, n ') or 12 C (α, α').
In the case of the (n, ) reaction, which is particularly important with thermal neutrons , one speaks of neutron capture or neutron attachment, with (p, ) correspondingly of proton attachment .
Special cases with regard to the notation are induced nuclear fission and spallation . A certain cleavage reaction, e.g. B. the first known, discovered by Otto Hahn and co-workers, can be written as 235 U + n → 140 Ba + 94 Kr + 2n or 235 U + n → 140 Ba + 93 Kr + 3n , depending on the number of neutrons released (See the discovery of nuclear fission ). However, if - as is often the case in practice - it is not interesting which of the many possible pairs of fission products is created and how many new neutrons are emitted, 235 U (n, f) is simply written (f for fission 'fission') .
In the spallation reaction, triggered by a high-energy particle, a core is broken into many fragments; here the notation in the formula style mentioned makes little sense.
Reaction mechanisms
Nuclear reactions are mostly based on the strong and the electromagnetic interaction , in certain cases only the latter alone. The weak interaction plays practically no role in nuclear reactions in the terrestrial environment, but is important in astrophysical processes; in such cases there are also conversions of neutrons into protons or vice versa.
The experimental observations suggest that nuclear reactions can proceed in very different ways depending on the nuclei / particles involved and depending on the impact energy. The types described below, inter-nuclear reaction and direct reaction, are only idealized borderline cases; reactions actually observed are mostly mixtures of the types; H. the resulting particles, radiations, etc. come partly from the various processes.
Inter-nuclear reactions
If the impact energy is small compared to the binding energy of a proton or neutron in the nucleus (this averages around 9 MeV across all nuclides ), the observations can often be explained well by the inter-nucleus model: The two colliding particles / nuclei combine to form a new nucleus which then breaks down into two or more parts regardless of how it was created. Typical characteristics of an inter-nuclear reaction are:
- Resonances in the excitation function
- Forward-backward symmetry, i.e. H. Mirror symmetry around the 90-degree direction of the angular distribution considered in the center of gravity system
Direct reactions
With higher impact energies, however, direct reaction mechanisms come to the fore. These include As the stripping reaction (Engl. Stripping , stripping), the most in deuterons is important as bullets. The relatively weakly bound deuteron breaks into its two components, the neutron and the proton; the one that has come close enough to the target core is absorbed while the other one flies on. So there is a (d, n) - or (d, p) - reaction. The (d, np) reaction is also possible as a direct reaction ( deuteron breakup ) if the deuteron breaks in the force field of the target nucleus, but no absorption occurs. Stripping reactions also play, albeit with a lower probability, e.g. B. as ( 3 He, d) -, ( 6 Li, d) reactions etc. a role.
Other direct reactions are the pickup reaction (engl. Pick up , take up ',' take '), wherein the Geschossteilchen absorbs a nucleon from the target nucleus and entrains, z. B. a (p, d) - or (d, 3 He) reaction, and the kickoff reaction (English kick off , push away), z. B. of type (n, p). (n, p) reactions carry z. B. is essential for material activation by fast neutrons in fusion reactors .
Typical for direct reactions are
- an excitation function that increases monotonically with the impact energy over a larger area
- a strong preference for small reaction angles, ie a “forward peak” of the angle distribution.
As mentioned above, all reaction types possible as a direct reaction are also possible as an intermediate nuclear reaction. Often the two basic types overlap, e.g. B. an excitation function with a smooth, gradually rising ground and individually seated resonances.
Q-value and energy balance
Since the binding energy per nucleon is different in different nuclei, some nuclear reactions are exothermic . H. they release energy in addition to the existing kinetic energy. Others are endothermic , that is, they absorb energy; this must then be "brought along" as kinetic energy by one or both reaction partners ( threshold energy ) so that the reaction is possible (that is, its effective cross-section is different from zero). In nuclear physics, energies are usually given in mega electron volts (MeV).
The excess energy of exothermic reactions can be released as kinetic energy of the reaction products and / or as gamma radiation .
Exothermic reactions can also require activation energy . This always applies to reaction partners charged with the same name , because the electrical repulsion must be overcome; because of the tunnel effect , however, this activation energy is not sharply defined. If a collision partner is uncharged (neutron or photon), the electrical repulsion does not play a role, but even then a minimum energy can be necessary to achieve a sufficiently high excitation state of the intermediate nucleus. An example of this is the neutron-induced fission of nuclei with an even number of neutrons .
When notation according to a chemical equation, the energy gain or loss Q can also be specified:
- Initial core + projectile → end core + Ejektil + Q .
The last of the above examples, the breeding process in the blanket of a fusion reactor , is written like this:
This amount of energy (usually just called “ Q value” in nuclear physics ) is positive for an exothermic reaction and negative for an endothermic reaction. It indicates the difference between the total kinetic energy before and after the reaction and can be determined according to E = m c 2 from the difference in the total masses on the start side and the end side. The mass difference in the example given above is
The atomic mass unit u corresponds to the amount of energy
- ,
hence the Q value results to
- , as you can read above.
In the nuclear masses one can omit the part ( is the respective number of nucleons ) from the start, because it stands out in the difference formation anyway. Instead of the masses, one uses the excesses of mass and thus avoids the determination of a small difference between large numbers. This is a useful relief for non-digital calculations.
Statistical fluctuations
If a given, constant stream of projectile particles hits a given target, the nuclear reaction rate (number of reactions per time interval) can be calculated from the cross section of the reaction of interest . However, this is only a statistical mean. The actual number of reactions observed in a certain period of time fluctuates randomly around this mean value; the frequency with which the individual possible numbers occur follows the Poisson distribution . Thus radiation from a nuclear reaction (with a constant reaction rate) is statistically distributed in the same way as that from a radioactive source.
Web links
- Table of atomic masses
- Script for calculating energy balances of nuclear reactions
- Q Value Calculator for the Q value calculation
Individual evidence
- ↑ E. Rutherford: Collision of α particles with light atoms. IV. An abnormal effect in nitrogen . In: Philosophical Magazine . tape 37 , 1919, pp. 581-587 . ( Publication text )
- ↑ Eric B. Paul, Nuclear and Particle Physics, North-Holland Publ. Comp., 1969
- ↑ Bethge, Walter, Wiedemann: Nuclear Physics . 2nd edition, Springer Verlag 2001