Strong interaction

The strong interaction (also strong force , gluon force , color force ) is one of the four basic forces of physics . It explains the bond between the quarks in the hadrons . Their exchange particles are the gluons .

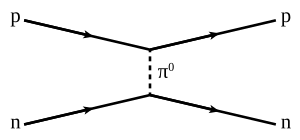
Before the introduction of the quark model, only the force of attraction between the nucleons of the atomic nucleus was referred to as the strong interaction . H. Protons and neutrons . Even today, the strong interaction often only refers to this residual interaction , also called nuclear force or strong nuclear force for historical reasons .

Feynman diagrams for the fundamental coupling possibilities of the strong interaction, a) emission of a gluon, b) splitting of a gluon c), d) "self- coupling " of the gluons.

Bond between quarks

Interaction within a neutron (example). The gluons are shown as points with the color charge in the center and the anti- color on the edge.

According to quantum chromodynamics (hereinafter: QCD), the strong interaction - like the electromagnetic and the weak interaction - is described by the exchange of gauge bosons . The exchange particles of the strong interaction are known as gluons , of which there are eight types (different color charge states). The gluons transfer a color charge between the quarks. A gluon can interact with other gluons and exchange color charges.

Potential between two quarks as a function of their distance. In addition, the mean radii of various quark-antiquark states are marked.

The attraction between quarks remains constant even with increasing distance, unlike z. B. in the case of the Coulomb force , in which it becomes easier and easier to separate two attractive particles as the distance increases. It is roughly comparable to a rubber cord or a tension spring . If the distance becomes too large, the rope “breaks” in this analogy and a meson is formed by generating a quark-antiquark pair from the vacuum. If the distance is small, the quarks can be viewed as free particles ( asymptotic freedom ). With a greater distance, the increasing interaction energy causes the quarks to lose the character of independent particles, which is why they cannot be observed as free particles ( confinement ).

Bond between nucleons

Although nucleons always have the color charge zero, there is a residual interaction or nuclear force between them (distantly comparable to the Van der Waals forces , which can be viewed as residual electromagnetic interactions between electrically neutral atoms and / or molecules ).

The range of attraction through the residual interaction is around 2.5  femtometers (fm). With this value of the distance , it is as strong as the electrical repulsion ( Coulomb force ) between the protons and with shorter distances it is stronger than the Coulomb force. Above this distance, on the other hand, the attraction decreases faster than the Coulomb force, which decreases proportionally to . This interplay of the two basic forces explains the cohesion and the size of the atomic nuclei. B. also the splitting of heavy nuclei . ${\displaystyle r}$ ${\displaystyle 1/r^{2}}$

The nuclear force acts repulsively at very short distances, corresponding to a hard core of 0.4 to 0.5 fm. It is also spin-dependent: it is stronger for parallel spins than for antiparallel, so that the deuteron (consisting of a neutron and a proton) is only bound for parallel spins (total spin 1), and diproton and dineutron (with antiparallel spins due to of the Pauli principle ) are not bound. In addition to the central potential component and the spin-spin interaction component, it also has a tensor component and a spin-orbit component.

Before the introduction of the quark model, the residual interaction and its short range were explained with an effective theory : a Yukawa interaction between nucleons and pions ( pion exchange model ). The short range is explained by the non-zero mass of the pions, which leads to an exponential attenuation in the Yukawa potential at greater distances. In addition, the exchange of further mesons was taken into account in the nucleon-nucleon potential models (such as the rho meson ). Since it has not yet been possible to calculate the nuclear force with QCD, various phenomenologically adapted potentials based on meson exchange models (such as the Bonn potential) are used in the description of nucleon-nucleon scattering.

Explanation of the residual interaction

Feynman diagram of a strong proton - neutron interaction mediated by a neutral pion . The time axis runs from left to right.

The same diagram shown with the individual constituent quarks to show how the fundamental strong interaction creates a "nuclear force". Straight lines are quarks, multicolored loops are gluons (carriers of the basic force ). Other gluons, which hold proton, neutron and pion together (in "flight"), are not shown.

An animation of the interaction, the two small colored dots are gluons. Anti-colors can be seen in this diagram . ( larger version )

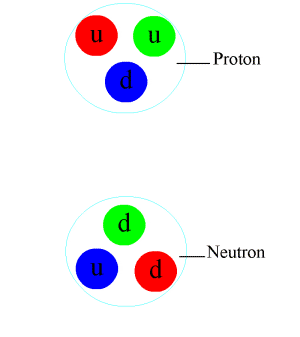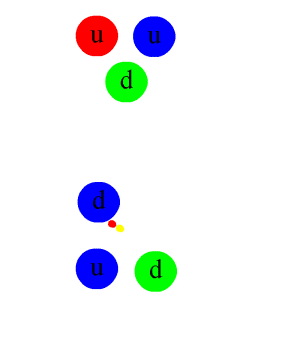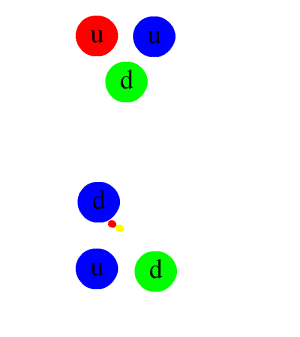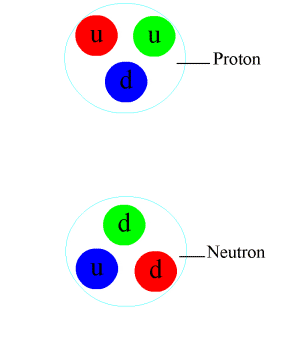
The repulsive potential between atoms at small distances is a consequence of the Pauli principle for the electron states. When two nucleons with six quarks approach each other, each quark has considerably more degrees of freedom in the lowest state (orbital angular momentum l = 0): in addition to spin (2 states), there is also a color charge (3 states) and isospin (2 states), i.e. a total of 12 on the the six quarks can be distributed according to the Pauli principle. The Pauli principle is not directly responsible for the repulsion, which is noticeable below about 0.8 fm. Rather, the reason lies in the strong spin-spin interaction of the quarks, which is evident in the fact that the delta resonance (with parallel spins of the three quarks) has a mass about a third higher than the proton. If the spins of the quarks are parallel to one another, the potential energy of the system increases. This also applies to overlapping nucleons, and more so, the closer the distance between the nucleons is. If the quarks try to minimize their chromomagnetic energy by reversing the spin , this can only be achieved by transitioning to an energetically higher orbital angular momentum state (l = 1).

With an even greater distance from each other, the nucleons enter the attractive part of the strong interaction. The quark-quark exchange (two quarks are assigned to both participating nucleons at the same time), which is expected in analogy to the covalent bond , plays less of a role here than that of color-neutral quark-antiquark pairs (mesons) from the sea ​​quark portion the nucleon wave function in the QCD.

A complete description of the nuclear force from quantum chromodynamics is not yet possible.

Classification of the strong interaction

Fundamental interactions and their descriptions
	Strong interaction	Electromagnetic interaction	Weak interaction	Gravity
classic		Electrostatics & magnetostatics , electrodynamics		Newton's law of gravitation , general relativity
quantum theory	Quantum ( standard model )	Quantum electrodynamics	Fermi theory	Quantum gravity  ?
		Electroweak Interaction ( Standard Model )
	Big Unified Theory  ?
	World formula ("theory of everything")?
Theories at an early stage of development are grayed out.

literature

• Manfred Boehm , Ansgar Denner , Hans Joos : gauge theories of the strong and Electroweak interaction , Teubner-Verlag, Stuttgart 2001, ISBN 978-3-519-23045-8 (original German: Becher Böhm-Joos, gauge theories of the strong and electroweak Interaction ) - a standard work for theory
• Bogdan Povh , Klaus Rith , Christoph Scholz, Frank Zetsche Particles and Cores , 8th edition, Springer Verlag 2009
• Wolfgang Wild core forces and core structure , part 1,2, Physikalische Blätter 1977, pp. 298, 356, part 1 , part 2

Web links

• Marc Gänsler: The strong interaction . In: Introduction: The 4 Fundamental Forces of Physics , accessed January 30, 2009.
• Gluons and the strong force . DESYs Kwork Quark, "Particle Physics for Everyone"

Individual evidence

1. ↑ The total wave function is antisymmetric and therefore, since the color component is always antisymmetric (total color charge zero) with a symmetrical space wave function (orbital angular momentum 0), the spin-isospin component must also be symmetrical
2. ↑ Discussion after Povh, Rith, Schulze, Zetsche Particles and Kerne , p. 250f, there after Amand Fäßler