In spherical or spatial polar coordinates , a point in three-dimensional space is specified by its distance from the origin and two angles .
In the case of points on a spherical surface ( sphere ) around the coordinate origin , the distance from the center of the sphere is constant. Then only the two angles are variable; they are then called spherical coordinates or spherical surface coordinates .
The term “spherical coordinates” can be seen as a generic term for the general case and the spherical coordinates. Like cylindrical coordinates, spherical coordinates are a generalization of the plane polar coordinates to three-dimensional Euclidean space . They can also be generalized further to spaces of any finite dimension.
Usual convention
definition
A spherical coordinate system in three-dimensional Euclidean space is determined by the choice
- of a center (origin),

- a directed straight line through the center (polar axis), which indicates the pole direction (or zenith direction), and this defines the equatorial plane which runs through the center orthogonally to the pole direction, and
- a reference direction in the equatorial plane .
A Cartesian coordinate system is often used at the same time . Then the origin of the Cartesian coordinate system is typically chosen as the center, the z- axis as the polar axis (and thus the xy -plane as the equatorial plane) and the x -axis as the reference direction.
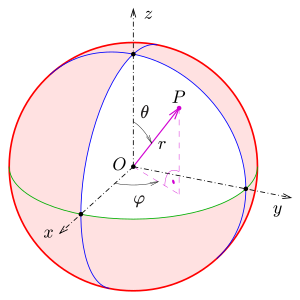
In the version of spherical coordinates that is common in mathematics and physics, a point is defined by the following three coordinates :

-
 , the radius , is the distance of the point from , this defines the sphere surface on which is located.
, the radius , is the distance of the point from , this defines the sphere surface on which is located.


-
 or , the polar angle or pole distance angle , is the angle between the pole direction and the segment , counted from to (0 ° to 180 °), which defines the location of the point on a circular line on the spherical surface .
or , the polar angle or pole distance angle , is the angle between the pole direction and the segment , counted from to (0 ° to 180 °), which defines the location of the point on a circular line on the spherical surface .




-
 or , the azimuth angle , is the angle between the reference direction and the orthogonal projection of the line , counted from to (−180 ° to 180 °) or from 0 to (0 ° to 360 °) counterclockwise. This clearly defines the location of the point on the circular line.
or , the azimuth angle , is the angle between the reference direction and the orthogonal projection of the line , counted from to (−180 ° to 180 °) or from 0 to (0 ° to 360 °) counterclockwise. This clearly defines the location of the point on the circular line.





The illustration opposite shows a point with spherical coordinates . The two angle sizes and are also referred to as angle coordinates .




Conversions
A point in three-dimensional Euclidean space is assigned to each coordinate triple (parameterization). If you choose a Cartesian coordinate system as above, the assignment can be described by the following equations :


Any number values can be used for , and in these equations . So that the spherical coordinates are clearly determined, the value range of the coordinates must be restricted. Usually the radius is limited to non-negative values, the angle to the interval or [0, 180 °] and the angle either to the interval or (−180 °, 180 °] or the interval or [0, 360 °) . Even then there are degenerate points for which the angular coordinates are not unique. For points on the z axis, the angle is not fixed, so it is arbitrary. For the origin is also arbitrary. In order to achieve clarity, one can define points for these points and additionally for the origin .





![[0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)

![(- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)





For the other points, the spherical coordinates can be calculated from the Cartesian coordinates using the following equations:





The equations given for the angle apply when choosing between and . If you choose between 0 and , they can be modified appropriately.






In analysis and its applications, spherical coordinate angles are usually given in radians .
Applications
Spherical coordinates are often used when examining systems that are rotationally symmetrical about a point. Examples are: Volume integrals over spheres, the description and investigation of rotationally symmetrical force fields , such as B. the gravitational field of a spherical celestial body, the electric field of a point charge or a charged sphere. The sizes considered then do not depend on the angular coordinates, which simplifies many formulas. Important partial differential equations such as the Laplace equation or the Helmholtz equation can be solved in spherical coordinates by separating the variables .
Other conventions
The above choice of coordinates is international consensus in theoretical physics . Sometimes the characters and are used in the opposite sense, especially in American literature.


The polar angle is not the latitude , but blends with the Colatitude identify. The geographical latitude is the angle between the equatorial plane and the position vector and has values between and . If it is marked with , then it is . On the other hand, the one used above can easily be equated with the geographical longitude east of Greenwich (see geographical coordinates ).







The above construction is in some respects inconsistent with the construction of the plane polar coordinates. For some problems it is more practical to use the representation



to use. In this representation corresponds to the geographical latitude.

The reverse transformation of the point or vector into the angle components then takes place with


-
 ,
,
whereby .

Transformation of differentials
Jacobian matrix
The local properties of the coordinate transformation are described by the Jacobi matrix . For the transformation of spherical coordinates into Cartesian coordinates this is

The corresponding functional determinant is:

The easiest way to calculate the Jacobi matrix of the opposite transformation is as the inverse of :


Some components of this matrix are fractions , at whose denominators one recognizes the ambiguity of the polar coordinates at and at (i.e. or ). The representation in Cartesian coordinates is less common:





Differentials, volume element, surface element, line element
The Jacobi matrix allows the conversion of differentials to be written clearly as a linear map:

respectively
-
 .
.
The volume element can be made particularly simple with the aid of the functional determinant

convert:
-
 .
.
Differentiation gives the surface element on a sphere with a radius


-
 .
.
The line element is calculated according to


Metric and rotation matrix
The absence of mixed terms in the line element reflects that the metric tensor

has no off-diagonal elements even in spherical coordinates.
The metric tensor is obviously the square of the diagonal matrix
-
 .
.
With the help of this matrix the Jacobi matrix can be written as, whereby the rotation matrix


is.
Transformation of vector fields and operators
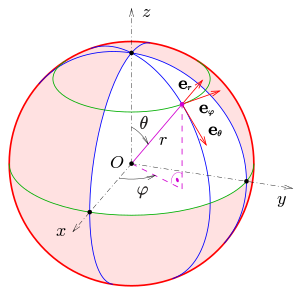
Spherical coordinates with an associated orthogonal base that is dependent on the location

In the following, the transformation of vectors and differential operators is shown as an example. The results are preferably written in compact form using transformation matrices. Most statements and formulas only apply to points outside the z -axis for which the Jacobi determinant is not equal to zero.
Transformation of the vector space basis
The base vector for the coordinate specifies the direction in which a point moves when the coordinate is changed by an infinitesimal amount :





-
 .
.
From this you get
-
 .
.
To get an orthonormal basis, you have to normalize to the length :


-
 .
.
The basis vectors and are obtained in the same way :




Written as column vectors :

These basis vectors form a legal system in the sequence .

The associated directions are also called radial , meridional and azimuthal . These terms not only play a central role in astronomy and the geosciences (e.g. geography , geology or geophysics ), but also in mathematics , physics and various engineering sciences , for example in the emission of electromagnetic waves (" Hertzian dipole ") an antenna spanned in the z direction, where the radiation takes place in the radial direction, while the electric or magnetic field oscillates in the meridional or azimuthal direction.
With the help of the rotation matrix introduced above , the transformations can also be represented in compact form:

-
 .
.
In the opposite direction the equations are then:
-
 .
.
(It is used that is orthogonal and therefore .)


Transformation of a vector field
A vector , as a geometric object, must be independent of the coordinate system:

This condition is met by
-
 respectively .
respectively .
Transformation of the partial derivatives
The partial derivatives transform like the basis vectors, but without normalization. You can calculate exactly as above, only you omit the point in the numerator (in fact, in the modern formulation of differential geometry, the coordinate basis vectors of the tangent space and the partial derivatives are equated) and the Jacobi matrix is used instead of the rotation matrix . So the transformation is:



-
 ,
,
and in the opposite direction
-
 .
.
Transformation of the Nabla operator
The Nabla operator has the simple form only in Cartesian coordinates

-
 .
.
Both the partial derivatives and the unit vectors have to be transformed in the manner derived above. One finds:
-
 .
.
In this form, the transformed Nabla operator can be used directly to calculate the gradient of a scalar field given in spherical coordinates.
In order to calculate the divergence of a vector field A given in spherical coordinates , however, it must be taken into account that not only acts on the coefficients , but also on the basis vectors implicitly contained in A.



In order to calculate the rotation of a vector field A given in spherical coordinates , the same must be taken into account:

Transformation of the Laplace operator
If one uses the gradient operator as the vector field A in the divergence formula, one finds the Laplace operator
-
 .
.
or.
-
 .
.
Generalization to n-dimensional spherical coordinates
A generalization of spherical coordinates to dimensions:


The angles develop according to:

Renumbering gives a recursion formula for the angles:

What the following angles result from:

with and


The radius is:

A case distinction provides the appropriate angle to the given Cartesian coordinate using an arctangent , where :


It is noticeable that there is always a two-dimensional vector for .


Jacobian matrix
The Jacobi matrix of the spherical coordinates is with respect to the numbering given above:

Their determinant is:

The integral over the amount of this determinant can be given with the gamma function .


This corresponds to the spherical volume of a -dimensional hypersphere :


Examples
2D:

3D:

4D:

example
Assignment using the example with the common coordinate axes :



The angles are then:

Web links
Individual evidence
-
↑ Richard Doerfling: Mathematics for engineers and technicians. Oldenbourg Verlag, page 169
-
↑ FW Schäfke: Introduction to the theory of the special functions of the special functions of mathematical physics. Springer, 1963, ISBN 978-3-642-94867-1 , page 129
-
↑ a b Lothar Papula : Mathematics for engineers and natural scientists. Volume 3: Vector analysis, probability calculation, mathematical statistics, error and compensation calculation. 4th improved edition. Vieweg + Teubner, Wiesbaden 2001, ISBN 3-528-34937-9 .
-
↑ a b script ( memento of the original from December 17, 2012 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 59 kB) at the Technical University of Munich
 @1@ 2Template: Webachiv / IABot / www-m8.ma.tum.de
@1@ 2Template: Webachiv / IABot / www-m8.ma.tum.de
-
↑ spherical coordinates . Mathematics online lexicon of the University of Stuttgart. Authors: App / Höllig
















![[0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![(- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)































































































