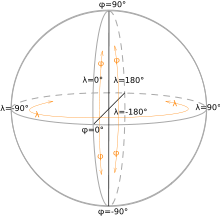
Geographic coordinates
The geographical coordinates are spherical coordinates with which the position of a point on the earth's surface can be described. The latitude is measured from the equator to the north (0 ° to 90 ° north at the north pole) and south (0 ° to 90 ° south at the south pole), the longitude from the prime meridian from 0 ° to 180 ° to the east and from 0 ° to 180 ° to the west. Circles of latitude (lines of constant latitude) run parallel to the equator , longitudes (lines of constant length) through the north and south poles .
Coordinate system
The graticule of the earth is an imaginary coordinate system on the earth's surface with circles of longitude and latitude intersecting at right angles. It is used to determine geographical location , that is, to determine a location. The latitudes are counted from the equator , the poles are at 90 ° north and south, the longitudes are counted from an arbitrarily defined prime meridian to the east and west up to 180 ° each. The definition of the angles is the opposite of the spherical coordinate system commonly used in mathematics .
Until the 20th century, in addition to the Greenwich meridian used today, different prime meridians were in use in various countries, e.g. B. the Ferro-Meridian and the Meridian of Paris .
When specifying coordinates, please note that the earth is not a sphere, but rather resembles an ellipsoid . This causes a shift of up to 20 km. Due to increasing knowledge about the shape of the earth and the gravitational field ( geoid ), nationally different references were used. Coordinates therefore always have a specific reference system. Internationally today the World Geodetic System 1984 (WGS84) is mostly used.
Representation of geographic coordinates

Geographic coordinates can be represented in three number formats:
- Traditionally they are given in the sexagesimal format; H. 1 degree is divided into 60 minutes , 1 minute again into 60 seconds (example: 46 ° 14′06.70 ″ N 8 ° 0′55.60 ″ E). Typographically, the minutes and seconds are denoted by a prime or double prime .
- In the second representation, the minutes are written in decimal form, the specification of seconds is unnecessary. 0.1 ′ corresponds here to 6.0 ″.
- In the third representation the degrees are shown in decimal form. Here 0.1 ° corresponds to 6.0 ′. The desired accuracy can be achieved with any number of decimal places.
The latitude values range from 90 ° S to 90 ° N and the longitude values are between 180 ° W and 180 ° E. To avoid misunderstandings, be in the aviation always two, the latitudes and longitudes three digits indicated. The approach map on the right shows an approach to Zurich. The waypoint AMIKI is indicated there as 47 ° 34.4'N 009 ° 02.3'E. The angular minutes and possibly the angular seconds are also given in two digits.
The table shows the coordinates of a historic building in reference to WGS84 as an example . The four examples describe the same point in the different spellings. In the illustration, the letter h is a placeholder for the information about the direction NS, WO. Often in German texts an E for “East” is written instead of the O for Osten . The direction of the compass can be given before or after the digits. The letters d , m and s stand for degrees, minutes and seconds.
In the fourth (decimal) notation, the latitude range is between −90 ° and + 90 °, the longitude range between −180 ° and + 180 °. The cardinal points N-S and EW are omitted here. Northern latitudes are positive and southern latitudes negative. Eastern longitudes are positive and western longitudes are negative. In order not to confuse the latitudes and longitudes, they have to be called " Latitude (Latitude, Lat) " and " Longitude (Longitude, Long) ". This notation is shown in the table on the fourth line.
| presentation | example | description |
|---|---|---|
| hddd ° mm ′ ss.ss ″ | N46 ° 14′06.70 ″ E008 ° 00′55.60 ″ | Specification in degrees (°), minutes (′), seconds (″) and decimal seconds |
| hddd ° mm.mmm ′ | N46 ° 14.11182 ′ E008 ° 00.92670 ′ | Specification in degrees (°), minutes (′) and decimal minutes |
| hddd.ddddd ° | N46.235197 ° E008.015445 ° | Specification in degrees (°) and decimal degrees |
| ± ddd.ddddd ° | Lat = 46.235197 ° Long = 008.015445 ° | Specification in ± degrees (°) and decimal degrees |
The format of the display of the geographical coordinates can be freely selected in most GNSS devices. In the historical Swiss reference system CH1903 , the same building has the coordinates y = 644496, x = 120581.
cards
In the 18th and 19th centuries, the geodesists compensated for larger regional deviations of the earth's shape from the ideal ellipsoid by calculating an adjacent ellipsoid in the area in question , which "hugs" the earth's surface in the area in question. The center of such an ellipsoid did not coincide with the center of mass of the earth, but the axis of rotation was parallel to the earth's axis. The coordinate system is “shifted” and “bent” compared to other such ellipsoids. Dozens of geodetic systems (reference systems for maps) were created. With the development of satellite navigation , a worldwide uniform system had to be created, the current WGS84 .
In maps or nautical maps, which are almost always based on earlier systems, an indication in a wrong reference system (e.g. entering a GPS position) could cause an error of several hundred meters if the reference ellipsoid (also map date, reference system) of the indication is not is the same as that of the card. Therefore, with exact coordinates (rule of thumb: if an accuracy better than 1 km or better than 1 arc minute is desired) the reference system should also be given.
Coordinates can be converted from one system to another with the help of suitable transformation software. Such software must contain the parameters that define the deviation of the reference systems from each other or from the WGS84 with the highest possible accuracy.
Aviation and nautical
More precise position information is required in aviation and nautical science . Here geographical latitude and longitude are given in degrees and minutes, e.g. B. Zugspitze Lat = 47 ° 25 'N or North, Lon = 010 ° 59' E or East.
- Arc minutes are further subdivided in decimal.
- According to DIN 13312, valid for aviation and seafaring , the geographical latitude is abbreviated as Lat or older also φ, the geographical longitude with Lon or λ. B and L do not conform to the standard.
- One minute of latitude corresponds to a distance of approx. 1852 m on the surface of the earth and defines the length of one nautical mile .
- The distance, which corresponds to one minute of length, is also 1852 m at the equator, but decreases towards the pole with the cosine of the geographical latitude down to zero. So it is dependent on the width. Within Europe, the distance is between 1.0 km and 1.5 km (see also expansion ).
Surveying
In surveying , centimeter accuracies are required - therefore, specifying arc seconds is not sufficient, as one arc second (1 ″) corresponds to about 31 m (width specification) or 20 m (length specification in Europe). Therefore, the decimal notation has established itself internationally. In Germany, the location of the fixed points could be specified to the millimeter as Gauss-Krüger coordinates , based on the Bessel ellipsoid , or in the GDR from the 1950s onwards, based on the Krassowski ellipsoid . Since the 1990s, there has been a changeover to UTM coordinates in the ETRS89 system in Germany , based on the GRS80 ellipsoid.
Natural, astronomical, ellipsoidal, geodetic coordinates
The natural coordinates (astronomical latitude φ and astronomical longitude λ) can be determined by astronomical location determination. They relate to the actual direction of the perpendicular at the measuring point. The ellipsoidal coordinates (B, L - also called geodetic coordinates), on the other hand, relate to the normal direction of the reference ellipsoid used. The difference between the perpendicular direction and the ellipsoid normal is usually less than 10 ″ and is referred to as the perpendicular deviation . As a rule, neither the plumb direction nor the ellipsoid normal run through the center of the earth.
With low accuracy requirements z. B. for map displays on very small scales, the earth's body is approximated by a sphere for simplification. In this case, latitude and longitude correspond to spherical coordinates . Only then is the width of the angle in the center of the earth between the equator and the point sought.
history
The graduation as the division of the full angle of the circle into 360 ° goes back to the astronomers Hypsicles of Alexandria ("Anaphorikos", 170 BC) and Hipparchus of Nicaia (190-120 BC).
Already Claudius Ptolemy used in his Geographike Hyphegesis around 150 AD a graticule with longitudes and latitudes. Its zero meridian was the ferro meridian, which was predominantly used until the 19th century, through the westernmost land point known at that time. Because his calculation of the circumference of the earth is far too small (about 30,000 km instead of 40,000 km), his information on geographical longitude does not differ by 18 ° 3 ′, but in Central Europe by a good 24 ° from the information relating to Greenwich . For reasons that are not clearly apparent, its width specifications are greater than the correct ones. On the one hand, this fits Ptolemy's too small earth diameter, on the other hand, if the distance between the sun and the earth was set too small of only 1210 earth radii from the position of the sun, it should have been concluded that the distance from the equator was too small.
After the rediscovery of Geographike Hyphegesis and its translation into Latin in the early 15th century, the Ptolemaic degree system quickly caught on.
Duarte Pacheco Pereira (1469–1533) improved the ancient measurement methods for global navigation anchored in the Azores . With the division of the globe into a Spanish and a Portuguese hemisphere in the Treaty of Tordesillas of 1494, the re-established graticule gained political importance.
In 1634 a prime meridian was fixed on El Hierro as the westernmost Canary Island by the Faro de Orchilla and it was not until 1884 that the Greenwich meridian, which has been in use in England since 1738, prevailed against other national prime meridians.
The Nouvelle Triangulation de la France , based on the measurements by Jacques Cassini and Jean Dominique Comte de Cassini from the period before 1793, took place in the course of metrification (the conversion of all relevant dimensions to the meter as the standard). The prime meridian runs through Paris, so that the “Old Royal Observatory” in Greenwich in grads is at 2 ° 20 ′ 14.025 ″ W (NTF). This also included the decimal division of the degree in grads, degrees (nouvelle), today legally as gon (1 full angle = 400 grads).
While the Greenwich Meridian has prevailed, the gon angle and the 400 ° division became the geodetic standard in Central Europe. The circular division into 360 ° is often only understood to a limited extent as a terrestrial graduation (graticule) in the sense of metrification.
See also
- History of astronomy
- Coordinate reference system
- Polar coordinates
- Swiss national coordinates
- Orthodrome , Loxodrome
- Georeferencing
- Map network design (map projection for generating maps)
Web links
- Determine longitude and latitude of places and your own position
- Determine and convert geographic coordinates
Individual evidence
- ↑ Claudios Ptolemaios: Geographike Hyphegesis, chap. 10. Germania Magna (compare the degrees with those of today's maps)
- ↑ An alternative route to mapping history ( Memento from July 17, 2012 in the web archive archive.today )