Fractions
In a narrower sense, fraction calculation refers to calculating with common fractions (sometimes also ordinary fractions ) in the "numerator-fraction-denominator notation" (see below). Fractional calculation is part of arithmetic , a branch of mathematics .
In a broader sense, the word is also used for arithmetic with rational numbers , regardless of the way they are written.
A more important extension consists in the admission of fraction terms , which are expressions that are formally formed like common fractions, but in which numerator and denominator can be terms that contain variables . The rules for calculating fractions apply analogously to these fraction terms. Calculating with fraction terms is part of algebra .
The rules of fractions relate to the basic arithmetic operations , i.e. to addition , subtraction , multiplication , division and the formation of reciprocal values . Especially with fraction terms, there are also rules for powers and roots.
There is also a reduction and expansion rule , which are a special feature of fractions. It is based on the difference between a fraction and a fraction , which is explained in more detail in the following section.
Fractional spelling, i.e. the spelling with a fraction line, is used quite generally in various areas of mathematics, especially in algebra , whenever the elementary rules of fractions, in particular the reduction and expansion rule, apply in the structure being examined. Here, too, one speaks of “fractions” whenever these rules are applied.
Fraction and Fractional Number
The fraction calculation is based on the fact that the whole (the one from calculating with natural numbers) can still be subdivided. For example, a cake can be divided into four parts. If these pieces are the same size, each piece is a quarter of the cake. If, as in the picture, one of the quarters is already missing, three quarters of cakes are shown.
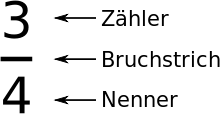
This is usually written in the "numerator-fraction-line-denominator notation": The number under the fraction line - the so-called denominator or divisor - indicates how many parts the whole has been divided into; the number above the fraction line - the numerator - indicates how many parts of it are meant in this case. This is how you get a fraction . This can also be interpreted as follows: The numerator indicates how many whole parts are to be divided into as many equal parts as the denominator indicates. (You place three cakes on top of each other and divide the stack into four equal partial stacks.)
If the whole (the cake) is instead divided into eight parts and six of them are taken, that is a different fraction: instead of . But these two fractions seem to represent the same amount of cake: they represent the same fraction .
For each fraction there are many (infinitely many) different representations , different fractions , all of which represent the same value (the same quantity ), but in different ways. One can get from one fraction to another by expanding and shortening . This does not change the value of a fraction, but you get different ways of representing this number: different fractions.
Definition and terms
Fractions can initially be divided into common fractions (also called ordinary fractions ) and decimal fractions (= decimal number, colloquially: "point number"), and there is also the representation as a mixed fraction. When one speaks of a fraction, one usually means a common fraction, calculating with decimal fractions is usually not called a fraction calculation.
The table below summarizes the common fractions used and explained in this section. The terms in the table below each fall under the generic terms above, for example every pseudo fraction is a common fraction, adjacent terms need not be mutually exclusive. Please note that these are designations for number spellings and not for the numbers shown. A certain number can have different representations, each of which is identified with different terms from the table. For example, you can write every improper fraction as a mixed fraction.
| fracture | ||||||
| common break, common break | mixed fraction | Decimal fraction | ||||
| real break, real break | improper break, improper break | |||||
| Broken trunk | Branch break, derived break | Sham break, improper break |
improper fraction that is not an apparent fraction |
|||
Other forms in which fractions can be displayed ( continued fraction , percentage and per thousand notation , binary fractions , etc.) are dealt with in each separate articles and not included in this table.
Common fractions
Common fractions are generally represented by superimposing the numerator and denominator , separated by a horizontal line:
The numerator and denominator of a fraction are whole numbers . The denominator must not be zero , as division by zero is not defined.
Each fraction can also be understood as a division problem. The numerator is the dividend , the denominator is the divisor:
The decisive factor in fractions is that every division (except by zero) is possible and has a result that can be easily represented, while the rules of divisibility apply to whole numbers .
Normally, natural numbers are used for the numerator and denominator and any negative sign is placed in front of the fraction, for example instead of or . If the numerator and denominator are negative, this denotes the positive fraction according to the rules of division of whole numbers :
In a variant of this notation, which is often used when common fractions occur in texts, the numerator, fraction line and denominator are written one after the other and a slash is used as the fraction line , for example 1/2, 3/8. In the notation slash in place of the horizontal fraction bar are (especially) digit numerator and denominator sometimes reduced over or written under the slash: 6 / 7 . For this purpose, there are special characters in many printing character sets, such as or ½.
Real and spurious fractions
If at a fraction of the amount of the counter is smaller than that of the denominator, then one speaks of a real or actual fracture (z. B. or ), otherwise from a fake or improper fraction (z. B. or ).
So real fractions are those whose amount is smaller than a whole.
Trunk breaks and branch breaks
If the numerator in a common fraction is 1 (e.g. or ), we speak of a trunk fraction , otherwise it is a derived fraction or branch fraction .
Pseudo breaks
Improper fractions, where the numerator is an integer multiple of the denominator (e.g. ), are called dummy fractions because they can be converted into whole numbers by shortening them (in the example to the number 4). In particular, every whole number can be written as a dummy fraction .
Mixed fractions
Improper fractions that are not pseudo-fractions can always be represented as mixed fractions (also: as mixed numbers, in mixed notation).
First of all, the whole number part, i.e. H. the number rounded to zero, written and then immediately afterwards the remaining portion as a real fraction. For example instead of or instead of .
One problem with mixed spelling is that it can be misunderstood as a product:
So mostly stands for and not for .
If you write on the other hand , it is not a fraction in mixed notation, but (because of the variables) a term . Here the omitted arithmetic symbol must be a painting point (other arithmetic symbols must not be omitted in terms). must therefore be understood as and never as .
Calculation rules
Practical arithmetic with fractions
When calculating with fractions in the four basic arithmetic operations of addition , subtraction , multiplication and division , two fractions are linked to create a third number. This must not be confused with reshaping fractions, whereby a single fraction is given a new shape without changing its value.
The forming (the change in shape) is often the prerequisite for fractures to be expected. So it will be dealt with here first.
Change in shape of fractures
Convert to a decimal number
To convert a fraction to a decimal, simply divide the numerator by the denominator. gives 0.75 or 75% of the whole.
Expand and shorten
The value of the fraction represented by a fraction does not change if you multiply the numerator and denominator of the fraction by the same number (not equal to 0) ( expand the fraction ) or divide the fraction by a common factor of the numerator and denominator ( shorten the fraction ).
Example: . Read from left to right the fraction has been expanded, and from right to left shortened.
Set up mixed numbers and split off whole ones
The value of a fraction shown in mixed notation does not change if the integer part is written as a dummy fraction with the denominator of the fraction and the remaining fractions are added. Conversely, with an improper fraction, you can split off the fractions that make up the whole and add the remaining fractions.
Example: . Whole numbers were split off from left to right, and mixed numbers were set up from right to left.
Make fractions with the same name
Common fractions that have the same denominator have the same name . If fractions are expanded in such a way that they then have the same denominator, this is called making the same name . In practical arithmetic, the main denominator of the fractions should be determined, which is the lowest common multiple (lcm) of the denominator.
Example: The fractions should have the same name. The LCM is the denominator , so all three fractions are expanded so that their denominator is 42:
- .
The representations of the same name can now be used, for example, to order the displayed fractions according to size by comparing their counters:
- , so must apply.
The basic arithmetic
Add and subtract
The fractions that are to be added or subtracted are first given the same name, then their counters are added or subtracted.
Example: .
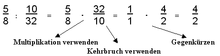
Multiply
Fractions are multiplied by multiplying their numerators and denominators together. The product of the numerator is then the numerator of the result, the product of the denominator is then the denominator of the result.
Example: .
To divide
A fraction is divided by multiplying by its reciprocal .
Example: .
As shown in the example, intermediate results can be shortened (here for example the 3 and 2 in the penultimate step).
Doing math with mixed fractions
When multiplying or dividing mixed fractions, it is usually necessary to first convert them to ordinary fractions. (Except for very simple tasks, such as .)
When adding and subtracting, on the other hand, it is much cheaper to look at the whole thing in isolation and only use fractions for the remaining real fractions. When adding, an additional whole can appear here, when subtracting the fractions may not be sufficient, so that one of the whole has to be split up to form an apparent fraction:
- ;
- .
Abstract rules of calculation
The following rules apply to both fractions in the narrower sense and when calculating with fraction terms. When calculating with fractions, the variables in the rules represent certain whole numbers. If you instead use other expressions for these variables, e.g. If, for example, you enter real fractions, decimal fractions or terms yourself, then you get rules for calculating with fraction terms, fractions in the broader sense.
When calculating with fractions, the abstract calculation rules always provide correct results, and the calculation with the “practical calculation rules” is often less time-consuming.
Expand and shorten
| Shorten |
|---|
| Expand |
Helpful donkey bridges are:
- Cut factors, that's good; whoever cuts sums is a sheep.
- Differences and sums only cut the stupid.
- What you do above, you do below!
From the equivalence for any natural numbers it follows that every rational number can be represented by an infinite number of different fractions, because it holds .
addition
subtraction
multiplication
division
So you divide by a fraction by multiplying by the reciprocal of the fraction, which acts as a divisor . The division is therefore reduced to the multiplication.
Potencies
| rule | example |
|---|---|
Calculating with fraction terms
Fractional terms, i.e. arithmetic expressions in the form of common fractions, play an important role in elementary algebra. Generally fraction Terme also contain numbers next variables . The calculation rules for fractions can also be applied to fraction terms.
Domain of definition
When determining the definition range of a fraction term, it should be noted that the denominator must not have the value 0. For example, the fraction term that depends on would not be defined when inserting . The domain is therefore if the set of real numbers is assumed as the basic set . In more complicated cases, the denominator should be broken down into factors so that the domain of definition can be identified.
Example: has the domain of definition .
Shorten
Shortening means that you divide the numerator and denominator by the same arithmetic expression. It is important that only factors of products can be removed. Sums and differences in the numerator and denominator may first have to be broken down into products ( factorization ).
Examples:
If a fraction term is shortened, the definition range can change! In the first example, the unabridged term on the left is only defined if it applies, the one on the right is already defined if only applies. In the second example, the unabridged term is only defined if the abbreviated term is defined without restrictions.
Changing the definition range of a fraction term when shortening it is one of the techniques with which function terms can be continued continuously .
Addition and subtraction
As with numbers, it is necessary to give the given fraction terms the same name, i.e. H. to bring to the same denominator. The simplest possible common denominator (main denominator) is determined, which is divisible by all given denominators.
Example:
The main denominator is . The expansion factors of the three given fraction terms are obtained by dividing the main denominator found by the previous denominator. So the expansion factors are , and .
Often the main denominator can only be identified if the denominators are broken down into factors (factorization). One often falls back on the method of factoring out or uses binomial formulas .
Example:
Multiplication and division
When multiplying fraction terms, both the numerators and denominators must be multiplied. Common numerator and denominator factors should be truncated.
Example:
In more complicated tasks, the numerator and denominator should be broken down into factors in order to be able to remove them before the actual multiplication.
Example:
The division of fraction terms can be reduced to multiplication. You divide by a fraction term by multiplying by its reciprocal .
Example:
Other forms of representation
Partial fractions
Fractions can often be broken down into so-called partial fractions , the denominators of which are whole powers of prime numbers ; z. B .:
Egyptian fractions
There are also decompositions as so-called Egyptian fractions ( stem fractions ), e.g. B.
- and
- ,
the ancient Egyptians only knew and calculated such sums.
Pythagorean fractions
The number triple is an example of a Pythagorean fraction (see also Pythagorean triple ), because
- .
Rational numerator or denominator
See rationalization (fractions) .
Generalizations
The construction of the field of rational numbers as fractions from the ring of whole numbers is generalized in abstract algebra by the concept of the quotient field to any integrity rings.
See also
literature
- Erhard Cramer, Johanna Nešlehová: preliminary course in mathematics . Workbook for the start of studies in bachelor's degree programs. 3rd, verb. Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-78180-6 , pp. 77–83 (( limited online copy in Google Book Search - USA )).
- Friedhelm Padberg: Common Fractions - Decimal Fractions . Fractional Calculation Didactics. BI-Wissenschafts-Verlag, 1989, ISBN 3-411-03207-3 .
Web links
- Fractional calculation illustrated in tutoring videos (Olaf Hinrichsen, OberPrima.com UG, March 16, 2018)
- Fraction calculator - various online programs for fractions
- Formulas for calculating fractions - A clear list of the most important formulas for calculating with fractions
- Interactive applet that guides you through the various tasks to calculate fractions