Quotient field

In algebra , the quotient field of a ring (with certain properties) is a superset of this ring, onto which the addition and multiplication of the ring are continued and in which every element except one multiplicative inverse has. The most prominent example is the field of rational numbers as the quotient field of the ring of whole numbers . A generalization of the concept for rings that are not necessarily zero divisor is given by the localization . ${\displaystyle 0}$

definition

Let it be a commutative ring that is different from the zero ring and free of zero divisors . The smallest body that can be embedded in is called the quotient body or body of the fractions of the ring. The symbolic abbreviation or is common . ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle \operatorname {Quot} (R)}$ ${\displaystyle \operatorname {Q} (R)}$

Remarks

For the zero ring, the set in the definition below would be empty. The ring must be free of zero divisors, otherwise the multiplication would not be well defined for with (see below). If the ring is not commutative, only an inclined body is created , which is not necessarily a body. ${\displaystyle M}$ ${\displaystyle b,d\in R\setminus \{0\}}$ ${\displaystyle bd=0}$

Each ring of the above kind can be embedded in a "smallest" body, i.e. H. All bodies in which the ring can be embedded contain a partial body that is isomorphic to this smallest body, the quotient body of the ring; in particular, it can thus be also extended to a ring integrity by forming the quotient of the body and to be adjoined. That is, is the smallest integrity ring that contains. ${\displaystyle 1\in \operatorname {Quot} (R)}$ ${\displaystyle R\subset \operatorname {Quot} (R)}$ ${\displaystyle R[1]\subset \operatorname {Quot} (R)}$ ${\displaystyle R}$

In particular, every integrity ring fulfills the required properties; however, an element that the integrity ring also requires is not necessary in order to be able to form the quotient field. However, many authors are calling for an integrity ring to improve clarity.

The construction of the quotient field is a special case of localization .

properties

• The quotient field of a body is the body itself, except for isomorphism.
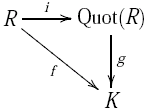
• In abstract terms, the quotient field of a ring is defined by the following universal property : A quotient field is a pair , where a body and an injective ring homomorphism , with the property that for each pair , where a body and an injective ring homomorphism, there is exactly one injective body homomorphism gives with . This clearly means that you can also embed the quotient of in every body in which you can embed (the latter embedding being a continuation of the first). ${\displaystyle R}$ ${\displaystyle (\operatorname {Quot} (R),i)}$ ${\displaystyle \operatorname {Quot} (R)}$ ${\displaystyle i\colon R\to \operatorname {Quot} (R)}$ ${\displaystyle (K,f)}$ ${\displaystyle K}$ ${\displaystyle f\colon R\to K}$ ${\displaystyle g\colon \operatorname {Quot} (R)\to K}$ ${\displaystyle f=g\circ i}$ ${\displaystyle R}$ ${\displaystyle R}$

From the latter property it follows that there is the smallest body that contains, and that this is uniquely determined except for isomorphism, so it is justified to speak of the quotient field. ${\displaystyle \operatorname {Quot} (R)}$ ${\displaystyle R}$

construction

The quotient field of a ring can be constructed as follows: ${\displaystyle (\operatorname {Quot} (R),i)}$ ${\displaystyle R}$

• Explain the equivalence relation ${\displaystyle M:=R\times \left(R\setminus \{0\}\right)}$

${\displaystyle (a,b)\sim (c,d)\quad :\!\!\iff \quad ad=cb}$.

• Usually one writes for the equivalence class of . ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle (a,b)}$
• If one is equal to the set of equivalence classes . ${\displaystyle Q}$ ${\displaystyle Q:=M/{\sim }=\left\{{\tfrac {a}{b}}\mid (a,b)\in M\right\}}$
• Define on addition and multiplication as follows: ${\displaystyle Q}$

${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}\ :=\ {\frac {ad+cb}{bd}},\qquad {\frac {a}{b}}\cdot {\frac {c}{d}}\ :=\ {\frac {ac}{bd}}}$

In particular, the operations defined in this way are well-defined, i.e. the two sides are independent of the choice of representatives.

• The ring is not the null ring, so it contains an element . The neutral element with respect to addition (the zero element) is , the neutral element with respect to multiplication (the one element) is . These equivalence classes are the same for everyone . In the case of the integrity ring, this is usually chosen. ${\displaystyle a\neq 0}$ ${\textstyle {\frac {0}{a}}}$ ${\textstyle {\frac {a}{a}}}$ ${\displaystyle a\in R\setminus \{0\}}$ ${\displaystyle a=1}$
• For the inverse with respect to the addition is given by, and if is, is invertible with respect to the multiplication, where the inverse is given by . ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle {\tfrac {-a}{b}}}$ ${\displaystyle a\neq 0}$ ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle {\tfrac {b}{a}}}$
• Thus, a body, in particular is for an integrity ring , is an injective ring homomorphism which mediates the desired embedding. It applies . ${\displaystyle (Q,+,\cdot )}$ ${\displaystyle i\colon R\to Q}$ ${\displaystyle a\mapsto {\tfrac {a}{1}}}$ ${\displaystyle \operatorname {Quot} (R)=(Q,+,\cdot )}$

For the well-defined structure of , the truncation rule in rings with zero divisors is decisive, i. that is, it always follows for from . ${\displaystyle \operatorname {Quot} (R)}$ ${\displaystyle a\neq 0}$ ${\displaystyle ax=ay}$ ${\displaystyle x=y}$

Examples

• The quotient field of the integrity ring of integers is the field of rational numbers . ${\displaystyle \operatorname {Quot} (\mathbb {Z} )}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Q} }$
• The quotient field of the ring of even integers (a ring without one) is also the field . ${\displaystyle \operatorname {Quot} (2\mathbb {Z} )}$ ${\displaystyle \mathbb {Q} }$
• The quotient field of the polynomial ring is often defined as the rational function field. ${\displaystyle \operatorname {Quot} {\big (}K[X]{\big )}}$ ${\displaystyle \displaystyle K(X)}$
• The quadratic number field is the quotient field of the Gaussian numbers ${\displaystyle \mathbb {Q} (\mathrm {i} )}$ ${\displaystyle \mathbb {Z} [\mathrm {i} ]}$
• Let be the integrity ring of the whole functions and the body of the meromorphic functions. With Weierstraß's product theorem one can see that each can be written on a meromorphic function as a quotient of two whole functions, consequently is . ${\displaystyle {\mathcal {O}}(\mathbb {C} )}$ ${\displaystyle {\mathcal {M}}(\mathbb {C} )}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle {\mathcal {M}}(\mathbb {C} )=\operatorname {Quot} ({\mathcal {O}}(\mathbb {C} ))}$

literature

• Thomas W. Hungerford: Algebra . 5th edition. Springer, 1989, ISBN 0-387-90518-9 .

On applications in function theory :

• Eberhard Freitag, Rolf Busam: Function Theory 1 . 3. Edition. Springer, 2000, ISBN 3-540-67641-4 .