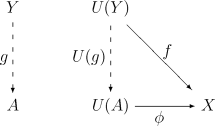Universal property

A universal property is a method of mathematics , and especially abstract algebra , of obtaining a desired structure without specifying a concrete construction. For objects of a certain category , e.g. B. the category of abstract algebras , set a property, e.g. B. that there is an injective mapping into algebra of a vector space . ${\displaystyle \mathbf {C} }$ ${\displaystyle V}$

The universal construction now consists in asserting the existence of a "smallest" element of the category which fulfills the property. In the example this would be the tensor algebra of . To be "smallest" means that there is a clearly defined morphism for each object of the category that fulfills the required property , which is compatible with the property, in the example with the embedding of . ${\displaystyle U}$ ${\displaystyle TV}$ ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle f\colon U\to W}$ ${\displaystyle V}$

The "smallest" element does not have to be uniquely determined, but all "smallest" elements, if they exist, are isomorphic . A concrete construction is usually given as a proof of existence, but mostly the details of the construction are not essential for the theory of the structure.

Examples

• the homomorphism of a group on the factor group according to a normal divisor
• the tensor algebra , see above.
• the core of a linear map.
• the linear hull of a subset of a vector space as the smallest subspace that contains this set.
• the affine hull of a subset of an affine space.
• the convex hull of a subset of an affine space.
• the algebraic closure of a body
• the free termalgebra .
• the topological closure of a subset of a topological space.
• the interior of a subset of a topological space as the largest open set contained in the subset.

motivation

What are universal properties good for? Once you have recognized that a certain construction fulfills a universal property, you gain from this

• Universal properties define objects except for isomorphisms; showing that two objects have the same universal property is thus a possible strategy for showing their isomorphism.
• The exact details of the given construction may be complex and extremely technical in nature, but thanks to the universal property one can forget all these details: everything one needs to know about the construct is already contained in the universal property. If one uses the universal property instead of the concrete details, this usually makes a proof short and elegant.
• If the universal construction can be carried out for every object in a category , we get a functor in the target category. ${\displaystyle X}$ ${\displaystyle \mathbf {C} }$
• This functor is also right or left adjoint to a given functor. But such functors basically exchange with Kolimites or Limites . In this way, it immediately follows, for example, that the kernel of the direct product of two linear mappings is equal to the product of the kernels (is canonically isomorphic).

Formal definition

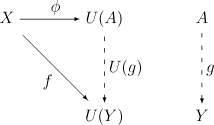
Let be a functor from the category into the category and be an object of . A universal morphism from to consists of a pair , where an -object and a morphism is in, so that the following universal property is satisfied: ${\displaystyle U\colon \mathbf {D} \to \mathbf {C} }$ ${\displaystyle \mathbf {D} }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle X}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle X}$ ${\displaystyle U}$ ${\displaystyle (A,\phi )}$ ${\displaystyle A}$ ${\displaystyle \mathbf {D} }$ ${\displaystyle \phi \colon X\to U(A)}$ ${\displaystyle \mathbf {C} }$

• For every object and every -Morphismus , there is exactly one morphism , so true, i. H. so that the following diagram commutes : ${\displaystyle \mathbf {D} }$ ${\displaystyle Y}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle f\colon X\to U(Y)}$ ${\displaystyle g\colon A\to Y}$ ${\displaystyle f=U(g)\circ \phi }$

Intuitively, the existence of means that "is general enough", while uniqueness ensures that it is not "too general". One can also reverse all arrows in this definition, i.e. H. consider the category-theoretical dual . A universal morphism from to is a pair , where an -object and a morphism is in, such that the following universal property is satisfied: ${\displaystyle g}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle U}$ ${\displaystyle X}$ ${\displaystyle (A,\phi )}$ ${\displaystyle A}$ ${\displaystyle \mathbf {D} }$ ${\displaystyle \phi \colon U(A)\to X}$ ${\displaystyle \mathbf {C} }$

• For every object and every -Morphismus , there is exactly one morphism , so true, i. H. so that the following diagram commutes: ${\displaystyle \mathbf {D} }$ ${\displaystyle Y}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle f\colon U(Y)\to X}$ ${\displaystyle g\colon Y\to A}$ ${\displaystyle f=\phi \circ U(g)}$

properties

Existence and uniqueness

The mere definition does not guarantee existence. A universal morphism from to may or may not exist for a functor and an object as above . If, however, a universal morphism exists, it is unambiguous except for unambiguous isomorphism. If there is another such pair, there is a clear isomorphism with . This can easily be seen by applying the definition of the universal property to . ${\displaystyle U}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle U}$ ${\displaystyle (A,\phi )}$ ${\displaystyle (A',\phi ')}$ ${\displaystyle g\colon A\to A'}$ ${\displaystyle \phi '=U(g)\circ \phi }$ ${\displaystyle (Y,f)=(A',\phi ')}$

Equivalent formulations

The definition of a universal morphism can be formulated in different ways. With a functor and an object , the following statements are equivalent: ${\displaystyle U\colon \mathbf {D} \to \mathbf {C} }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle X}$

• ${\displaystyle (A,\phi )}$is a universal morphism from to ${\displaystyle X}$ ${\displaystyle U}$
• ${\displaystyle (A,\phi )}$is an initial object of the comma category ${\displaystyle (X\downarrow U)}$
• ${\displaystyle (A,\phi )}$is a representation of the functor ${\displaystyle \operatorname {Hom} _{\mathbf {C} }(X,U({-}))}$

Accordingly, the dual statements are equivalent:

• ${\displaystyle (A,\phi )}$is a universal morphism from to ${\displaystyle U}$ ${\displaystyle X}$
• ${\displaystyle (A,\phi )}$is an end object of the comma category ${\displaystyle (U\downarrow X)}$
• ${\displaystyle (A,\phi )}$ is a representation of the functor ${\displaystyle \operatorname {Hom} _{\mathbf {C} }(U({-}),X)}$

Relationship to adjoint functors

Be a universal morphism from to and one from to . Because of the universal property exists for each morphism exactly one morphism with . ${\displaystyle (A_{1},\phi _{1})}$ ${\displaystyle X_{1}}$ ${\displaystyle U}$ ${\displaystyle (A_{2},\phi _{2})}$ ${\displaystyle X_{2}}$ ${\displaystyle U}$ ${\displaystyle h\colon X_{1}\to X_{2}}$ ${\displaystyle g\colon U(X_{1})\to U(X_{2})}$ ${\displaystyle U(g)\circ \phi _{1}=\phi _{2}\circ h}$

Is there even any object category universal morphism for so defines the mapping , a functor . The morphisms reproduce a natural transformation of (the identity function on ) . Then there are a pair of adjoint functors , left-adjoint to and right-adjoint to . ${\displaystyle X_{i}}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle U}$ ${\displaystyle X_{i}\mapsto A_{i}}$ ${\displaystyle h\mapsto g}$ ${\displaystyle V\colon C\to D}$ ${\displaystyle \phi _{i}}$ ${\displaystyle 1_{\mathbf {C} }}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle U\circ V}$ ${\displaystyle (V,U)}$ ${\displaystyle V}$ ${\displaystyle U}$ ${\displaystyle U}$ ${\displaystyle V}$

The same applies mutatis mutandis in the dual case.

history

Universal properties were introduced in connection with various topological constructions by Pierre Samuel in 1948 . Nicolas Bourbaki later used it extensively. The closely related concept of adjointness of functors was introduced independently by Daniel Kan in 1958.

See also

• Free group
• Monad