Division (math)
The Division is one of the four basic arithmetic operations of arithmetic . It is the reverse of multiplication . The division is also known colloquially as dividing . A dividend is divided by a divisor, the result is called the quotient. The long division is the method of sharing with pen and paper. It is taught in primary school lessons. The arithmetic symbol for the division is , or (divided symbol ).
definition
In order to be able to discuss division as the well-known basic arithmetic calculation, one needs a mathematical structure that knows two links (arithmetic operations), called addition and multiplication. The two links interact with each other according to the rules of the mathematical ring . The multiplication defines the division as the associated reverse operation. Addition is required as an additional basic arithmetic operation because it defines, for example, zero (0) as the neutral element belonging to it .
- comment
- In the known from school mathematical structures of the integers of the rational numbers of real numbers and the complex numbers is mathematical rings.
Parts or dividing means to a given number (the known factor of) an appropriate number (the unknown factor) to find, so that the multiplication of a desired product gives: find, for a given and one such that .
If you limit yourself to whole numbers , this is not always possible (see divisibility ).
In bodies , for example in the body of rational numbers or in the bodies of real numbers and complex numbers , the following applies:
- For every number and for every non-zero number, there is exactly one number that satisfies the equation .
The division is therefore the reverse of the multiplication to determine this . One writes
" (Read:" equally divided by "or in short" equal by "or also" equally divided by ")."
The following mean:
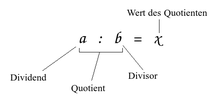
- The number that is divided, “dividend” ( Latin for “the one to be divided” (namely: number)), in fractions also “numerator” .
- The number by which one divides , "divisor" or "divisor" ( Latin for 'the one who divides'), also called denominator in fractions .
- The term is called " quotient ".
- The result of the division is called the "value of the quotient" or quotient value , often also quotient for short .
Memory aids:
- Dividend by divisor equals the value of the quotient.
- Dividend: Divisor = value of the quotient ( donkey bridge : dividend comes before divisor in the alphabet )
properties
Neither the commutative law nor the associative law applies to division . However, it can be traced back to multiplication because it holds
- .
It can therefore be advantageous to write the division as a multiplication with the reciprocal value , since the multiplication is both associative and commutative and thus allows easier and less error-prone reshaping. For the division, however, the second distributive law applies with addition and subtraction , that is
- and .
One speaks here of the legal distributivity of the division. However, the first distributive law (left distributivity) is generally not satisfied with addition and subtraction.
If there are several successive divisions in one line, the order is processed from left to right; the division is therefore left-associative :
- .
Arithmetic division by zero is not possible
example
Example from a pastry shop: If you want to split a cake between zero people, how much of the cake does each person get?
It is not possible to answer the question as there is no one to get the cake. If you translate this question into the language of mathematics and abstract from all possible extra-mathematical meanings, the clear question “How do I distribute something to 0 places?” Becomes the purely mathematical problem “How do I divide by 0?”.
Mathematical proof
Let be a ring with zero element . With "Division by zero" the known factor (divisor) is asked:
- Is there a solution to the equation for an element
If the zero ring , i.e. consists of the only element 0, then the equation has the solution because it is because there is nothing else, and thus as required. Moreover, is the only solution.
In the following, it is generally assumed that it has at least 2 different elements, which is the case, for example, with a body by definition .
Find solutions to the equation for a ring element .
- Case 1: :
- For a ring member , the equation is not solvable , not in and not in an extension ring . Because, as shown in the article Ring (Algebra) , it follows from the ring axioms , essentially the distributive law :
- The neutral element of the addition of a ring is an
- Case 2: :
- Although the above equation has a solution in the case of each ring element , specifying a particular one of them (“making the division unique”) would lead to problems. When settling, for example, you choose a ring element . (This is possible because it has at least 2 elements.) The associative law of multiplication would result in:
- ,
- which would contradict the choice .
As a result, this means that quantities which, when they are added and multiplied , know a “division by zero” in any form ( infinite , undefined , NaN or whatever ) cannot be rings (let alone bodies) because the ring properties cannot for the quotients with divisor zero - and therefore not valid for all elements .
- Remarks
- If the ring has zero divisors , such as B. the ring of the remainder classes modulo 6 the remainders , then
- the equation cannot be solved for every one . Example: has no solution in because it does not contain the rest .
- can have an equation with multiple solutions. Example: has the three solutions .
- the equation cannot be solved for every one . Example: has no solution in because it does not contain the rest .
- In the scientific mathematical literature, division by zero is only mentioned if this is the subject of the chapter.
Division by zero in the computer
Especially when you spontaneously use a computing device, it can happen that you divide by zero . The goal of the implementations is then
- to make the user / programmer aware of the event and
- to deliver an (interim) result with which the most promising further calculation can be expected.
Fixed point
A division by zero with fixed point numbers triggers a runtime error (an exception) of the division by zero type ( zero-divide exception ) on practically all electronic computing systems . An associated handling of this exception is usually specified and performed by the runtime environment of the programming language used, but can also be specified in more detail by the user, for example by means of an instruction. In some runtime environments, division by zero will cause undefined behavior .
catch
Since the kernel (in cooperation with the runtime environment of the programming language) provides the error-handling runtime environment, a division by zero in the kernel itself can cause the entire computer to crash .
Floating point
If an "overflow" occurs during a floating point operation , i. H. the result is too large in terms of amount to be displayed if it is set to a very large floating point number with the meaning "infinite". A floating point division by zero is also often treated in this way. B. from the very popular IEEE 754 standard . A flag is also set so that exception handling can be programmed. (The article Permanence Principle discusses various concepts of how a “division by zero” could be defined with the least possible waiver of calculation rules, e.g. ring axioms and order relations.)
Is 1: 0 = ∞?
Some people believe that the solution of dividing by zero must be infinite , since experience shows that the individual gets more and more the fewer there are with whom he has to share something. But
- firstly, by introducing a "value", the ring structure and its arithmetic - as shown above - are abandoned. More far-reaching consequences are the indefinite expressions that now appear (to which the expressions of the type actually already belong and) all of which require special treatment.
-
Secondly, a new mathematical concept (going beyond arithmetic, namely a topological ) comes into play through the method of limit value formation , with which in some cases a meaningful result can be determined for a task that cannot be directly calculated. However, if you apply this method to the example , the result actually strives towards infinity, but only if you approach zero from the positive side, i.e. if you approach zero from the direction of the negative numbers, then the Value of the function against , so the function at the point strives against as well as against , so it has no clear limit value. As the example shows, there are additional problems relating to the structure and the important order relation. If you absolutely always want to assign a value to division (including division by zero), then this must also have the uniqueness that is otherwise usual for division; a determination of such a value is unsatisfactory for every choice, and the assignment of a solution set is also unsatisfactory .
- Résumé
- The complications that go hand in hand with the introduction of a “value” for are in every respect (in particular the restriction of the validity of the arithmetic, the resulting inflation of the necessary calculation rules, ambiguity) much more disadvantageous than the simple acknowledgment of the simple fact that equations of the type have no solution. Rather, there are many new problems that cannot be properly treated with such a calculation.
- Depending on the given case it is often possible, with methods of analysis of additional with the addition of information, for example. Monotony and continuity to come to a sound solution, a solution that remembers only completely removed to a "divide by zero".
Division with remainder
In the area of whole numbers, the following applies: A division can only be fully carried out if the dividend is an integral multiple of the divisor. In general, however, the division is not completely feasible, that is, there is a remainder.
Spellings
There are several ways of writing the division: or or or
The colon as a symbol for division has only been common practice since Leibniz (1646–1716), although it is also known in older writings. William Oughtred introduced the notation in his Clavis Mathematicae of 1631.
The notation is also called fraction representation or fraction for short . Fractional notation is only unique for commutative multiplication; this plays a role in more general mathematical structures, as mentioned below under “Generalization”.
generalization
In abstract algebra defining algebraic structures , the body are called. Bodies are characterized by the fact that division (except by 0) is always possible in them. The division takes place here by multiplication with the inverse element of the divisor.
In more general structures (with non-commutative multiplication) a distinction has to be made between left division and right division. The (non) validity of the associative law also has an influence on the properties of quotients.
Country-specific
In Austria, a distinction is occasionally made between trade fairs (how often does it go in ...?) And parts (how much does it result in divided by ...?).
Until the 1970s, a distinction was occasionally made between dividing (in groups) (Austrian fairs ) and distributing in German primary schools .
See also
- Group theory
- Ring theory
- Oblique body
- Division algebra
- Polynomial division
- Rational function - division of functions
- Vedic Mathematics - Simplified Method of Dividing
- Quasi-group
- Indefinite expression (mathematics)
literature
- SA Stepanov: Division . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
Web links
Individual evidence
- ↑ It is preferable to the notation with a fraction line, especially in the non-commutative case , because it specifies a clear sequence of operations.
- ^ Rochester Institute of Technology : Order of operations
- ^ Education Place: The Order of Operations
- ↑ Khan Academy : The Order of Operations ( Video, from 05:40 am )
- ^ Virginia Department of Education : Using Order of Operations and Exploring Properties , paragraph 9
- ↑ Chemnitz University of Technology : Precedence rules and associativity
- ↑ "Not solvable" is a sharper statement than "undefined". With the latter, there could still be a degree of freedom for a definition. With the former, this possibility is excluded.
- ↑ A real limit value formation , for example in the manner of de l'Hospital's rule , is not to be regarded as division by zero.
- ↑ a b The article Extended real number brings two topological extensions of the real numbers, but also deals with arithmetic problems.
- ^ Sunk by Windows NT . In: Wired News , July 24, 1998.
- ↑ Python Errors and Exceptions. Retrieved May 30, 2017 (English).
- ↑ Java ArithmeticException. Retrieved May 30, 2017 (English).
- ↑ ISO / IEC 9899: 201x. (PDF; 1.6 MB) Retrieved May 30, 2017 (English, non-normative working document).
- ^ Eric Weisstein , Wolfram MathWorld : Division by zero
- ↑ veritas.at