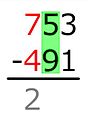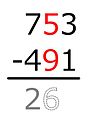subtraction
The subtraction (of lat. Subtrahere "pull", "remove"), colloquially minus calculation called, is one of the four basic arithmetic operations of arithmetic . Under the subtraction means the removal of a number by another. Mathematically , the subtraction is a two-digit combination . The subtraction is the reverse of the addition . The arithmetic symbol for the subtraction is the minus sign "-".
Language regulations, basic properties and notation
The following symbols and ways of speaking are used for the elements of a subtraction:
- The arithmetic symbol for the subtraction is the minus sign "-". It was introduced by Johannes Widmann in 1489 .
- The number from which something is deducted is called minuend (Latin for "the one to be reduced").
- The number that is deducted is called the subtrahend (Latin for "the one to be deducted").
- The arithmetic expression ( term ) that includes the minuend, the minus sign and the subtrahend is called difference .
- The result of a subtraction is the value of the difference (also difference value or just difference ).
- The symbol for differences as terms is the Greek capital letter delta "Δ", which is also used as an operator for difference formation (see below). Often the difference - especially in everyday usage - is only the result of this "minus calculation", and more often the amount of this result. Example: The difference between 7 and 9 and the difference between 5 and 3 is 2 . In the example this is emphasized by the verb “amounts”.
Memory aids (taking into account the sign!):
- Minuend minus subtrahend equals the value of the difference.
- Value of the difference = minuend - subtrahend or
- Minuend - Subtrahend = value of the difference
- ( Eselsbrücke : M inuend comes before S ubtrahend in the alphabet )
Examples (taking into account the sign!):
- 4 minus 1 is written (the same) 3 or differently .
- 4 is the minuend, 1 is the subtrahend, the arithmetic expression (term) is the difference and the result 3 is the value of the difference or the difference value.
The set of natural numbers is not complete with regard to subtraction , that is, with subtraction one possibly achieves a result that exceeds the range of natural numbers .
- Example:
A notation for is what is mainly used in the sense of space-saving application provided the expression is long for .
If several subtractions occur one after the other, the expression is processed from left to right; the subtraction is therefore left-associative :
- .
Mathematical definition
The subtraction is the reverse of the addition . In groups can be given any and exactly one place, so that:
The determination of is called subtraction . can be determined by subtracting ("deducting") from:
is called the minuend , the subtrahend . The result of a subtraction, here , is called the value of the difference . A subtraction is noted with the minus sign:
The subtraction can also be defined as adding the opposite number of the subtrahend to the minuend :
Basic procedure
Graphic method
In the graphic method, the numerical values are represented as bars, lines, points or other abstract objects. Another possibility is the representation with vectors , whereby the direction of the subtrahend vector is reversed and the vectors are then added up.
- example
| • | • | • | • | • | • | • | • | • | • | • | • | • | (13) | |
| - | • | • | • | • | • | • | • | • | • | (9) | ||||
| = | • | • | • | • | (4) |
Subtraction-subtraction method
With the subtraction-subtraction method , part of the subtrahend is deducted from the subtrahend and minuend until the subtrahend is 0. A tens is usually chosen as an intermediate step.
- example
Subtraction-addition method
With the subtraction-addition method , the subtrahend and the minuend are broken down into sub-components, subtracted from these, and then the sub-amounts are added again.
- example
Complement method
With the complement method , the corresponding complement is calculated from the subtrahend . Then the minuend and the complement of the subtrahend are added. The method is especially in the technical computer science , as in the mechanical field Tarrant- Comptometer , the mechanical Hoffritz adder , and electronic adders in modern computer systems may be employed.
- example
Starting formula:
This matches with:
Calculation of the complement:
| surgery | Result value | |
|---|---|---|
| Tens complement | Two's complement | |
| Baseline | ||
| Inversion | ||
| With | ||
Addition:
Written subtraction
In addition to written addition, written subtraction is one of the basic cultural techniques that is learned in the first years of primary school. Mastering the written subtraction is a prerequisite for learning the written division .
Vertical subtraction with carries over
In primary schools today, procedures are mostly taught in which the corresponding positions of the minuend and subtrahend are on top of each other. The positions are processed one after the other, mostly from right to left.
For written subtraction, the minuend (number above) must be greater than or equal to the subtrahend (number (s) below). Negative results are therefore not possible directly.
If the minuend is smaller than the subtrahend, then the signs can be exchanged for the calculation. The subtrahend becomes the minuend (written above) and the minuend becomes the subtrahend (written below). The procedure described below can then be used for calculation. At the end, however, the result must be provided with a minus, because it is always negative (not a natural number). This reverses the change in sign that was previously carried out for the calculation.
If the digit of the subtrahend are larger than the same places the minuend need transfers are handled. That is, the minuend is increased by 10 to enable the subtraction; To compensate for this, either the minuend must be decreased in the column on the left (unbundling process; advance calculation of the transfers) or the subtrahend must be increased (supplementary process; subtraction from right to left). In the German-speaking area, the latter approach has become established with the supplementary procedure. In 2000, a new curriculum came into force in some federal states , which now prescribes unbundling as the standard instead of supplementing it.
Supplementary procedure
With the supplementary method , which is also called the filling technique or (in the USA) the Austrian method ("Austrian method"), no subtraction is made, but the subtrahend is increased up to the end of the minute . If this is not possible, the minuend is increased by 10. The 10 is not “borrowed”, but added as a 1 to the subtract of the next partial calculation. In German-speaking countries, this procedure is taught as a standard method in primary schools. One of the advantages of the method is that it prepares the handling of tasks in which several subtrahends are to be deducted from a minuend.
- example
| description | |
|---|---|
| 1 +… = 3 | |
| The result is written under the line. | |
| 9 +… = 5 The targeted sum (5) is too small! |
|
| It is therefore increased by 10. The 1 is written under the next subtrahend. | |
| 9 +… = 15 The calculation can now be carried out, the result is written under the line. |
|
| (4 + 1) +… = 7 | |
| The result is written under the line. | |
| The overall result. |
Subtraction from left to right
The subtraction can also be carried out from left to right. In this unusual procedure, which is a variant of the supplementary procedure, the transfers are processed before the difference is precisely calculated. Since the transfers neither have to be noted nor memorized, the method is not only relatively resistant to careless mistakes, but also very fast and even suitable for mental arithmetic.
- example
If there is a column or a sequence of several columns in which there are two identical digits, and to the right of it a column with a minuend that is smaller than the subtrahend, the routine “look-ahead” used in this procedure does not only have to have the same two digits but also include the following columns. Each column with the same digits then receives a nine instead of a zero as a result.
The forecast over several columns in the cases described above is a weak point of this method.
Unbundling procedure
Withdrawal with “unbundling” means that the too small Minuend makes a “loan” with his left neighbor. The minuend is increased by 10 and the left neighbor is decreased by 1. The process is used in primary schools, for example. B. taught in the United States as the standard practice. The pure computing effort is similar to that of the supplementary procedure; however, if a zero has to be “borrowed”, it must “borrow” from its own left neighbor - a technique that has to be learned in addition (it is not needed in the supplementary procedure). Also, more needs to be written when unbundling.
- example
| description | |
|---|---|
| 3 - 1 = ... | |
| The result is written under the line. | |
| 5 - 9 =… The minuend (5) is too small! |
|
| It is therefore increased by 10. This 10 is “borrowed” from the number (7) on the left; this is decreased by 1. | |
| 15 - 9 =… The subtraction can now be carried out. The result is written under the line. |
|
| 6 - 4 = ... | |
| The result is written under the line. | |
| The overall result. |
Pre-unbundling
A variant of the unbundling process is that all points are completely unbundled in a first step so that sufficiently large minuends are available for the second step, in which only subtraction is made.
- example
| description | |
|---|---|
| 3 - 1 = possible. No need to “borrow” the number to the left. |
|
| 5 - 9 = not possible. The 5 is increased by 10. Since the 10 is “borrowed” from the 7 adjacent to the left, it must be decreased by 1. |
|
| Processing of the digits: 3 - 1 = 2 |
|
| 15 - 9 = 6 | |
| 6 - 4 = 2 |
Vertical subtraction with no carry-overs
Partial differences
The Partial Differences method differs from other vertical subtraction methods in that it does not use carries over. They are replaced by partial differences, which - depending on whether the minuend or the subtrahend is larger in a column - are given a plus or a minus sign. The sum of the partial differences gives the total difference.
- example
| description | |
|---|---|
| The smaller number is subtracted from the larger: 700 - 400 = 300 Because the minuend is greater than the subtrahend, the difference is given a plus sign. |
|
| The smaller number is subtracted from the larger: 90 - 50 = 40 Because the subtrahend is greater than the minuend, the difference is given a minus sign. |
|
| The smaller number is subtracted from the larger: 3 - 1 = 2 Because the minuend is greater than the subtrahend, the difference is given a plus sign. |
|
| + 300 - 40 + 2 = 262 |
Non-vertical procedures
Exaggeration of the difference
A difference does not have to be calculated digit by digit. Mostly cumbersome, but it is also possible to walk through the number range between a subtrahend and a minuend.
- example
1234 - 567 = can be calculated using the following steps:
- 567 + 3 = 570
- 570 + 30 = 600
- 600 + 400 = 1000
- 1000 + 234 = 1234
To determine the difference, the values of the individual steps are added: 3 + 30 + 400 + 234 = 667.
Decomposition of the subtrahend
Another approach, which is equally suitable for written subtraction as for mental arithmetic, is the breaking up of the subtrahend, which is subtracted from the minuend in individual steps.
- example
"1234 - 567 =" can be calculated using the following steps:
- 1234 - 500 = 734
- 734 - 60 = 674
- 674 - 7 = 667
Same change
The same change subtraction is based on the observation that a subtraction is easy to carry out if there are one or more zeros at the end of the subtrahend. In this process, the subtrahend is therefore increased or decreased to the nearest ten; since the minuend is increased or decreased by the same difference, the manipulation does not affect the difference. If the task is still too difficult after that, the operation can be repeated.
- example
"1234 - 567 =" can be calculated using the following steps:
- 1234-567 = 1237-570 = 1267-600 = 667
Web links
- Examples for stripping with unbundling and extension technology (PDF file; 39 kB)
- Apples - Freeware exercise program for written subtraction
Individual evidence
- ^ Rochester Institute of Technology : Order of operations
- ^ Education Place: The Order of Operations
- ↑ Khan Academy : The Order of Operations ( Video, from 05:40 am )
- ^ Virginia Department of Education : Using Order of Operations and Exploring Properties , paragraph 9
- ↑ Chemnitz University of Technology : Precedence rules and associativity
- ^ Donald E. Knuth: The Art of Computer Programming, Volume 2: Seminumerical Algorithms . 3. Edition. Addison-Wesley, New York 1997, ISBN 978-0-201-89684-8 .
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Trade First
- ↑ Partial-Differences Subtraction ( Memento of the original from June 23, 2014 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. ; The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Partial Differences
- ↑ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Counting Up
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Left to Right Subtraction
- ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Same Change Rule