Adder

The adder (also Addiernetz ) is the main component of the arithmetic unit of a CPU .
The adder enables the addition of two multi-digit binary numbers . Since all four basic arithmetic operations can be traced back to the addition , it forms the central element of the arithmetic unit (arithmetic-logical unit, ALU) of a processor. While the adding network works asynchronously, the adding unit works clocked and buffers the result with memory modules.
An adder can be implemented in different ways. The best-known circuits are the parallel adder, the series adder and the Von Neumann adder. All three use half and / or full adders to perform the addition.
Circuit types
Parallel adder
In its basic form, the carry-ripple adder is used as an adding network, the carry-out being connected to the carry-in of the next full adder. In the worst case, the carry bit signal must migrate from the least significant adder to the most significant adder to form the sum . In large arithmetic units, this results in a considerable runtime in the adding network, and as a result, switching networks with reduced runtime were developed.
- Parallel adder with carry redirection ( carry-skip adder ), the full adder are combined to form groups, and by the addition logic is determined quickly whether a carry-in wanders through the group. (With all adders there is at least a 1 at one input, so all individual adders have a carry in the result.)
- Parallel adders with carry pre- calculation ( carry-look-ahead adder ), the switching network for an adder group contains a complex logic that determines its carry directly.
- Conditional sum adder , calculates the result for an adder group both with and without carry-in set. A selection logic switches the corresponding result to the outputs depending on the carry-in.
The advantage of the parallel adder is that all the adders involved work simultaneously. The disadvantage of the basic form is the long signal delay times, since in extreme cases the transfer has to propagate through the circuit from right to left. The further developments require a large number of additional gates, the number of which increases linearly with the width n of the digits of the dual system to be added .
Series adder
The series adder requires a full adder and a D flip-flop for adding two n -digit binary numbers. In each cycle, the rightmost bit of the binary numbers from the shift registers and the value in the D flip-flop are transferred to the full adder. The result is stored in a register and the carry stored in the D flip-flop for the next clock. The advantage of the series adder is the small number of electronic components required. The disadvantage lies in the serial processing, so that n + 1 clocks are required to add two n -digit binary numbers.
The combination of the advantages of the parallel and series adder leads to the Von Neumann adder.
Von Neumann adding unit
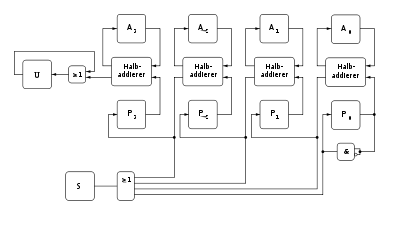
The Von Neumann adder requires n half adders to add two n -digit binary numbers. The addition is done by the following algorithm
Repeat
- Load registers A and P with summands
- Add
- Load register A with sums without carry-over, load carry-over into P
- Repeat actions 2 and 3 until register S contains the value zero
The AND at P 0 ensures that P 0 is set to 0 from then on after the first addition pass .
In the worst case, the adder requires n + 1 clocks; practical experience shows that on average it is only .
Example 13 + 11:
| step | S. | U | P 3… 0 | A 3… 0 | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0000 b | 0 | 0000 b | ||
| 1 | 1 | 0 | 1101 b | 13 | 1011 b | 11 |
| 2 | 1 | 1 | 0010 b | 2 | 0110 b | 22nd |
| 3 | 1 | 1 | 0100 b | 4th | 0100 b | 20th |
| 4th | 1 | 1 | 1000 b | 8th | 0000 b | 16 |
| 5 | 0 | 1 | 0000 b | 0 | 1000 b | 24 |
Subtract
The subtraction is closely related to the addition and can be converted into an addition by changing the sign of the subtrahend. A sign change in binary numbers enables the two's complement , converted as one's complement (inverting all bits) and then added with 1 (setting carry in). The extension of the adding unit to the adding / subtracting unit enables XOR operations to be connected at the input of the second operand . If the selector switch is set to 1, the XOR inverts the input signal and sets the carry-in bit, which creates the two's complement and the addition becomes a subtraction.
Addition and subtraction of floating point numbers
Many processors have a floating point unit for calculations using point numbers. With floating point numbers , the mantissa and exponent are processed separately. For this purpose, the exponents of the numbers are adjusted in a normalizer, the numbers are added with the help of an adder / subtracter and finally the result and the new exponent are processed in a normalizer to form a new floating point number - the result.
Standardizer, part 1
First the exponent has to be adjusted. To do this, the two exponents are subtracted and the mantissa of the floating point number with the smaller exponent is shifted with a shift register by the number of places (bits) determined by subtracting the exponents. This means that both numbers have the same (larger) exponent. The larger exponent is selected via a multiplexer based on the sign of the value resulting from the subtraction (exponent difference) and forwarded directly to the standardizer.
Adder / subtracter
In the adder / subtracter stage, an adder essentially works with upstream inverters at the inputs. The inverters invert (negate) the mantissa if the associated sign bit of the respective floating point number is set. Then the two numbers can be added. This creates the new mantissa. In addition, the priority bit (overflow bit) of the adder is set if the sum of the two mantissas is too large to be able to be saved in the new mantissa.
Standardizer, part 2
In the normalizer, the exponent difference is reduced by one and the result from the adder / subtracter stage is shifted to the left by one if the priority bit is set. The result from the adder / subtracter stage then becomes the mantissa - and the exponent difference becomes the exponent - the result floating point number.
Web links
- Development of a circuit for addition and subtraction of binary numbers ( Memento from September 27, 2007 in the Internet Archive ) - Technical work (PDF file; 952 kB)
- Switching algebra, Boolean algebra