Power (math)
A power (from the Latin potentia 'ability, power' ) is the result of raising to the power ( exponentiation ), which, like multiplication, is an abbreviated notation for repeated mathematical arithmetic operations . As when multiplying a summand is repeatedly added to itself , so when raising a factor is repeatedly multiplied by itself . The number to be multiplied is called the base. How often this base occurs as a factor is indicated by the exponent . One writes:
definition
One speaks as a to the power of n , the nth power of a , a to the nth power or, in short, a to the nth . In this case , a (to) the square is also common.
is called the base (or basic number ), is called the exponent (or high number) of the power . The result is called the power or value of the power.
The definition sets both on the exponent side and on the base side are expanded step by step in the following.
Natural exponents
The potency is for real or complex numbers (common elements of an arbitrary multiplicative monoid ) and natural numbers by
Are defined. This definition only applies to So that the identity that follows from it (also only for ) also applies to, is defined. ( See below for comments on the case .)


The following modification facilitates the handling of the special case :
The power notation means "multiply the number 1 by the base number as often as the exponent indicates", ie
The exponent 0 says that the number 1 is never multiplied by the base number and remains on its own, so that the result is 1.
With a negative base and an even exponent, the power is positive:
With a negative base and an odd exponent, the power is negative:
Whole negative exponents
Negative exponents mean that the operation ( division ) that is inverse to multiplication should be carried out. So "Divide the number 1 by the base number as often as the amount of the exponent indicates".
For a real number and a natural number one defines:
The analogous definition is also used in a more general context whenever multiplication and inverse elements are available, for example with invertible matrices .
Rational exponents
Let be a rational number with the fraction representation with . For any positive real one defines:
- (or, which is equivalent, )
For example:
The value of the power does not depend on which fraction representation you have chosen.
The same definition applies to . It follows that for holds and that for does not exist.
If one allows roots of negative numbers with odd root exponents, then one can extend this definition to negative bases and those rational exponents whose abbreviated fractions have odd denominators . This also includes powers with negative bases and whole exponents, because the denominators are the same in this case .
In this case , all fractions with odd numbers can be used in calculations . However , errors can occur when using fractions with straight lines . For example:
Real exponents
If , is any real number and a sequence of rational numbers that converges to, then one defines:
This definition is correct; that is, the limit value always exists and does not depend on the selection of the sequence .
For example is equal to the limit of the sequence
The definition cannot be extended to the case where in this case the limit value does not need to exist or different limit values result for different choices of the sequence .
Another definition is possible using the natural exponential function and the natural logarithm :
For this purpose, the exponential function can be defined via its series expansion :
Overall, the powers with non-negative bases are thus defined for all real exponents. In contrast, the powers with negative bases are only defined for those rational exponents whose abbreviated fractions have odd denominators. All potencies with negative bases and whole exponents belong to it. Powers of negative numbers with other real exponents can be defined in the area of complex numbers , but they are not real-valued.
Technical spellings
If superscript writing is not possible (for example in an ASCII text), the notation is often used a^b(for example in Algol 60 , in TeX source code or in computer algebra systems such as Maple ), occasionally also a**b(for example in Fortran , Perl or Python ). Because of the various options for defining areas of base and exponent represents Haskell three power operators are available: a^b, a^^band a**b.
Powers of ten are often represented with e or E in electronic data processing or in the display on pocket calculators .
Frequently encountered representation for z. B. −299792458 = −2.99792458 · 10 8
-2.9979 08
|
(8-digit 7-segment display) |
-2.997925 08
|
(10-digit 7-segment display) |
-2.9979256 08
|
(8-digit 7-segment display + exponent field) |
-2.99792458 E+08
|
(16-digit dot matrix display) |
-2.99792458E+08
|
(Floating point representation according to IEEE ) |
Power laws
In order not to overload the following table, we only consider powers with real bases that are not equal . But if you consider one of the laws listed below with only positive exponents, then it is also valid for powers of the base . When speaking of rational numbers with even or odd denominators , the denominators of their abbreviated fractions are always meant.
| for everyone ( see below for comments on "zero to the power of zero" ) | |
| for any real , if is; for arbitrary rational ones with odd denominators, if is. |
|
| for any natural and integer if is; for any natural odd and whole if is.
|
|
| for any real , if is; for arbitrary rational ones with odd denominators, if is.
|
|
| for any real , if is; for arbitrary rational ones with odd denominators, if is.
|
|
| for any natural , and for whole , if ; for any real , if are;
for any rational ones with odd denominators, if at least one of the numbers is negative.
|
|
| for any and whole and, if , also ; for any real , if are;
for any rational ones with odd denominators, if at least one of the numbers is negative.
|
|
| for any whole if is; for any real , if is; for any rational , with odd denominators, if is.
|
If at least one of the exponents is irrational or both are rational, but has at least one of the numbers or an even denominator, then one of the expressions or is for undefined. Otherwise both are defined and either agree or differ only in terms of their sign . For any , if is, and for whole , if is, they always match. These two cases are possible for and not integer but rational . Which case occurs depends on the number of twos in the prime decomposition of the numerator of and the denominator of . In order to recognize the correct sign on the right side of the formula , it is sufficient to insert it into this formula . The sign with which it is then valid remains correct for all and given . Holds for , then holds for all (and also for , if all exponents are positive).
For example, and . Therefore is valid for all and thus for all real ones.
The exponentiation is neither commutative , because, for example, holds , nor associative , because, for example, holds .
The spelling without brackets means that the exponentiation is right-associative, cf. Operator precedence .
Powers of complex numbers
For integer exponents one can define powers with complex bases as in the real case. However, you have to proceed differently for any real or complex exponent.
The first step in defining powers with complex bases and exponents is to continuously extend the function to the set of complex numbers. There are different ways of doing this. For example you can take the number
which converges for all and specifies the function for all . With the help of operations on series one then proves that
for any and Euler's formula
apply to any . The formula follows from this
- ,
which can also be used for the definition of . This formula shows that the set of values of the same , and that this function periodically with periods , .
Therefore its inverse function is ambiguous and defined for all . It can be specified using the formula , where the amount, the set of values of the argument of, and the usual real logarithm are. The main value of this function is obtained by using the main value instead . For real is by the usual definition , so this function on the set agrees with the usual real logarithm.
For any with one then defines:
This is also an ambiguous function, the main value of which results from the use of instead .
But for this ambiguity disappears and the usual powers with whole exponents arise, which were defined in the first section. Be and , then draws the exponential representation
after that
applies.
For a rational exponent with the abbreviated fraction representation , with , the power has exactly different values. This is especially true for . Is odd and , then there is exactly one real number among them, and that is the number from Section 1.3. Is even and , then takes no real values. But if is even and , then the power takes on exactly two real values that have different signs. In this case, the positive one is exactly the same as the number from section 1.3.
As an example, consider the potency high .
Off and
- With
follows
This results in
- With
The main value corresponds and is the same
Special potencies
Integer powers of 10 (powers of ten ) form the basis of our number system , the decimal system . Written as a power, e.g. For example, 10 −9 for 0.000000001 or 10 11 for 100 billion, they are used in the natural sciences to represent very large or very small positive numbers.
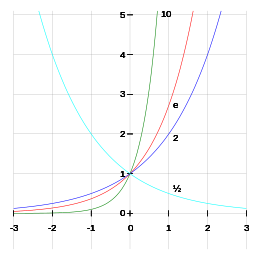
In mathematics and technology, powers with the base , Euler's number, are still particularly important .
Powers of two result from repeated doubling. The surprisingly rapid growth of the numbers makes powers of two popular for practical examples:
- A sheet of paper of usual size can only be about seven to half the size fold . It then has 128 layers and only 128th of its area. If it could be folded 42 times, which is only possible in theory, its thickness of approx. 400,000 km would correspond roughly to the distance from the earth to the moon .
- Everyone has two biological parents and most have four grandparents and eight great-grandparents. Without loss of ancestors , 70 generations ago, at the time of Christ's birth, that would be ancestors , although fewer than 10 9 people lived at that time.
- The wheat grain legend from the inventor of the game of chess, who doubled the number of wheat grains on each square on the chess board, also illustrates the rapid growth of the powers of two.
For digital processing of data on the computer which is the binary system used with the base. 2 The size units of digital storage systems are therefore the powers of two, i.e. the powers of base 2 (that is, 1, 2, 4, 8, 16, ...). A Kibibyte (abbreviated KiB) corresponds to bytes .
In pyramid schemes , such as so-called Schenk circles , some systems are launched, providing not only a doubling, but as an eight-fold increase of new members per step. Such consequences grow so quickly that the systems inevitably collapse after just a few steps. The stability of the pyramid schemes often suggested by the initiators cannot exist. They are therefore banned in many countries for good reason.
Zero to zero
Analysis
The question of whether and in what way an unambiguous value can be assigned to the expression has occupied mathematicians at least since the first half of the 19th century.
The figure on the right shows in its 3D representation of the graph of the function that any values can be achieved through a suitable choice of approximation points to the origin . So is z. B.
- ,
- ,
-
with , and , - and
- .
The examples show that the function diverges at this point , because a limit value of this type obviously does not exist.
An expression that is under the sign of the limit value and that cannot be calculated on the basis of limit value sets and continuity properties is called an indefinite expression . Examples are as well . The latter expression arises from calculations of powers whose base and exponent contradict each other and cannot be determined if there is no relationship between the two.
As a suitable under circumstances obvious value can (which is in the figure, the straight line because of any true) or (the beam because for true) view. But there are also modern analysis textbooks that expressly leave the power (in this form) undefined.
Until the beginning of the 19th century, mathematicians apparently placed their bets without questioning this definition in more detail. Augustin-Louis Cauchy , however, listed together with other expressions as in a table of indefinite expressions. In 1833, Guillaume Libri published a work in which he presented unconvincing arguments for which subsequently became controversial. In defense of Libri, August Ferdinand Möbius published evidence from his teacher Johann Friedrich Pfaff , which essentially showed that applies, and alleged evidence that if applicable, provided. The correctness of this proof was the counterexample and refuted quickly.
Donald E. Knuth mentioned the story of the controversy in the American Mathematical Monthly in 1992 and firmly opposed the conclusion that it is left undefined. If one does not assume the value 1 for the power , many mathematical statements such as the binomial theorem require
special treatment for the cases (at the index ) or (at the index ) or (at ).
Likewise, the power comes in power series such as for the exponential function
for at the index or in the empirical formula for the geometric series
for at the index . Here, too, convention helps .
The cited applications of the power are (like many other similar ones) statements about polynomials, multinomials or power series in which the exponent of the term is constant 0 and the base - rather exceptionally - can take the value 0. In all of these cases, the terms that occur are continuous summands or factors that have the value 1 for invertible items, the value of which can then easily (and completely in the sense of ) be added continuously as 1 for the gap .
Knuth differentiates, however, and writes: “Cauchy had good reason to consider as an undefined limiting form ” (German for example: Cauchy had good reason to consider an undefined Limes expression), whereby he understands limiting form to limit processes of the form Both the base and the exponent for a certain one approach 0 at will.
With this stipulation by D. E. Knuth, the simple cases of the absolute terms in polynomials and power series are solved immediately and in a general way, without conflicting with a detailed consideration of more complicated boundary processes.
Set theory
In set theory, a power of two sets is defined as the set of all functions from to , that is, as a set of sets of ordered pairs , so that for each there is exactly one with . If one denotes the cardinality of , then what justifies the power notation for sets applies (for finite sets, but also beyond). Now there is exactly one function defined on the empty set , that is, a set of pairs with the above property, namely . Therefore , whatever remains right applies .
The natural numbers are defined recursively in set theory as follows (see von Neumann's model of natural numbers ):
Accordingly, in set theory:
Inverse functions
Since the commutative law does not apply to exponentiation, there are two inverse arithmetic operations:
- the extraction of the square root to solve equations according to their design , i.e. to find the basis if the exponent is known,
- taking the logarithm for equations of the type , i.e. determining the exponent when the basis is given.
Generalizations
More general bases
In general there are powers with positive, integer exponents in each semigroup . If this has a neutral element and thus becomes a monoid , then exponent 0 also makes sense and is then always the neutral element. The power laws apply to all
- if and swap, d. H. if applies.
If an element can be inverted , one can use
- For
Define powers with any integer exponent. The calculation rules apply analogously. In the case of abelian groups , it does show that by the potentiation of the structure of a - module is induced.
More general exponents
More general exponents such as matrices are usually only considered in connection with the base , i.e. as values of the generalized exponential function .
In addition, the power notation is occasionally used for other natural continuations. For example, in algebraic number theory, powers of elements of ( topological ) Galois groups with exponents in the completions of are sometimes considered; it is then the uniquely determined continuous continuation of the mapping
For any cardinal numbers and , the power can be defined by, whereby the set of all functions is denoted by primitive set and image set . This generalization presupposes the power set axiom , whereby the axiom of choice is usually also assumed for handling the cardinal numbers .
Ambiguity of the exponent notation
The exponent notation can have different meanings, especially for functions , depending on whether the notation is to reflect the iteration of the concatenation or the point-by-point multiplication. In addition, an upper index could also be meant. As a rule, what is meant is clear from the context.
Concatenation
The power notation is often used as an abbreviation for the concatenation of functions whose values are again within the definition range, for example for iterations in dynamic systems .
One defines, where id denotes the identity on the domain, recursively:
for , so
and so on.
This means for the function values
and general
As an extension of this definition, it is usually defined as the inverse function of . In particular, this notation is also on many calculators , for example, and otherwise is there inverse trigonometric functions with designated. Often also describes the archetype function .
multiplication
As a shorthand notation for the multiplication of several functional values of trigonometric functions with the same arguments as for example with the addition theorems for trigonometric functions occur frequently, has also naturalized potency notation, that is, to write
- .
This is not compatible with the notation presented above for chaining functions. The same applies to polynomials . With one always means the -fold product of the indeterminate with itself. Since the indeterminate as a polynomial function is the identical mapping, the power notation as an iteration of functions would not make sense here.
Superscript
For indexed quantities, the index is sometimes written superscript, so that the formulas give the impression of exponentiation. This occurs particularly in tensor calculus , for example when designating vector fields in coordinate notation , or when indexing quantities that are already indexed, such as sequences of sequences.
Derivation
If the exponent is written in brackets, the corresponding derivative is usually meant, and then denotes the -th derivative of the function .
In programming languages
The notation with a superscript exponent is practical and easy to read in handwritten formulas and in typesetting , but impractical with typewriters and terminals where the characters in a line are all on the same level. Therefore, many programming languages use alternative ways to represent a power:
-
x ↑ y: ALGOL , Commodore BASIC -
x ^ y: BASIC , J , MATLAB , R , Microsoft Excel , TeX (and its offshoots), TI-Basic , bc (for integer exponents), Haskell (for non-negative integer exponents), Lua , ASP and most computer algebra systems -
x ^^ y: Haskell (for rational basis and integer exponents), D -
x ** y: Ada , Bash , COBOL , Fortran , FoxPro , Gnuplot , OCaml , Perl , PHP , PL / I , Python , REXX , Ruby , SAS , Seed7 , Tcl , ABAP , Haskell (for floating point exponents), Turing , VHDL , JavaScript -
x⋆y: APL -
(expt x y): Common Lisp -
x sup y: eqn
In many programming languages there is a corresponding library function instead of a power operator, for example pow(x,y)in C , Math.pow(x,y)in Java or JavaScript and Math.Pow(x,y)in C-Sharp .
Related topics
- Exponential function is a function with a variable exponent, the power function with a variable base.
- Corresponding sequences are the geometric sequence and the power sequence .
- The binary exponentiation is an efficient method for potentiation of natural exponent.
- A power tower is a power whose base and / or exponent is itself a power.
- Order of magnitude , scientific notation - to represent numbers using powers.
Web links
Individual evidence
- ↑ potency. Bibliographisches Institut - Dudenverlag, accessed on June 3, 2016 .
- ↑ Loan translation from Greek δύναμις, dýnamis, which in ancient geometry at least since Plato also had the meaning "square".
- ^ Syntax the Algorithmic Language Algol 60. ( Memento from August 28, 2012 in the Internet Archive )
- ↑ Answer to a question on Stackoverflow about power operators in Haskell
- ↑ erarb. by Günther Reinelt. With assistance from Carsten Kreutz: Lambacher Schweizer - Mathematik für die Fachhochschulreife / [Hauptbd.]. Total band. 1st ed., [Dr.] 1. Klett-Schulbuchverlag, Stuttgart 2008, ISBN 978-3-12-732691-8 .
- ^ Augustin-Louis Cauchy: Analyze algébrique. The table with the indefinite expressions is on page 69.
- ↑ Guillaume Libri: Mémoire sur les fonctions discontinues. Journal for pure and applied mathematics, 10 (1833), pp. 303-316.
- ↑ August Ferdinand Möbius: Proof of the equation , after JF Pfaff. Journal for pure and applied mathematics, 12 (1834), pp. 134-136.
- ^ Donald E. Knuth : Two notes on notation. In: American Mathematical Monthly. Vol. 99, no. 5, May 1992, pp. 403-422 ( preprint on Knuth's website as TeX source text; GZIP ; 26 kB), ( also on arXiv as PDF). The story of the controversy is on page 6 of the preprint.
- ↑ You can see it the other way around - with the same result in the end: The spelling is a "short form" of , which does not contain an exponent 0. It is agreed that the value of a power is to be taken as 1 if its exponent becomes 0 through a constellation of the running variables .
- ↑ Thomas Jech : Set Theory , Springer-Verlag (2003), ISBN 3-540-44085-2 , page 28, equations (3.3)
- ↑ Brian W. Kernighan, Lorinda L. Cherry: Typesetting Mathematics - User's Guide (Second Edition) . August 15, 1978, p. 2 (English, kohala.com ).





















![a ^ {q} = a ^ {{{\ tfrac mn}}}: = {\ sqrt [{n}] {a ^ {m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3f6d9fc9c7bbb967fcd80208480f8fdb6175c52)

![a ^ {{{\ tfrac mn}}}: = ({\ sqrt [{n}] a}) ^ {m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8aa850ce061f6372bc0677657f538c34bbec5946)
![{\ displaystyle 2 ^ {3,1} = 2 ^ {31/10} = {\ sqrt [{10}] {2 ^ {31}}} = ({\ sqrt [{10}] {2}}) ^ {31}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7588047e230a34f745e7522cb9be8d0ccc295ad)







![-2 = (- 8) ^ {{1/3}} = {\ sqrt [{3}] {- 8}} = {\ sqrt [{9}] {(- 8) ^ {3}}} \ neq {\ sqrt [{6}] {(- 8) ^ {2}}} = 2](https://wikimedia.org/api/rest_v1/media/math/render/svg/0be7c43f01ea964b85e5515d3e6bfbc6da736104)












![a ^ {{{\ frac {m} {n}}}} = {\ sqrt [{n}] {a ^ {m}}} = ({\ sqrt [{n}] a}) ^ {m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c27335eba4c1d0546f4d3617c1700aef479f082f)































































![{\ sqrt [{n}] a} = a ^ {{{\ frac 1n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2211e22214f87e6a2303d3d4c2465a3229984bde)













![{\ displaystyle x \ in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)
![{\ displaystyle y \ in [-1, + 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a912e69cc1d811a5fe59d97e6c5e4006e98c438)




























































































