Maple (software)
| Maple
|
|
|---|---|
|
Maple Standard under Xubuntu 16.10 |
|
| Basic data
|
|
| developer | Waterloo Maple Inc. |
| Publishing year | 1982 |
| Current version | 2020 (March 12, 2020) |
| operating system | platform independent |
| programming language | C , Java |
| category | Computer algebra system |
| License | proprietary software |
| www.maplesoft.com/products/maple/ | |
Maple ( ma thematical mani p ulation l anguag e ) is an English-language Computer Algebra System (CAS) for Algebra , Analysis , discrete mathematics , numerical analysis and many other branches of mathematics . It also provides an environment for the development of mathematical programs and enables the visualization of mathematical structures.
history
The first version of Maple was programmed in 1980 by Keith O. Geddes, Gaston H. Gonnet and their staff from the Symbolic Computation Group at the University of Waterloo in the Canadian city of Waterloo, Ontario . At the end of 1987 Maple was already available in version 4.2.
Maple has been developed and marketed by Maplesoft , a division of Waterloo Maple , since 1988 . Waterloo Maple has been part of the Japan-based Cybernet Systems Co., Ltd since September 2009 .
The scientific support of the Maple project was and is about developing fast and efficient algorithms for symbolic calculations and integrating them into the program. In addition to the Ontario Research Center for Computer Algebra (ORCCA), consisting of the Maple Symbolic Computation Group ( University of Waterloo ) and the Symbolic Computation Laboratory ( University of Western Ontario ), scientists at ETH Zurich are or were involved in this work , the Institut national de recherche en informatique et en automatique (INRIA) and many other laboratories worldwide.
Since 1998 there has been a collaboration between Maplesoft and the Numerical Algorithms Group (NAG). NAG components were first found in Maple Release 6 from 2000. These components led in particular to a considerable improvement in computing speed and computational accuracy in the field of linear algebra.
In 2003 there was Maple for Windows CE 2.0 for mobile use on the handheld Cassiopeia A-23g . This was often used in various upper levels.
In 2005, Maple 10 introduced a new document mode ("document mode") within the standard version of Maple. Since then it has been possible to edit Maple inputs in normal mathematical notation. Texts and mathematical symbols can be combined in the same input line.
Maple 13 offered, among other things, significant improvements in the output of 3D graphics , new procedures and new interactive tutors.
From version 14 of Maple it is possible to access worksheets together with other Maple users ( MapleCloud ). You can make your own resources available to all Maple users worldwide or only to members of certain working groups.
Maple 15 differed from the previous versions in particular in that it significantly increased the computing speed of computers that are equipped with several processors .
In addition to new packages (such as GroupTheory ), new arithmetic commands and numerous improvements, Maple from version 17 offers an editor that supports the development of source text with syntax highlighting and other functionalities. In addition, function calls are now processed considerably faster than before thanks to the use of hardware-supported algorithms.
user interface
The main component of the graphical user interface of Maple is the respective worksheet, in which one works interactively. It appears as a window in which arithmetic instructions ( maple inputs ) are entered. The Maple engine interprets these instructions and returns the corresponding outputs ( Maple outputs ).
Typical Maple outputs are numerical values, terms , functions , tables, 2- and 3-dimensional graphics, animation objects and diagrams . It is possible to edit the objects or expressions created by Maple via context-sensitive menus.
Inserting mathematical symbols, expressions , vectors and matrices into arithmetic instructions is made easier by using palettes . These consist of pre-prepared code snippets for various tasks that can be added to the worksheet with a click of the mouse.
From version 9 on there is a Java -based version of Maple Standard in addition to the Classic Worksheet Maple . The standard version of Maple offers a more comfortable interface, but on the other hand it is significantly slower than the classic version. Because of these two variants, there are also two different ways to save worksheets. A distinction is made between standard worksheets ( file extension : mw) and classic worksheets (file extension: mws; compatible with older Maple versions).
A finished worksheet can be exported as a PDF , HTML , LaTeX or RTF document if required .
Packages
Maple comprises a core of frequently used standard arithmetic instructions ( main library ) and additional packages that can be loaded at runtime using the with command . Some of the most important of these over a hundred packages are listed below:
- CodeGeneration (tools for translating Maple source code into other programming languages )
- combinat (for solving combinatorial problems)
- DEtools (for calculating with differential equations )
- DifferentialGeometry (for differential geometry , especially for calculating with Lie algebras and tensors )
- DynamicSystems (for working with linear systems )
- geometry (for two-dimensional Euclidean geometry )
- geom3d (for three-dimensional Euclidean geometry )
- GraphTheory (for graph theory )
- GroupTheory (for calculating with finally presented groups )
- LinearAlgebra (for calculating with vectors and matrices )
- Logic (for the two-valued logic )
- Maplets (for creating graphical user interfaces for Maple)
- NumberTheory (for number theory )
- PDEtools (for solving partial differential equations )
- Physics (for calculations in theoretical physics )
- plots (graphics package)
- plottools (for creating and modifying graphic objects)
- RandomTools (for working with random objects)
- RealDomain (creates a real-valued context)
- ScientificConstants ( physical constants and properties of chemical elements )
- ScientificErrorAnalysis (for error calculation )
- Statistics (for statistics and analysis of data)
- Units (for calculating with (especially physical) units)
- VectorCalculus (for vector analysis )
Interfaces
Maple has interfaces to Matlab , Fortran , C , C # , Java , Visual Basic , Python , Perl , R , JavaScript , Julia and Swift , which translate Maple code into these target languages. Conversely, Fortran, C, C # or Java routines can be integrated into Maple, and Maple can be called from C, Java and VisualBasic (OpenMaple API ).
Application examples
The following are simple examples of arithmetic instructions in typical Maple notation.
- Calculate the square root of 2 to 21 significant digits precision :
RootofTwo:= evalf[21](sqrt(2));
- Solving a quadratic equation :
solve(3*x^2+b*x=7, x);
- Computing the derivative of a function :
f:= x -> tan(x)*sqrt(x): D(f)(x);
- Calculating an indefinite and a definite integral :
int(sin(x)^2, x);
int(sin(x)^2, x = 0..Pi/2);
- Solving a linear differential equation of the second order:
DGL:= diff(y(x),x,x) - 3*y(x) = x:
dsolve({DGL, y(0)=1, D(y)(0)=2}, y(x));
- Calculating the coordinate equation of a sphere :
with(geom3d): sphere(K, [point(M, 2, 3, -2), 3/4]): Equation(K, [x, y, z]);
- Representation of a parameterized area :
with(plots):
tubeplot({[3*t^2, 2.5*t, 0.2*t, t = -4..5, radius = 4]},
numpoints = 15,
tubepoints = 20,
orientation = [-33, 69]);
- Representation of a standing wave :
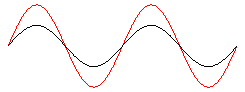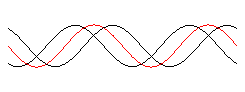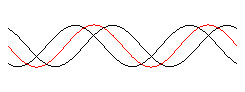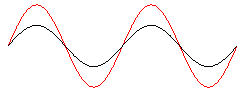
with(plots): y1:= x -> sin(x - 2*Pi*t): y2:= x -> sin(x + 2*Pi*t): defs:= x = -2*Pi..2*Pi, t = 0..1, frames = 150: Wrechts:= animate(y1(x), defs, color = black): Wlinks:= animate(y2(x), defs, color = black): Wres:= animate(y1(x)+y2(x), defs, color = red): display([Wrechts, Wlinks, Wres], axes = NONE);
literature
- Michael B. Monagan et al .: Programming with Maple V , Springer Verlag, 1996, ISBN 978-3-642-61078-3 .
- Maciej Klimek , Grażyna Klimek: Discovering Curves and Surfaces with Maple . Springer, New York 1997, ISBN 978-0-387-94890-4 .
- Hannes Stoppel: Mathematics vividly: bridging course with Maple . Oldenbourg Verlag (2002), ISBN 3-486-25775-7
- Michael Kofler, Gerhard Bitsch, Michael Komma: Maple - Introduction, Application, Reference . Addison-Wesley Longman (2002), ISBN 3-8273-7036-1
- Alexander Walz: Maple 7: Computing and Programming . Oldenbourg (2002), ISBN 3-486-25542-8
- Thomas Westermann: Solving mathematical problems with Maple . Springer Verlag (4th edition 2010), ISBN 3-642-12150-0
- Rüdiger Braun, Reinhold Meise: Analysis with Maple . Vieweg + Teubner Verlag (2nd edition 2012), ISBN 978-3-8348-1573-6
Web links
- Maplesoft
- Ontario Research Center for Computer Algebra (ORCCA)
- Computer Algebra Group (CAG) at Simon Fraser
- dh Materials: Introduction to Maple
- Maple for the blind and visually impaired with information on the use of Maple for the blind and visually impaired
Individual evidence
- ↑ Casio Cassiopeia A-23g Handheld with Maple ( Memento of the original from January 28, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 276 kB); Retrieved December 8, 2012