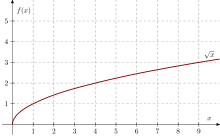
Graph of the square root function

The square root (colloquially root; English square root , just sqrt ) a non-negative number is that (uniquely determined) non-negative number whose square is equal to the given number is. The symbol for the square root is the square root sign , so the square root of the number is represented by. The number or the term under the root is called a radicand . The more detailed notation is less common. In addition, the square root can be expressed as a power : is equivalent to For example, because and the square root of is equal .







![{\ sqrt [{2}] {y}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09a5c859d31b85b7d986e72a6c54f1fa8316031)






Since the equation has for two solutions , the square root is usually defined as the nonnegative of the two solutions; That is , it always applies. This means that the concept of the square root is unique. The two solutions to the equation are thus and




Preliminary note on the definitions
There are two problems to consider when formally defining the square root:
- If you limit yourself to nonnegative rational numbers , then in many cases the square root is undefined. Even in antiquity it was found out that the number, for example, can not be a rational number (see Euclid's proof of the irrationality of the root of 2 ).

- In general, there are two different numbers whose squares match a given number. For example, the number would also be a possible candidate for the square root .



The symbol for the square root was first used during the 16th century . It is believed that the character is a modified form of the lowercase r , which is an abbreviation for the Latin word "radix" (root). Originally the symbol was placed in front of the radicand; the horizontal extension was missing. Even Carl Friedrich Gauss therefore used brackets for more complicated root expressions and wrote, for example, instead of

In English, the square root is called "square root", which is why the term "sqrt" is used for the square root function in many programming languages .
Square roots of real numbers

Graph of the square function (red and blue). By reflecting only the blue half at the bisector of the 1st quadrant, the diagram of the square root function (green) is created.
Definition: The square root of a nonnegative real number is the nonnegative real number whose square is equal .





Equivalent to this, the real square root can be defined as a function: Let

the (bijective) restriction of the square function to the set of nonnegative real numbers. The inverse of this function is called the square root function

Remarks
- It should be noted that the square function explained by is defined for all real numbers, but is not reversible. It is neither injective nor surjective .

- The constraint of the square function is reversible and is reversed by the real root function. Since only nonnegative real numbers appear as images of , the real root function is only defined for these numbers.


- Because of the restriction made before the inversion from to nonnegative real numbers, the values of the square root function are nonnegative numbers. Restricting the square function to other subsets of , in which different real numbers always have different squares, would lead to other inverse functions, but these are not called real square root functions.


Examples
Square numbers and their square roots
| Radicand |
square root |
|
Radicand |
square root
|
| 1 |
1 |
121 |
11
|
| 4th |
2 |
144 |
12
|
| 9 |
3 |
169 |
13
|
| 16 |
4th |
196 |
14th
|
| 25th |
5 |
225 |
15th
|
| 36 |
6th |
256 |
16
|
| 49 |
7th |
289 |
17th
|
| 64 |
8th |
324 |
18th
|
| 81 |
9 |
361 |
19th
|
| 100 |
10 |
400 |
20th
|
Properties and rules of calculation
The properties of the square root function result from the properties of the square function restricted to the set of non-negative real numbers:
-
 for .
for .
-
 for .
for .
-
 , d. i.e., the square root function is strictly increasing.
, d. i.e., the square root function is strictly increasing.
-
 holds with the real amount for any real numbers .
holds with the real amount for any real numbers .
- In contrast, only applies to non-negative .


- The square root function is differentiable , there applies .


- At the point 0 it is not differentiable, its diagram has a perpendicular tangent with the equation .

- It can be Riemann-integrable on every closed subinterval of its domain , one of its antiderivatives is .
![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

Calculating square roots from real numbers
Rational (approximate) values of
some square roots
|

|
Even if the square root of a natural number is to be taken, the result is often an irrational number , the decimal fraction expansion of which is therefore a non-periodic, non-terminating decimal fraction (namely precisely when the result is not natural). The calculation of a square root, which is not a rational number, therefore, is to determine an approximate value sufficient accuracy. There are a number of ways to do this:
- Written rooting
- This is an algorithm similar to the common method of written division.
- Interval nesting
- This procedure is quite easy to understand, albeit very cumbersome in practice.
- Example (approximate value for ):

- From and it follows that lies between 1 and 2. Therefore you try , etc. From and you can see that it must be between 1.4 and 1.5. Continuing this procedure with more and more decimal places finally delivers an approximate value with the desired accuracy:









-
Babylonian root pulling or Heron method
- This iteration method is often used when programming the calculation of the roots for calculators because it converges quickly . It is Newton's method of finding zeros applied to the function .

-
Taylor series development
- The Taylor series expansion of the root function with an expansion point can be used as a Taylor expansion of around the point as a binomial series





- be found because this series for pointwise to converge . With that results



-
 For
For 
- Calculation using the CORDIC algorithm
- This process is mainly used in calculators, FPUs and microcontrollers .
Determination of the square root graphically
One possibility is the Kathetensatz : The number whose square root is sought, is on a number line of coated out. A semicircle with a radius is drawn over the distance between and ( Thales circle ). At , a perpendicular to the baseline is established that intersects the semicircle (height of a right triangle). The distance from this point of intersection to the zero point is the square root of (cathetus).







Square roots of complex numbers

The extraction of the roots corresponds to bisecting the angle in the complex plane. Example:

If a complex number other than zero, then the equation has


exactly two solutions for , also known as the roots or square roots of . These lie in the Gaussian plane of numbers on the two points of intersection of the circle around 0 with the radius and the bisector of the angle between the rays emanating from or through . The one of the two roots that lies in the right half-plane is called the principal value of the root. For negative (real) values , the root with the positive imaginary part is the main value.







If you write the complex number in the form


where and are real with and , then the following applies to the principal value of the root:





The second square root value (the secondary value) results from point reflection (180 ° rotation) at the zero point:

definition
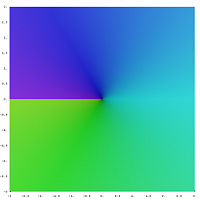
The complex function “ square z ”, like the real square function, does not have an inverse function because it is not injective , but unlike real numbers it is surjective, that is, every complex number is the square of a complex number. Analogous to the real (non-negative) square roots, one can therefore define complex square root functions by restricting the domain of definition to a subset of the complex numbers on which is injective and remains surjective. Depending on which subset you choose, you get different branches of the square root function as the inverse.




The main branch of the complex square root function results if one considers the domain of

is based on, this is the right half plane of the complex number plane , whereby only the numbers with nonnegative imaginary part belong from the edge . The restriction of to is a bijective mapping of to to the complex numbers, so its inverse function, the main branch of the square root of to, is entirely defined. The value of this inverse function is called the principal value of the square root of . If by a specific complex number is meant, then it is that main value.








Is given in Cartesian coordinates, i.e. with real numbers and , then results





for the main value of the square root, where the function has the value −1 for negative and the value 1 otherwise (also for and thus different from the sign function ):





The only side branch of is

Is in polar coordinates given with , the main value of the square root of


![\ arg (z) \ in (- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b49f881e0c5973f5c7738a22d3b33b9a21d78558)

where is the real (nonnegative) square root of . The secondary value results again as .



The magnitude of the two roots is therefore the root of the magnitude of the complex number. For the main value, the argument ("the angle of z ", see below) is halved. The other solution results geometrically by point reflection of this main value at the origin .

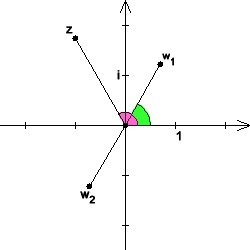
The argument of a complex number is the oriented angle in the complex plane of numbers , which are points and in real coordinates. In the example below, the argument from and the argument from are highlighted in color.







- Complex square root
A branch of the square root
Example: Computing a complex square root
Find the square roots of First, the amount of the radicand is determined:


This gives the main value of the square root to
![{\ displaystyle {\ begin {aligned} w_ {1} & = {\ sqrt {\ tfrac {2 + (- 1)} {2}}} + \ mathrm {i} \ cdot \ operatorname {sgn ^ {+} } ({\ sqrt {3}}) \ cdot {\ sqrt {\ tfrac {2 - (- 1)} {2}}} \\ [0.3em] & = {\ sqrt {\ tfrac {1} {2 }}} + \ mathrm {i} \ cdot (+1) \ cdot {\ sqrt {\ tfrac {3} {2}}} = {\ sqrt {2}} \ cdot \ left ({\ tfrac {1} {2}} + \ mathrm {i} \ cdot {\ tfrac {1} {2}} {\ sqrt {3}} \ right) \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c65fbfa85729505faa6fa18dff479108b517c08c)
The other root is obtained by reversing the sign:

Power law
The power law

does not apply to everyone , not even to the main values of the roots.
This can already be seen in the special case resulting
from the further specification



who because of identity too


can be simplified, according to which apparently every negative number provides a counterexample, for example :

- Because of and the main value of has the argument , while the main value of has the argument .






- Remarks
- Since principal values of roots from positive radicands must be positive, the counterexample shows that there cannot be a square root function for which the power law applies to all .


- For and any one can freely choose the “sign” of two of the three roots, after which exactly one possibility remains for the “sign” of the last third.



Square roots modulo n
Square roots can also be defined in the remainder class ring . Analogously to the real and complex numbers, a square root of is called if:




However, one has to use different methods to calculate square roots modulo than to calculate real or complex square roots. To find the square roots of modulo , one can proceed as follows:



First you determine the prime factorization

of the module and then the solutions modulo of the individual prime powers . These solutions are finally put together to form the desired solution using the Chinese remainder theorem .


Calculation of square roots modulo a prime number p
The case is simple: Because of and modulo 2, every number has a uniquely determined square root, namely itself. For prime numbers not equal to 2, the square roots of :





To test whether it even has a square root in , one computes the value of the Legendre symbol

-
 ,
,
because it applies:

In the first case there is no square root in and in the second case it only has the square root 0. The interesting case is the third case, and therefore we assume in the following that it holds.



Calculation for the case p mod 4 = 3
If the Legendre symbol is 1, then are


the two square roots of modulo .


Calculation for the case p mod 4 = 1
If the Legendre symbol is 1, then are


the two square roots of modulo . Here one chooses so that




applies. You can simply test different values of . The consequence is recursively through



Are defined.
Sample calculation for and :


According to the above formula, the square roots of through are


given. For one finds the value by trying , because the following applies:



The values for and result as follows:



Substituting these values gives

That means: 15 and 22 are the two square roots of 3 modulo 37.
Square roots from matrices
As the root of a square matrix is any matrix , which multiplied by itself result:




As with the square root of real or complex numbers, the square root of matrices is not necessarily unique. However, if one only looks at positively definite symmetric matrices, then the formation of the roots is unambiguous: Every positively definite symmetric matrix has a positively definite symmetric root which is clearly defined.It is obtained by diagonalizing with the help of an orthogonal matrix (this is always possible according to the spectral theorem ) and then replaced the diagonal elements with their roots; however, the positive root must always be chosen. See also Cholesky decomposition . The uniqueness follows from the fact that the exponential mapping is a diffeomorphism from the vector space of the symmetric matrices to the subset of the positively definite symmetric matrices.



Square root of an approximate integral operator
You can numerically approximate the specific integral function from 0 to with and a given function , which assumes the values at the equidistant interpolation points , as a matrix multiplication as follows (for ):










It is vividly clear that one can repeat this operation and thus obtain the double integral :


So one can understand the matrix as a numerically approximated integral operator.

The matrix cannot be diagonalized and its Jordanian normal form is:


To get a square root from it, one could proceed as described for the non-diagonalizable matrices. However, there is a more direct formal solution in this case as follows:

with , and .



The indices denote the subdiagonals (0 is the diagonal) and the exponent is equal . If one assumes real and positive, then real and by definition is positive.





With this one can numerically approximate a "half" certain integral from 0 to the function as follows:




If you are looking for all operators which, when multiplied by themselves , result in the approximate integral operator , you also have to insert the negative sign, that is, there are two solutions .


To derive the formula, you can first invert, raise the result to the power and then invert it again.


See also
Web links
supporting documents
-
↑ The validity of the power law for square roots is not assumed in the quoted passage, but is sometimes assumed in the literature (for negative real radicands): Klaus Fritzsche: Tutorium Mathematik für Einsteiger . Springer-Verlag, 2016, ISBN 978-3-662-48910-9 ( limited preview in Google Book Search [accessed July 4, 2017]).







![{\ sqrt [{2}] {y}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09a5c859d31b85b7d986e72a6c54f1fa8316031)



































![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


















































![\ arg (z) \ in (- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b49f881e0c5973f5c7738a22d3b33b9a21d78558)














![{\ displaystyle {\ begin {aligned} w_ {1} & = {\ sqrt {\ tfrac {2 + (- 1)} {2}}} + \ mathrm {i} \ cdot \ operatorname {sgn ^ {+} } ({\ sqrt {3}}) \ cdot {\ sqrt {\ tfrac {2 - (- 1)} {2}}} \\ [0.3em] & = {\ sqrt {\ tfrac {1} {2 }}} + \ mathrm {i} \ cdot (+1) \ cdot {\ sqrt {\ tfrac {3} {2}}} = {\ sqrt {2}} \ cdot \ left ({\ tfrac {1} {2}} + \ mathrm {i} \ cdot {\ tfrac {1} {2}} {\ sqrt {3}} \ right) \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c65fbfa85729505faa6fa18dff479108b517c08c)








































































